基于FPGA的FPMSM滑模观测器无传感器控制

王明义，杨贵杰，赵品志

(哈尔滨工业大学，黑龙江哈尔滨150001)

0引 言

随着功率器件、现代电力电子技术和控制理论的发展，由逆变器供电的电机可以摆脱三相电网对电机相数的束缚。同三相电机相比，多相电机具有功率密度高、力矩波动小、效率高、可容错控制等优点，在要求低压高功率输出、高可靠性等应用场合，多相电机的使用得到人们广泛的关注［1-2］。在多相电机驱动系统的研究中，人们致力于容错控制、脉宽调制算法、注入谐波对电机性能变化等方面的研究［3-5］，而在多相电机无传感器控制方面研究较少，但多相电机与无传感器控制都具有高可靠性和高鲁棒性［6］，本文将多相电机的无传感器控制作为研究重点，对五相永磁同步电动机无传感器控制进行研究。

滑模控制由于具有对参数变化不敏感、对外部扰动的鲁棒性和动态响应快等优点，广泛应用在电机控制中。本文通过对五相永磁同步电动机(以下简称FPMSM)模型的分析，建立滑模观测器位置估算模块，输入基波电压和基波电流估算转子角度。在基于FPGA的System Generator开发平台上，采用模型系统级设计方法，实现了滑模观测器位置估算仿真，并通过实验验证了该方法的有效性。

1 FPMSM数学模型

本文所研究的电机为表贴式FPMSM，它具有绕组正弦分布和转子永磁体正弦磁场分布特性。为分析方便，假设FPMSM特性如下［7］:

(1)忽略磁路饱和、磁滞现象和涡流损耗;

(2)转子永磁磁体在气隙中产生的磁势为正弦分布，无高次谐波;

(3)定子绕着加对称五相正弦电流时，只产生正弦分布的磁势，忽略高次谐波;

(4)电机隐极结构，交直轴电抗相等，即Ld=Lq。

1．1 FPMSM在a-b-c-d-e坐标系下数学模型

定子电压方程:

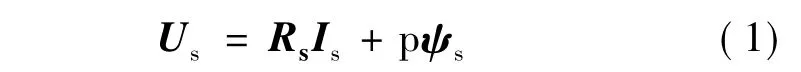
定子磁链方程:

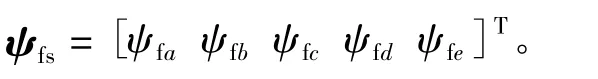
1．2 FPMSM 在 α1-β1-α3-β3-O 坐标系下数学模型

a-b-c-d-e坐标系到 α1-β1-α3-β3-O坐标系变换矩阵为:

α1-β1-α3-β3-0坐标系下电压方程:

式中:Uαβ0=TUs=［uα1uβ1uα3uβ3u0］T;Iαβ0=TIs

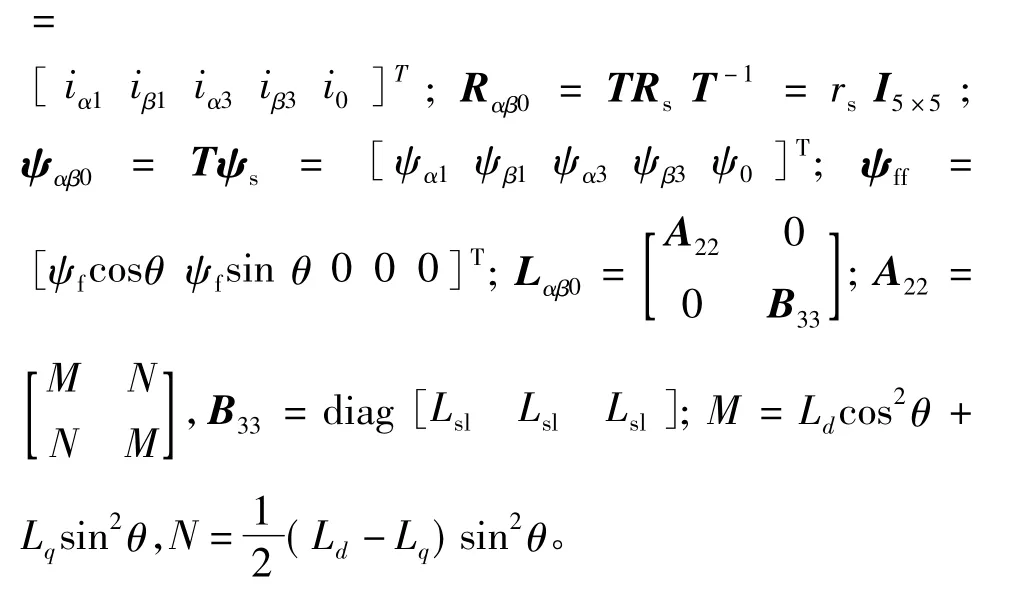
本文电机为表贴式FPMSM，Ld=Lq=Ls。则A22简化:

式中:C21= ［-ψfωrsin θ ψfωrsin θ 0 0 0］T。

式(7)中前两行基波方程中存在反电势:

将式(7)整理为:

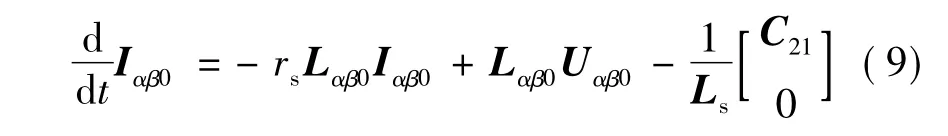
式(9)前两行可以表示:

由式(3)可知，电机位置与反电势有关，通过估计反电势就可以得到转子位置信息，本文利用基波反电势进行转子位置估算。

2基于滑模观测器转子位置估算

FPMSM模型的滑模观测器状态方程:

通常滑模观测器采用高频开关函数，但是由于开关时间和空间上的滞后，使滑模观测器抖振现象严重，无法在工程中实践，本文采用饱和函数作为控制函数，使观测器具有较强的鲁棒性，削弱抖振现象［8〛。

式中:Δ为饱和区间临界线，k为滑模增益，此系数需满足可达性和存在性，观测器才能进行滑模运动。

采用滑模观测器对电流进行估计，其滑模超平面选择:

由式(9)和(14)可得滑模观测器动态方程:

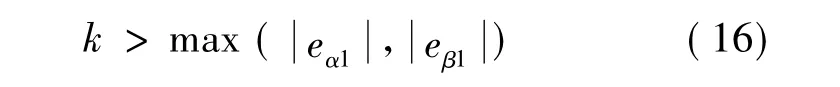
根据等效控制原理，可以得到:

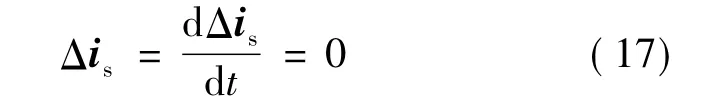
由式(15)和式(17)得到估算反电势:

反电势估算值在α1-β1轴的分量可求得转子转角估算值:

3滑模观测器的SG/Simulink仿真

FPGA作为当代高性能信号处理的理想器件，具有高速并行运算的能力，它不仅包含查找表、寄存器、多路复用器，而且嵌入了快速乘法器、加法器，因此，FPGA在图像处理、数字通信等领域得到了广泛的应用。System Generator(SG)可以作为开发FPGA的设计方式，具有集灵活性、高效性和直观性于一身的优点［9］，其利用Xilinx公司的IP核构建相应数学模块，这些模块搭建的系统模型经过仿真验证后可以生成Verilog HDL，缩短了FPGA开发时间。本文利用SG建立滑模观测器部分，FPMSM和SVPWM等其他部分用Simulink搭建，利用Gateway模块实现两者无缝连接。

3．1滑模观测器的SG建模

图1为滑模观测器的转子转角估算模块，其组成部分包括滑模电流观测器、滤波器、转角补偿等部分。估算过程为把电流观测器得到的估算电流与定子电流实测值输入给控制函数，输出控制变量Zs，Zs经过滤波处理后得到Zss，利用Zs和Zss估算反电势es，通过es分量计算角度估算值，最后加入角度补偿等到转子角度θ。

根据以上原理，分析得到SG构建FPMSM的滑模观测器位置估算模型，其中输入FPMSM定子基波电流 iα1、iβ1，基波电压 uα1、uβ1，速度 ω，输出为估算角度θ，如图2所示。

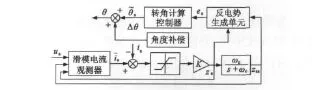
图1 滑模观测器模块图

图2 SG构建的滑模观测器模型

3．2 仿真结果

为了验证以上估算策略的正确性，本文利用Simulink搭建了FPMSM矢量控制模型。利用SG搭建了滑模观测器模块，仿真得到估算位置、估算定子电流、估算反电势等波形。

仿真用电机参数选取为定子相电阻Rs=4 Ω，定子基波相电感Ld1=Lq1=45 mH，定子三次谐波相电感Ld3=Lq3=5 mH，电机极对数p=1，电机转动惯量 J=0．8 ×10-6kg·m2。在负载转矩为 0．5 N·m，电机转速为800 r/min的情况下进行仿真。

转子转角实际值和估算值波形如图3所示。可以看出，基于SMO的转子转角估算值与转子转角的真实值基本一致。

图3 转子转角仿真波形

α1-β1坐标系下实际和估算电流的仿真波形如图4所示。估算电流在滑模面上作滑模运动，与实际电留幅值和相位基本一致，由于滑模观测器固有的抖振现象，因此估算电流出现抖振。

图5为控制函数输出控制变量波形。反电势es被包容于控制变量Zs中，因此利用滤波器得到估算反电势。

4 FPGA实现及实验结果

为验证SG设计SMO模块的正确性，实验平台是以XC3S1200E为核心的控制系统，电机为实验室内部设计的FPMSM，电机参数如表1所示。

表1 实验电机参数

将SG设计的滑模观测器生成Verilog HDL代码嵌入到FPMSM控制程序中，利用XC3S1200E的IO口将估算的位置信号输出，通过调节滑模系数k、临界区间Δ等参数，输出了与实际位置相匹配的估算位置，如图6所示。图7为电机实际转速与估算转速波形。电机为开环起动，结果表明，估算转速能很好跟踪实际转速，抖振现象微弱。

由实验可知，在电机转速为510 r/min时，利用SG建模设计的SMO模块可以很好地估算出FPMSM的位置信号，说明可以利用 FPGA开发FPMSM滑模观测器无传感器控制的可行性。

图6 转子实际角度、估算角度实验波形

图7 转子实际转速与估算转速波形

5结 语

本文通过对FPMSM模型分析，建立了电机的滑模观测器位置估算模型，并在观测器中使用了饱和函数来削弱抖振，通过加入角度补偿方式，减少了滤波器带来的角度偏差。利用SG搭建了滑模观测器模块，经过仿真验证了此方法的正确性。实验证明此方法是可行的，减少了利用FPGA开发FPMSM无位置控制的开发周期。

［1］ EMIL L．Multiphase electric machines for variable-speed applications［J］．IEEE Transactions on Industrial Electronics，2008，55(5):1893-1909．

［2］ Singh G K．Multi-phase induction machine drive research a survey［J］．Electric Power Systems Research，2002，61(2):139-147．

［3］ Nicola B，Silverio B．Strategies for fault toler ant current control of a five-phase permanent-magnet motor［J］．IEEE Transactions on Industry Applications，2007，43(4):960-968．

［4］ 赵品志，杨贵杰，刘春龙．五相电压源逆变器SVPWM优化算法［J］．电机与控制学报，2009，13(4):516-522．

［5］ Arahal M R，Duran M J，Barrero F．Stability analysis of five-phase induction motor drives with variable third harmonic injection［J］．Electric Power Systems Research，2010，80(12):1459-1468．

［6］ De Belif F M L，Mel J A．Application of a voltage adaptive sensorless current controller to multi-phase PMSM［C］//International Symposium on Advanced Electromechanical Motion Systems and E-lectric Drives Joint Symposium，2009:1-6．

［7］ Yu Fei，Zhang Xiaofeng，Qiao Minzhong．The direct torque control of multiphase permanent magnet synchronous motor based on low harmonic space vector PWM［C］//IEEE International Conference of Industrial Technologies．2008:1-5．

［8］ 鲁文其，黄文新，胡育文．永磁同步电电动动机新新型型滑模观测器无传感器控制［J］．控制理论与应用，2009，26(4):429-432．

［9］ 吴平仿，吴定会，纪志成．SVPWM的SG设计及FPGA实现［J］．微特电机，2006(10):26-19．