电传动车辆用永磁同步电动机快速控制原型仿真

刘春光，马晓军，曾庆含

(装甲兵工程学院，北京100072)

0引 言

内置式永磁同步电动机(以下简称PMSM)具有较高的功率密度和过载能力，而且易于弱磁扩速，适合用作电传动履带式车辆的牵引驱动。

在车用PMSM的控制中，电机在恒转矩区和弱磁区采取不同的控制结构和控制算法，不仅系统结构复杂，工作模式判断算法复杂、切换不平滑，而且不能全局范围内通过磁场对电流进行定向，电机瞬态响应不是最优。本文作者在文献［1］中提出了一种基于磁链规划曲线对定子电流进行定向控制的方法，即将定子磁链规划为转速的函数，任意转速下根据给定的磁链确定定子电流控制分量，以获得最优的瞬态响应。

实际上，履带式电传动装甲车辆运行工况复杂，其电驱动系统是一个时变、非线性、强耦合系统，逆变器、电机等部件特性复杂，建模困难，给调速系统中控制器参数设计和调整带来困难，难以快速验证控制算法的有效性和控制效果。为此，本文基于dSPACE软硬件平台，构建了一种适用于PMSM的快速控制原型仿真系统，代替真实控制器嵌入电机试验台架，对控制算法进行了实时仿真验证。试验结果表明:该系统能够进行多种运行工况的电机控制试验，控制系统快速、无差地跟踪速度给定信号，避免了恒转矩控制和弱磁控制的变结构切换问题，实现电机平滑调速，验证了上述算法的正确性和有效性。

1基于磁链规划的定子电流控制

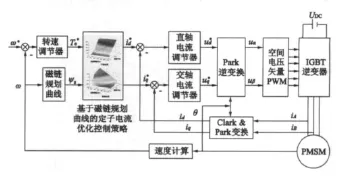
图1 基于磁链的定子电流控制的矢量控制原理框图

图1为基于磁链的定子电流控制的矢量控制原理框图。该系统采用转速、电流双闭环控制，外环为速度环，转速调节器根据转速给定与反馈的误差输出转矩期望;内环采用电流环，相电流经滤波、坐标变换后的直、交轴电流分量(id，iq)作为电流反馈，电流调节器输出经空间电压矢量控制模块生成PWM控制信号，控制逆变器开关器件的通断。与一般双环调速系统不同的是，控制器采用基于磁链规划曲线的定子电流优化控制策略，由转矩期望与规划磁链共同计算定子电流直、交轴电流的控制量(，)，在全转速范围内进行统一的定子电流定向控制，避免了恒转矩区和弱磁区的控制结构与算法的切换。

1．1全局范围内的磁链归一化

无论在恒转矩区还是弱磁区内，对于任意转速下的给定转矩，总对应唯一的电流分量(id，iq)与定子磁链值ψs，满足:

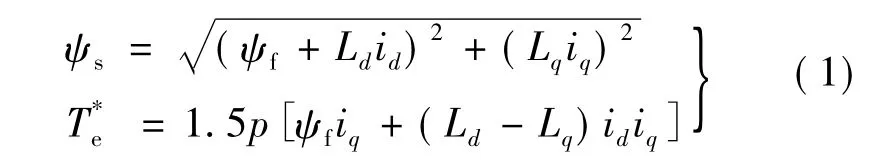
因此，可对全速范围内定子磁链进行归一化处理，由磁链规划曲线和给定期望反解电流控制给定值。

为尽可能地拓宽恒转矩区运行范围，全速范围内磁链规划曲线可表示:

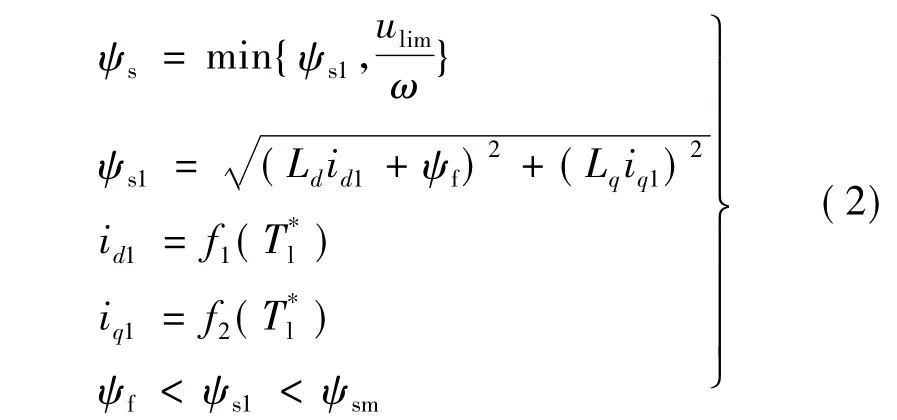
图2为定子磁链与转速之间的规划曲线图，恒转矩磁链(水平直线)与弱磁磁链曲线的交点，即恒转矩区与弱磁区两种工作模式之间的分界点。由于磁链规划曲线是连续的，基于式(1)计算定子电流分量时，系统由恒转矩运行自然过渡到弱磁运行状态，改变了恒转矩区和弱磁区之间进行判断与切换的控制结构，保证工作模式的平滑过渡。

图2 全速范围内的磁链规划曲线图

1．2基于磁链规划曲线的转矩优化控制算法实现

为使系统具有最优的动态响应，本文采用基于磁链规划的最优转矩控制的定子电流算法任意转速下，结合转矩期望动态确定磁链规划值，计算磁链规划值下电机的最大输出转矩值:

(1)若转矩期望大于最大输出能力，则电机按照最大输出能力曲线进行控制。

(2)若转矩期望小于最大输出能力，则由磁链规划椭圆与期望转矩曲线的交点确定定子电流分量。

图3为基于磁链规划曲线的转矩优化控制算法流程图。实际上，无论按照最大转矩输出能力曲线，还是根据定子磁链与转矩期望来确定电流分量，直、交轴电流的解析式都非常复杂。在实际的应用中，借助MATLAB软件进行计算，通过神经网络训练形成以磁链、转矩为输入，以电流分量为输出的计算模型，如图4所示。在各种运行工况下，均可以通过查表获取电流控制分量。

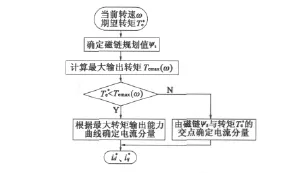
图3 转矩优化控制算法流程图

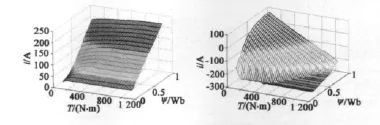
图4 定子电流计算模型

2基于dSPACE的驱动系统快速控制原型实时仿真

dSPACE系统是由德国dSPACE公司开发的一套基于MATLAB/Simulink的控制系统开发的工作平台，本文将其作为控制器原型连接实际的被控对象，构成半实物仿真系统，可在线调整控制器参数，快速验证和观测算法的控制效果。

2．1驱动系统半实物仿真总体结构

图5为基于dSPACE的电传动车辆驱动系统半实物仿真原理图。它主要由三部分构成:逆变器和电机以实物形式出现在闭环中，省去了复杂的建模过程，并采用真实的电传动车辆操纵装置输入控制给定，完全模拟控制器应用环境;MATLAB软件、RTI接口和Control Desk虚拟试验软件等被装在dSPACE宿主机上，以完成控制器功能设计、算法调试，软硬件接口联接以及代码生成、下载等功能;基于磁链的优化转矩控制算法被下载在dSPACE处理器中，通过DS2202的丰富接口采集电机转速、三相电流，并输出PWM控制信号，经过驱动电路提供实际的开关信号驱动逆变器进而控制电机调速。

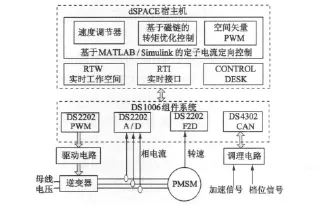
图5 基于dSPACE的驱动系统半实物仿真原理图

2．2控制算法实时仿真模型

快速控制原型仿真的核心是建立控制器实时仿真模型，目的是在线调整控制器参数，快速验证控制算法。在MATLAB/Simulink环境下，基于磁链的定子电流定向控制的实时仿真模型如图6所示。

仿真模型主要包括dSPACE系统的I/O接口和控制算法两部分。

图6 基于磁链的定子电流定向控制的实时仿真模型

(1)I/O接口模块:配置DS4302的CAN通信模块，采集操纵控制器分配给右侧电机的加速信号，作为控制给定。采用DS2202的4路并行AD实时转换接口，得到三相电流 ia、ib、ic和母线电压 VDC。通过DS2202F2D接口对增量式光电码盘输出脉冲的采集，转速/位置模块解算出当前电机转子位置θ与转速 n。空间矢量脉宽调制信号经过DS2202PWM接口送外围驱动电路。

(2)控制算法模块:速度调节器输出转矩期望，并根据磁链规划曲线查表计算当前允许磁链。转矩优化模块根据上述算法计算得到直轴、交轴电流分量的控制给定，经过电流调节以及电压前馈控制，得到交直轴控制电压，再经过空间矢量PWM模块计算逆变器上桥PWM控制信号。

3实时仿真试验与分析

实验用牵引电机参数:PN=100 kW，ψf=0．296 Wb，Ld=1．332 ×10-3H，Lq=3．966 ×10-3H，Rs=0．4 Ω，电机极对数 p=4，母线电压 VDC=750 V。

图7、图8分别为采用本文提出的基于磁链规划的控制算法与传统的变结构矢量控制时转矩、转速响应曲线的对比图。实验给定目标转速200 rad/s，电机带200 N·m负载起动。采用传统的变结构矢量控制时，在0．6 s时电机转矩由最大值1 080 N·m突降至300 N·m并出现明显振荡回升，2．4 s后进入稳定弱磁状态，相应地，电机转速在转矩波动过程中上升缓慢，进入稳定弱磁状态后实现扩速，2．8 s达到200 rad/s。其中转矩、转速响应波动是由恒转矩区向弱磁区切换时控制结构和算法的变换引起的，这与理论分析一致。采用本文提出的基于磁链规划的转矩优化控制后，1．2 s时由恒转矩区自然过渡到弱磁区，转矩变化平滑并远大于传统弱磁控制下的转矩输出能力，系统动态性能明显优于传统控制算法。

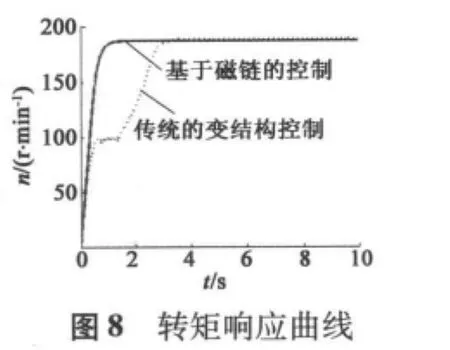
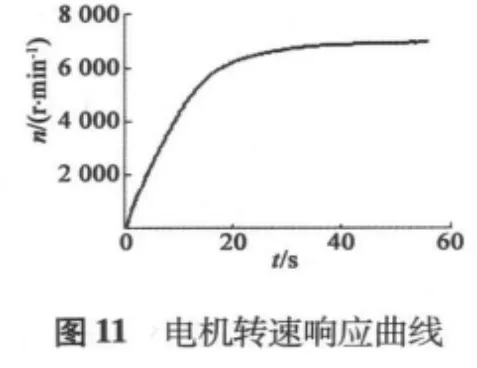
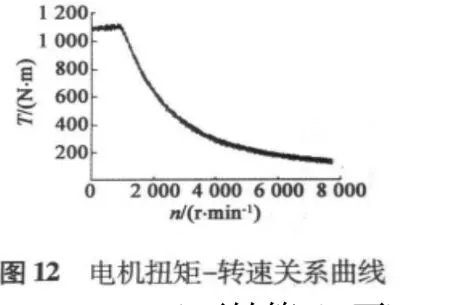
图9、图10分别为电机带180 N·m负载起动过程中直、交轴分量变化曲线以及转速响应曲线。低速时，电机恒转矩运行，电流分量id=-186．4 A、iq=232．5 A基本保持恒定;随转速增加进入弱磁区后，直轴电流id进行弱磁，而后在磁链规划曲线的作用下自动进行转矩优化控制，电流减小，而交轴电流持续减小，直到最后稳定运行。图11、图12分别为加速过程中电机转速响应曲线和转扭-转速关系曲线。可见，电机转速平稳上升，电磁转矩波动较小，实现了恒转矩区和弱磁区之间的平滑过渡。

实验结果表明，采用本文提出的基于磁链的定子电流定向控制算法，有效解决了PMSM在弱磁区和恒转矩区控制切换的难题，算法简单，运行稳定。

4结 语

在常规的履带式电传动车辆用电驱动系统的控制中，通常在恒转矩区和弱磁区采用不同的控制算法，系统调速过程中需要进行变结构切换，切换过程中转矩脉动较大。本文首次提出一种基于磁链规划曲线的定子电流定向控制算法，在全速范围内根据磁链规划曲线和转矩期望确定直交轴电流分量，进行电机转矩优化控制和平滑调速，并借助于dSPACE和相关物理部件进行了快速控制原型仿真。结果表明该控制算法有效解决了上述问题，具有良好的控制效果，同时，为实际控制器的开发打下了基础，为驱动控制系统的设计和开发提供了新思路和方法。

［1］ 刘春光．基于多平台联合的电传动装甲车辆建模与仿真研究［D］．装甲兵工程学院，2008．

［2］ Enrico C．Design of solar high altitude long endurance aircraft for multi pay load＆ operations［J］．Aerospace Science and Technology，2006(10):541-550．

［3］ Alexander R．Diagonally implicit Runge-Kutta methods for stiff O．D．Es［J］．SIAM Journal on Numerical Analysisi(S0036-1429)，1977，14(6):1006-1021．

［4］ 卢子广．电力驱动系统实时控制虚拟实验平台［J］．中国电机工程学报，2003，23(4):119-123．