基于灰色马尔科夫链模型的交通量预测
刘宗明,贾志绚,李兴莉
(太原科技大学1.电子信息工程学院;2.交通与物流学院;3.应用科学学院,山西太原030024)
利用道路交通量调查资料对未来交通量进行合理准确的预测是决策部门制定发展规划的重要依据[1]。灰色系统理论具有所需样本少,不需要计算统计特征量等特点。灰色系统理论在预测方面应用十分广泛,如电力负荷的灰色预测,城市噪声的灰色预测,以及自然灾害的灰色预测等。近些年来,交通领域的科研人员,也将灰色系统理论引入并应用交通系统的某些部分,比如在城市交通生成总量预测、道路交通流量预测,城市道路交通噪声预测,铁路货运量预测和公路客运量预测等方面。在交通量的预测方面国内科研人员也做了相应的研究[2-8],主要有灰色经济学模型,交通量演变模式检索方法,灰色残差GM(1,1)模型以及一些改进的灰色模型等。
灰色马尔科夫模型是一种结合灰色系统理论和马尔科夫链的理论的预测模型。首先灰色预测方法用于预测变化趋势较为明显的时间序列,对随机波动性大的时间序列则效果不是太好,马尔科夫链的理论适用于随机过程的状态转移行为,正好可以弥补灰色预测的局限,但马尔科夫链的预测对象要求具有平稳过程、等均值的特点,交通系统的变化多属于非平稳过程,如果采用GM(1,1)模型拟合系统,并在此基础上对随机波动大的残差序列进行马尔科夫预测,实现两者优势互补。运用灰色马尔科夫预测模型进行对太原市某街道15 min交通量进行预测,结果表明,该模型在交通量预测方面具有很好的精度。
1 建模
利用灰色马尔科夫预测建模过程如下:即先用灰色GM(1,1)对原始数据进行建模,在此基础上对残差进行GM(1,1)建模,然后结合马尔科夫链理论根据残差符号建立状态转移概率矩阵。
1.1 建立原始数据的GM(1,1)的预测模型

式中:a,u为待辨识的参数。
解该微分方程为

由最小二乘法求解待辨识的参数a,u表示为

式中Y和B为
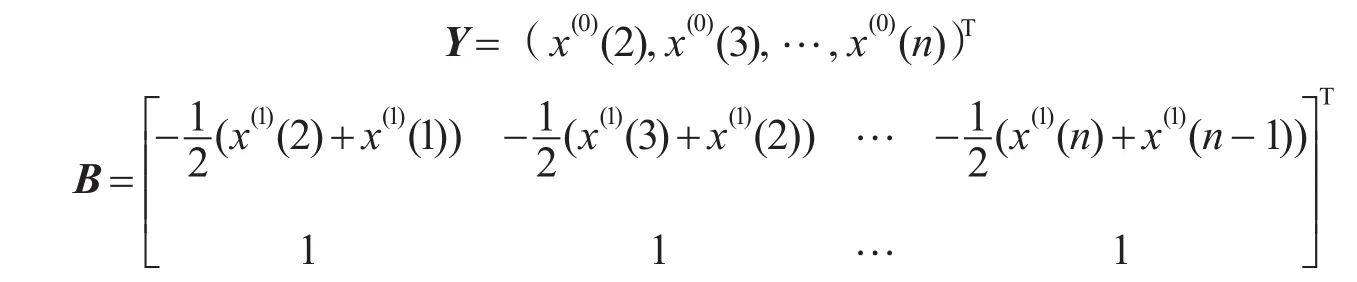

由于

因此得到原始数据模型值为

1.2 建立残差绝对值序列的GM(1,1)模型
由上面的分析得到残差绝对值序列为


式中:u1,a1为待辨识的参数。
得到的微分方程为

由最小二乘法求解待辨识的参数a,u,估计值a,u,系数,Y1和B1如下式

得到改进后的原始数据的预测值为

式中:符号函数
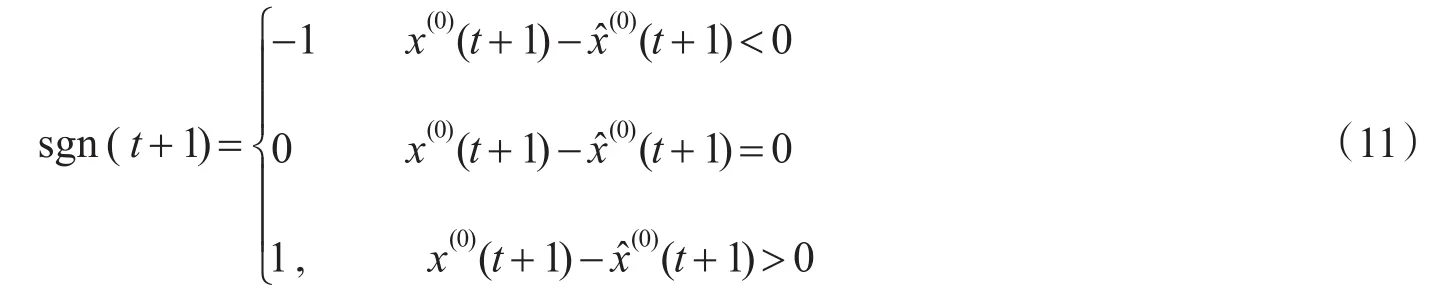
由上面的分析可知,1≤t≤n时,sgn(t)的值可由原残差的符号确定,因此提高灰色预测精度的关键是正确预测t>n时sgn(t)值的概率。
根据马尔可夫理论,对于时间和状态都是离散的马尔科夫过程,称为马尔科夫链,马尔科夫的过程是研究系统的状态及状态的转移,即状态转移概率。由状态转移概率组成马氏链的转移概率矩阵如下

本文用马尔科夫过程来求解残差状态转移的概率,从而确定计算预测值时残差的符号,这里确定3种状态,残差为零时状态取为1,残差为正时状态取为2,残差为负时状态取为3,然后构建状态转移概率矩阵。
2 应用实例
以太原市漪汾桥断面为例,实地调查其交通量数据,从早7:00-9:30,每15分钟作为一个调查时间单位,测得交通流量数据如表1所示。

表1 交通量数据表Tab.1 Data of traffic volume
取表1中时间段7:00-9:00的数据作为原始数据,取9:00-9:30时间段的两组数据作为预测数据对照值,令X(0)(t)={503,558,630,637,702,622,861,676}建立灰色的马尔科夫链预测模型,步骤如下:
累加序列:{X(1)(t)}={503,1 061,1 691,2 328,3 030,3 652,4 513,5 189}
构造矩阵B和向量Y:

由最小二乘法求得

通过计算得到模型值及残差如表2所示。

表2 模型值及残差值Tab.2 Value of model and residuals
通过该模型得到的结果如表3所示:

表3 模型值及残差值Tab.3 Value of model and residuals
根据原始残差的符号残差符号状态划分如表4所示。
由表2中残差的符号状态构建转移概率矩阵:

通过以上得到预测模型预测时间段9:00-9:30的交通量,结果如表5、6所示,可以看出:灰色马尔科夫链预测模型交通量的预测精度较高,相对误差较小。
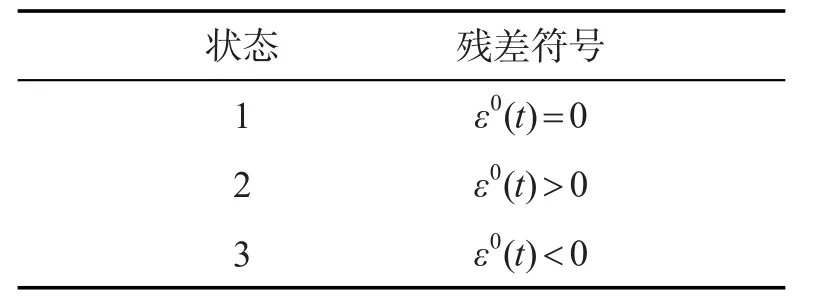
表4 状态划分表Tab.4 Status partition

表5 GM(1,1)结果表Tab.5 Results of GM(1,1)

表6 灰色马尔科夫链模型结果表Tab.6 Results of Gray-Markov Chain model
4 结论
1)灰色马尔科夫链模型是一种结合灰色系统理论和马尔科夫链的理论的预测模型,在此基础上,通过对原始数据的序列和残差绝对值序列二次建立GM(1,1)预测模型,引进马尔科夫链的状态转移概率矩阵建立了交通量预测模型。
2)当预测长期交通量时,可以根据已有的历史数据,重新选取原始数据进行建模,然后重构马尔科夫链的状态转移概率矩阵,达到长期预测的目的。
3)结合太原市漪汾桥断面的实际交通量数据,建立了其交通量预测模型,研究结果表明:与灰色GM(1,1)模型相比,相对误差明显减小,该模型在交通量预测精度上有了很大的改进。
[1]STEPHEN C.Traffic prediction using multivariate nonparametric regression[J].Journal of Transportation Engineering,2003,129(2):161-168.
[2]徐冲,孙晓燕,王海龙,等.灰色经济计量学模型在交通量预测中的应用[J].公路工程,2010,35(5):34-38.
[3]靳引利.基于交通量演变模式检索的高速公路交通量预测方法[J].公路交通科技,2010,27(1):116-121.
[4]陈淑燕,陈家胜.一种改进的灰色模型在交通量预测中的应用[J].公路交通科技,2004,21(2):81-83.
[5]周荣康,徐永,李若灵.基于灰色残差GM(1,1)模型的道路交通量预测的研究[J].交通运输工程与信息学报,2008,21(3):49-53.
[6]孙燕,陈森发,周振国.灰色系统理论在无检测器交叉口交通流量预测中的应用[J].东南大学学报,2002,32(2):256-258.
[7]严磊.基于灰色理论与神经网络的交通量组合预测模型研究[D].重庆:重庆大学.2010:32-37.
[8]许伦辉,傅惠.交通信息智能预测理论与方法[M].北京:科学出版社,2009:135-142.

