土钉支护强度比与类粘聚力关系试验研究
喻晓今
(华东交通大学土木建筑学院,江西南昌330013)
对边坡基坑临空面附近土体的力学性质有许多研究。关于土压力理论,主要还是在朗肯土压力和库仑土压力理论上的发展与调试;关于土体的强度,主要还是以屈斯卡、广义屈斯卡、米泽斯、广义米泽斯和莫尔-库仑等等理论为基础;而土体稳定性则以塑性力学的极限理论等为主要的依据[1-2]。对于边坡基坑工程的稳定性评价,有关方法都基于一定的假定,建立某种实体模型,故适于某些应用范围。文[3]更具体地列举了以下主要几种方法的特点,例如:瑞典圆弧法,以滑弧块体为对象,适于某些软弱淤泥地基;Terzaghi法,采用土体竖直条分,其稳定性系数被广泛性应用,偏于安全,误差不超过15%;Bishop法用于近圆弧对象,考虑土条两侧推力时,分条数不宜过大;Janbu法适于任意形状滑动面,竖直条分;Sarma法评价各种破坏模式下的边坡的稳定性,条块的分条是任意的;Morgenstern-Prise法要求垂直条分滑体,充分考虑条间作用力,计算过程比较复杂;Spencer法用于圆弧破坏稳定性,等宽条分等等。从中可见,土体稳定性研究采用平面应变问题假定,最危险的滑弧、滑裂面一般过坡脚,综合了力、力矩平衡理论,即涉及土体的应力、抗剪能力的分析等因素。文[4]将边坡位移细分过程计算,未提出新参数。文[5-6]争论焦点在Mohr-Coulomb强度准则与统一强度理论的本质是继承还是发展的看法上。文[1-14]未发现土钉支护后全面仿照纯土体的参数的概念的演绎。
为寻找土钉支护工程中简便分析方法,同时又使概念清晰,用于探讨土钉支护后的土体对于破裂时的数据与土工参数的对应规律,以小尺度试验为根据,提出土钉支护后的有关混合体的力学性质参数,以确定土钉支护强度比与有关参数的比值关系,具体是土钉支护强度比与类粘聚力、类破裂角的关系。
1 土钉支护试验及数据整理
利用现场原位土体进行试验,试验场地是挖掘直立面坡脚,土钉支护采用击入钉方式。利用地表水平面超载模式,加载采用逐级加载,直至土体破裂,试验土体侧面视图见图1。土体共进行了7次试验。其中3 次无支护加载试验,用以测定土体的物理力学性质,定性对比试验效果的可靠性,其余用于土钉支护试验,以确定相应条件下的土钉支护参数与土体力学性质的对应关系,如强度比B与超载值q、滑裂面水平长度d、滑裂面高度H等等参数的变化规律。

表1 试验参数在破裂时所得数据Tab.1 Data of parameters of experiment at fracture
2 类土体参数的提出和计算
鉴于土体在土钉支护后,其相应的抗压、抗剪强度等土工指标比不加支护者将有较大改变。为了使支护前后的有关参数既有实际意义又有可对比性、取得对这种比较的定量结论,避免误读误解,这里借用土体物理力学性质的已有概念,在已有名词的基础上,定义新的适用于土钉支护后土体对应的物理力学性质参数,即将描述纯土体的参数推广于土钉支护后的土体,为与原来的参数区别,在原参数名称的前面冠以“类”字,参数符号右上标为“*”。
这样,对应于土体的破裂角度αf、内摩擦角φ、朗肯主动土压力系数Ka、粘聚力c、单位面积主动土压力pa等,分别提出支护土体滑裂虚线与水平线夹角为类破裂角度、类内摩擦角φ*、类朗肯主动土压力系数Ka*、类粘聚力c*、类单位面积主动土压力pa*等。另外,滑裂的临界深度(高度)写为z0,即等于H,见图2,图中h、e分别表示超载和滑裂体的重力中心与滑裂线(虚线)的交点之距离超载地面高度和该点距临空面水平距离。
试验现象表明,滑塌体几乎接近三角楔,呈体内破坏形式。为计算便捷,视滑塌体为一整体,看超载和滑塌体的重力中心与正侧面的滑裂线的交点,认为此点的强度等参量可代表整体状态,考察此处大主应力与类粘聚力c*的比值与强度比、类破裂角度的关系。
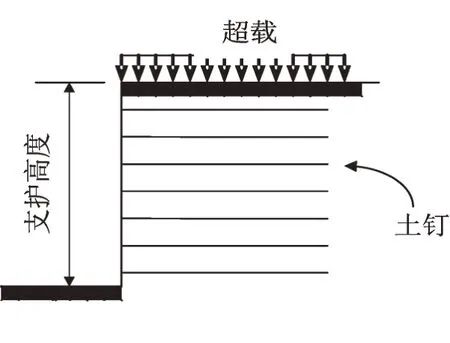
图1 土钉支护立坡简图Fig1. Straight slope of soil nailing
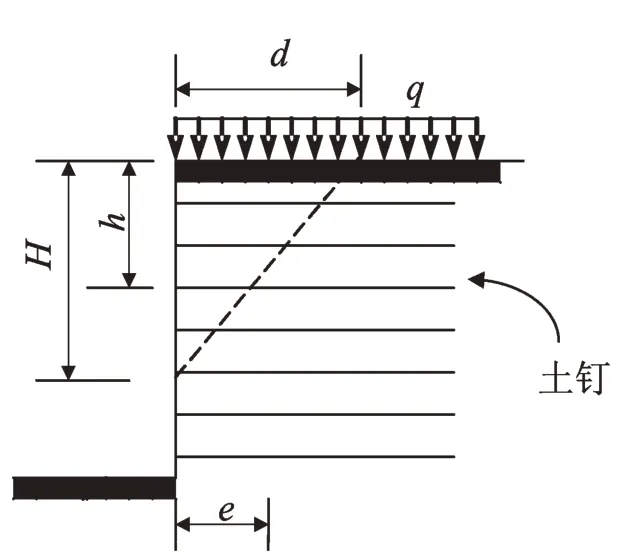
图2 土钉支护滑裂图Fig2. Slipping fracture of soil nailing supporting
这里土体的滑塌采用朗肯主动土压力假定来分析,求解滑裂高度以其理论中存在超载的情形进行计算,即滑裂面的高度H是由土压力大于零处而确定的。据此,以下便是土体钉后相应类力学性质参数数据的计算步骤:① 按三角形滑楔体计算类破裂角度,即以滑裂面水平长度与滑裂面高度确定滑裂线与水平线的夹角;② 按公式φ=2(αf-45°)计算类内摩擦角φ*;③ 以公式Ka=tan2(45°-φ/2)计算类朗肯主动土压力系数Ka*;④ 按临界深度公式计算类粘聚力c*;⑤ 计算超载和滑裂体的重力中心与滑裂线交点处的土压力,公式是pa=(q+γ·z)Ka-2c,z值取h;⑥ 计算大主应力σ1=σ3tan2(45°+φ/2)+2c·tan(45°+φ/2)。按以上步骤的计算结果见表2。

表2 试验类参数计算结果Tab.2 Computing results of experimental parameters
3 强度比等参数关系的拟合
测取、计算有关试验数据后,进行数据的多元线性回归拟合,模型为y=b0+b1x1+b2x2,令其中y为大主应力与类粘聚力之比σ1/c*,x1为强度比B,x2为类破裂角。得到的回归方程为
σ1/c*=-6.016+0.162B+0.146
4 土钉支护实例回归值与定义值
文[8]中基坑为直立面,坑深9.0 m,土钉支护设计参数为:土钉水平和垂直间距分别为SH,SV,SH=SV=1.5 m,土钉钢筋为4 Φ 28,土体重度是18 kN·m-3,地面超载为50 kPa,支护工作正常。按一般稳定安全系数取1.2 计,取坑深失稳深度与正常支护深度比值为1.2,预计其在现状时的破裂线高度H,则得H=10.8 m,按以上类参数定义的计算步骤和公式进行计算,并按回归公式算得该例有关参数的有限个取值见表3。

表3 土钉支护实例的计算值与回归值的比较Tab.3 Comparison of computing values and regression values of a case
5 结论
1)适应土体在土钉支护后的变化,借用土工参数,扩展为“类”参数,既说明问题,又不被误解。以朗肯主动土压力假定来分析计算陡坡基坑土钉支护的类物理力学参数、存在超载的情况求解滑裂高度时,其滑裂面的高度H是对应土压力等于零处的临界深度,找到了类粘聚力c*等参数用于描述被支护土体。
2)若以相同重度、不相同超载的土钉支护土体实例计算结果而论,在γ约为18 kN·m-3,φ约为24°的粉砂质土条件时,本试验结果的大主应力与类粘聚力的比值、强度比、类破裂角之间关系的回归值对应实例中的破裂角为80°的情形,可以回归公式来作为土钉支护预期破裂数据的依据之一。
[1]陈希哲.土力学地基基础[M].4版.北京:清华大学出版社,2004:188-234.
[2]李广信.高等土力学[M].北京:清华大学出版社,2004:114-174.
[3]佴磊,徐燕,代树林.边坡工程[M].北京:科学出版社,2010:64-85.
[4]董建华,朱彦鹏.地震作用下土钉支护边坡永久位移计算方法研究[J].工程力学,2011,28(10):101-110.
[5]余文龙.关于“非饱和土抗剪强度及土压力统一解”的讨论[J].岩石力学,2011,32(4):1278.
[6]张常光,赵均海.对“关于‘非饱和土抗剪强度及土压力统一解’的讨论”的答复[J].岩石力学,2011,32(4):1278-1280.
[7]陈肇元,崔京浩.土钉支护在基坑工程中的应用[M].北京:中国建筑工业出版社,1997:16-25.
[8]段立平,李海深.考虑土拱效应的土钉墙内部竖向平均应力分析[J].路基工程,2011(1):111-113.
[9]曾鲜明,林润德,易平.基坑与边坡事故警示录[M].北京:中国建筑工业出版社,1999:4-97.
[10]喻晓今.土钉瞬态应力动力特性对比研究[J].合肥工业大学学报,2007,30(11):1505-1508.
[11]苏立君,李彦龙,殷建华.土的剪胀性及灌浆压力对土钉抗拔强度影响的数值分析[J].西安建筑科技大学学报,2011,43(4):480-485.
[12]李平,郭佳陇,高德清.基坑坑壁土钉支护技术应用研究[J].路基工程,2011(4):28-30.
[13]YU XIAOJIN. Studies of structural parameters of soil nailing support on steep slope[C]//The Second International Symposium on Innovation and Sustainability of Modern Railway. Irkutsk,Russia:Irkutsk State Transport University,2010:260-269.
[14]喻晓今,余学文,张豫.数种情形下土钉的瞬态应变累积效应分析[J].华东交通大学学报,2006,23(4):1-4.

