永磁同步电动机调速系统的离散滑模控制

杨朋松，孙秀霞，董文瀚，孙 彪，赵云雨

(1.空军工程大学，陕西西安710038;2.94136部队，宁夏银川750000)

0 引 言

由于以永磁同步电动机(以下简称PMSM)为执行部件的高性能调速系统容易受系统参数变化和外界干扰的影响，因此难以采用PID方法实现满意的调速和定位性能［1］。滑模变结构控制是一种鲁棒控制方法，它的滑动模态物理实现简单，且使系统在受到摄动及外干扰时均具有不变性［2］。滑模变结构控制理论在PMSM控制系统中的应用引起了人们的广泛关注，并取得了不少研究成果［3－6］。

随着计算机控制技术和PMSM在工业领域的广泛应用，研究离散滑模控制技术及其在PMSM中的应用显得极其必要。然而，离散滑模控制技术在PMSM控制系统中的应用研究相对较少。文献［7］设计基于内模控制和离散时间趋近律控制的PMSM传动系统，消弱了系统性能对电机模型精度的敏感性，达到了较好的传动性能。文献［8］提出了离散积分趋近律变结构控制策略，并应用于PMSM位置伺服系统，在电机内部参数摄动和外部参数扰动下，该控制策略提高了系统的鲁棒性，实现了精确跟踪并且提高了系统动态性能。然而文献［7］和文献［8］所设计的离散滑模控制器均存在不同程度的抖振，这对机电系统十分有害。

本文提出了一种新的离散滑模控制方法，并应用于PMSM调速系统之中，实现了良好的速度跟踪能力和对电机参数摄动及外干扰的强鲁棒性。通过引入幂次函数，消除了系统的抖振;通过引入一步延时干扰估计实现对干扰的补偿。仿真和实验验证了所提方法的优越性。

1 PMSM数学模型

PMSM的定子和普通电励磁三相同步电动机的定子相似。在建模及分析、设计过程中常作以下假设:转子永磁磁场在气隙空间分布为正弦波，定子电枢绕组中的感应电动势也为正弦波;忽略定子铁心饱和，认为磁路为线性，电感参数不变;不计铁心涡流与磁滞损耗;转子没有阻尼绕组。

在以上假设下，建立d－q坐标系下的PMSM数学模型，其电压方程:

磁链方程:

对于表面式PMSM，有Ld=Lq=L，所以转矩方程:

机械运动方程:

式中:ud、uq为 d、q 轴的电压;id、iq为 d、q 轴的电流;Ld、Lq为d、q轴电感;R为定子电阻;p为电机极对数;ψf为永磁体与定子交链的磁链;Te为电磁转矩;TL为负载转矩;J为转动惯量;B为粘滞系数;ω为转子机械角速度。

采用id=0的PMSM转子磁场定向控制，根据式(1)和式(2)可得:

选取状态变量x1为电机转速x1=ω，状态变量x2为q轴电流x2=iq，控制u为q轴定子电压u=uq，由式(3)～ 式(5)得:

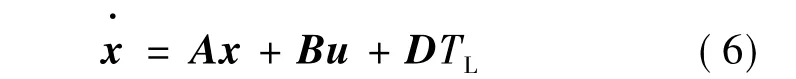
在电机工作过程中会产生热量，定子绕组的电阻会随温度的升高而变大，所以当R变化时，PMSM的模型应为:

由于电机转速、电机的交轴电流、定子电阻变化和负载干扰都是有界的，故令:

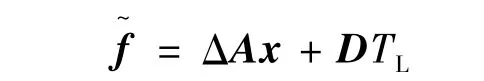
取采样周期为T，采用零阶保持器，将式(8)离散化可得:

控制目标:在电机参数摄动和负载干扰作用下，针对式(9)设计离散滑模控制器，使电机转速能较好地跟踪参考转速，并且系统不存在高频抖振。

2 离散滑模控制器设计

2.1 幂次函数

幂次函数 fal(s，α，δ)是一种非线性函数［9］，利用它可以产生许多智能性的功能，其表达式:

式中:0＜δ＜1。

2.2 滑模控制器的设计

2.2.1 滑模面函数的选择

设电机的参考转速信号为rref(k)，取离散线性切换函数:

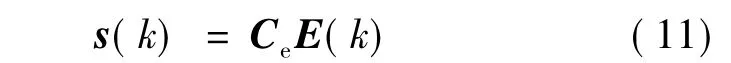
2.2.2 离散滑模控制器设计

引入幂次函数，考虑离散趋近律:

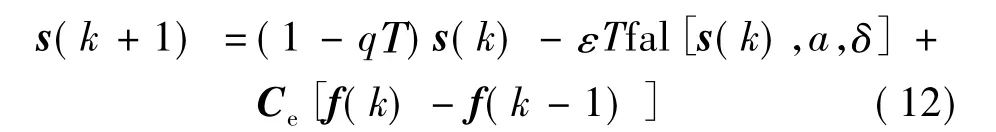
式中:f(k－1)=x(k)－Φx(k－1)－Γu(k－1)，称为一步延时干扰估计［10］。

由式(14)的表达式可以看出，控制量中不含有未知项，是可执行的控制律。

3 系统鲁棒性研究

定理:对于式(9)，在式(14)控制量的作用下，切换函数s(k)无抖振、单调的收敛于原点的某个区域，区域的界是与干扰估计误差有关的某一数值，且系统不存在高频抖振现象。以下进行定理证明。

令干扰估计误差:

式(12)化简:

针对式(12)，分析滑模面s(k)的运动趋势。

(1)0≤Df＜ qΤδ+εΤδa时

(a)s(k)≥δ时，式(15)化为:

设 Δs(k)=s(k+1)－s(k)，得:

对式(17)两边求s(k)的导数:

由Δs(k)≤0知，s(k)递减。故当s(k)≥δ，s(k)递减，直到进入0≤s(k)＜δ的范围。

(b)0≤s(k)＜δ时，式(15)化为:

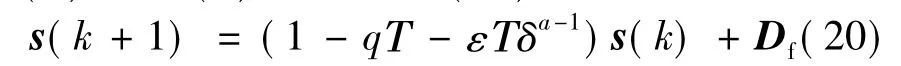
对于式(20)，有:

对于式(21)，有:

(c)s(k)≤－δ时，式(15)化为:

针对式(22)，有:

对式(23)两边求s(k)的导数为:

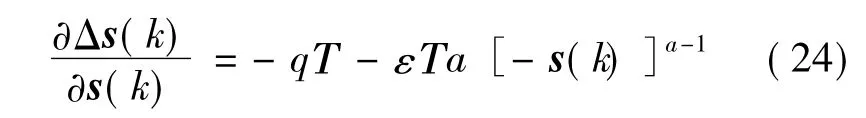
由Δs(k)＞0，可知s(k)递增。故当s(k)≤－δ时，s(k)递增，直到进入－δ＜s(k)＜0的范围。

两组患者治疗前的各项指标无显著差异(P<0.05),而在治疗后组间差异存在统计学意义(P<0.05),详情见表2。

故当－δ＜s(k)＜0时，s(k)递增，直到进入s(k)≥0的范围，由上文推导可知，一旦s(k)进入s(k)≥0的范围，函数s(k)将单调收敛于h1。

(2)Df≥qΤδ+εΤδa时

(a)s(k)＜0时，由式(21)和式(25)可知Δs(k)＞0，s(k)递增。故当s(k)＜0时，s(k)递增，直至进入s(k)＞0的范围。

假设s(k)=h2使得式(26)成立，由减函数的性质可知:

s(k)＜h2时，Δs(k)＞0，s(k)递增;

s(k)=h2时，Δs(k)=0，s(k)不变。

故s(k)≥δ时，函数s(k)单调收敛到h2，且不会出现穿越s(k)=h2现象。

(4)当Df≤ －qΤδ－ εΤδa，同理可得，函数 s(k)单调收敛到s(k)=h4(s(k)=h4使得 －qΤs(k)+εΤ［－s(k)］a=－Df成立)，且不会出现穿越h4的现象。

上述分析结论可知，切换函数s(k)无正负交替、单调收敛于与干扰估计误差相关的某个数值，且不会出现穿越现象，这就从根本上避免了系统高频抖振现象的发生。定理得证。

通过定理的证明可知，式(14)的控制律在系统受到未知有界干扰时可以保证滑模面函数s(k)单调收敛到原点的某个邻域，即系统状态在滑模面的某一邻域内作准滑模运动，且准滑模带宽与干扰估计误差有关。

4 仿真分析

PI控制器参数 Kp=0.08，Ki=0.2。

本文算法与PI控制进行仿真对比研究，仿真结果如图1～图4所示。

(1)突加负载情况

在t≥2 s时加入TL=1 N负载，本文方法和PI控制进行仿真比较研究，仿真结果如图1和图2所示。

图1 PMSM调速系统的转速对比

图2 PMSM的电压输入

(2)参数摄动情况

负载为零时，在时间t≥2 s时，电机的电阻发生摄动变为2R，本文方法和PI控制进行仿真比较研究，仿真结果如图3和图4所示。

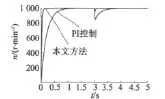
图3 PMSM调速系统的转速对比

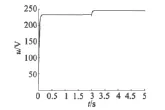
图4 PMSM的电压输入

由图1和图3可以看出，与传统PI控制方法相比，本文方法设计的PMSM调速系统具有较快的响应速度，并且对外界干扰和参数摄动具有较强的鲁棒性。由图2和图4可以看出，本文所设计的控制系统的电压输入不存在高频抖振。

5 实验研究

本文采用TMS320LF2407A芯片作为核心构建实验平台，对一台实际电机进行实验研究。给定转速 n=1 000 r/min，在 t=3.6 s时突加负载，实验结果如图5所示。

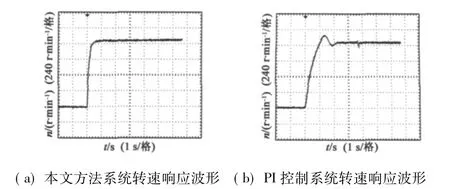
图5 系统转速响应波形

在电机实际运行中，电机绕组电阻随着温度升高会发生一定的变化，电机受到负载干扰时，电机自身的惯性能够克服一部分负载干扰的影响，加上电力电子器件开关滞后等因素的影响，实际电机转速响应与仿真中会有不同。由图5可知，PI控制器控制下的系统，转速响应较慢，有一定的超调，并且对突加负载的鲁棒性较差，本文方法设计的调速系统，转速响应较快，略有超调，对突加负载有较好的鲁棒性。

6 结 语

本文提出了一种新的离散滑模控制方法，并应用到PMSM的调速系统中，实现了良好的速度跟踪能力和对电机参数摄动以及外部干扰的强鲁棒性;控制电压输入不存在高频抖振，消除了传统离散滑模控制中的抖振对机电系统的危害。仿真和实验均验证了该控制器的控制效果。

［1］ 孙强，程明，周鹗，等.新型双凸极永磁同步电机调速系统的变参数 PI控制［J］.中国电机工程学报，2003，23(6):117 －123.

［2］ 刘金琨.滑模变结构控制MATLAB仿真［M］.北京:清华大学出版社，2005.

［3］ Lai C K，Shyu K K.A novel motor drive design for incremental motion system via sliding mode control method［J］.IEEE Trans.on Industrial Electronics，2005，2(52):499 －507.

［4］ 李鸿儒，顾树生.基于神经网络的PMSM自适应滑模控制［J］.控制理论与应用，2005，3(22):461 －464.

［5］ 贾洪平，贺益康.永磁同步电机滑模变结构直接转矩控制［J］.电工技术学报，2006，21(1):1 －6.

［6］ 汪海波，周波，方斯琛.永磁同步电机调速系统的滑模控制［J］.电工技术学报，2009，9(24):71－77.

［7］ 葛宝明，郑琼林，蒋静坪，等.基于离散时间趋近律控制与内模控制的永磁同步电动机传动系统［J］.中国电机工程学报，2004，11(24):106 －111.

［8］ 瞿少成，孟光伟，姚琼荟.PMSM位置伺服系统的离散积分变结构控制［J］.电机与控制学报，2003，2(7):136 －139.

［9］ 韩京清.自抗扰控制技术［M］.北京:国防工业出版社，2008.

［10］ Young K D，Utkin V I，Ozguner U.A control engineer＇s guide to sliding mode control［J］.IEEE Trans.on Control Systems Technology，1999，7(3):328 －342.