基于频率响应法评估油纸绝缘微水含量

刘 君，韦 国，周利军，王 鑫，吴广宁，朱毅刚，张 云

(1. 西南交通大学电气工程学院，成都 610031；2. 惠州电力局，惠州 516001)

油浸式变压器是目前超高压、特高压输变电系统中主变压器的唯一选择，油纸绝缘中微水严重影响变压器绝缘的电气寿命和机械寿命[1]，对投运变压器油纸绝缘的微水状态进行准确评估一直是业内广泛关注的技术难题.变压器绝缘纸微水状态检测分为化学法和电气法．化学法主要指 KFT(Karl Fischer Titration)法，由于无法获取投运变压器绝缘纸的试样，只能通过测量油中的微水来判断绝缘纸中的微水状态，如 Fabre-Pichon曲线、Oommen曲线等[2]，但变压器内部温升的时变性与分布不均匀性导致微水稳态分布曲线评估法误差.电气测试法包括传统测试法(如绝缘电阻测量、介质损耗正切测量等)和电介质响应法．传统测试法局限于单个信息，所受的干扰因素多，无法建立变压器油纸绝缘的微水状态与测试结果的对应关系．电介质响应法作为一种新的绝缘测试方法，其研究始于20世纪80年代，90年代后回复电压法[3]、极化去极化电流法[4]等时域电介质响应法陆续涌现，而频率响应法由于所获信息量大、测试电源电压低而受到广泛关注[5-6]．频率响应法是在宽频范围内(如 10-4～106，Hz)测试油纸绝缘复介电常数实部ε′，虚部(介电损耗)ε′曲线，通过分析其幅值、形状的变化趋势来评估油纸绝缘所处温度、微水含量、老化程度等绝缘状况[7]．

对电介质响应法的研究，目前还处在起始阶段．Saha等[3]通过RVM测试研究了变压器绝缘状态与电介质响应的关系，Gubanski等[8]用 FDS法研究了现场变压器的电介质响应情况，并尝试用介质响应评估油纸绝缘中的微水状态[9-10]．由于其机理复杂，用电介质响应法评估绝缘需要更多的验证[11-13]．

在此基础上，笔者对电介质响应法进行了分析建模，测试了不同微水含量、不同温度条件下油纸复合绝缘 10-4～106，Hz范围频率响应，通过最小二乘法拟合油纸绝缘频率响应与微水含量及温度的关联关系，结果表明，拟合曲面与实验结果基本一致，能有效评估油纸绝缘微水含量及其所处温度，为频率响应法评估油纸绝缘状态及其故障诊断奠定了基础．

1 频率响应测试原理

假设如图1所示的平板电容，两端施加时变电压V(t)，将产生空间均匀电场 E(t)＝V(t)/d，电极两端产生的电势移由自由空间电荷及惯量延迟的极化电势组成[14]，即

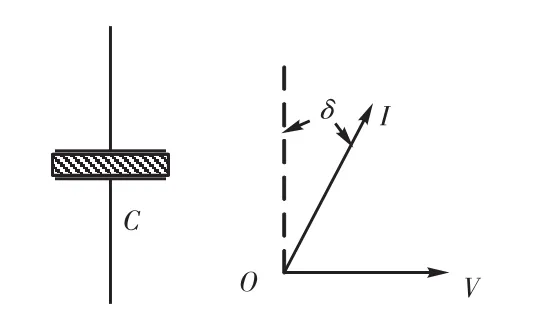
图1 填充电介质的平板电容器Fig.1 Plate capacitor filled with dielectric

如图 2所示，设 f(t)为一介质响应函数，时变场E(t)可视为一系列场强为E(t)dt的δ函数连续叠加，则在 t时刻，系统介质响应 P(t)则为响应 f(τ)E(tτ)dτ在时间从 τ退至负无穷或是激励信号加上的时刻的积分的总和[15]．于是得

式中 ε∞为介质高频下的相对介电常数，代表介质的快速极化．由于 f(t)＝0，(t＜0)，则积分下限可至负无穷，这就是 f(τ)与 E(t)的卷积积分．式(2)的傅里叶变化为

其中，频率相关的极化系数 χ(ω)定义为介质响应函数的傅里叶变换，即

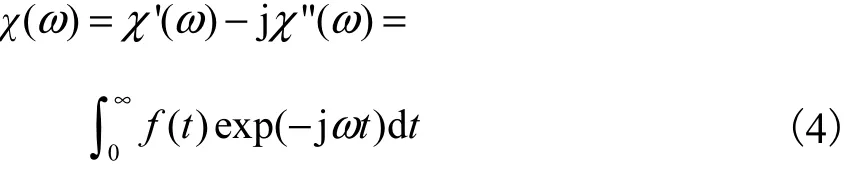
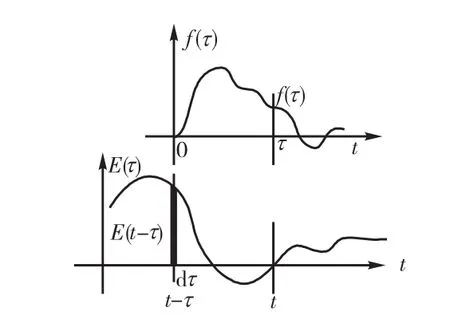
图2 介质响应函数原理Fig.2 Principle of dielectric response function

极化系数是频率的复函数，其代表的不仅是极化组成的幅值，也表明了其相位角．其实部 χ’(ω)给出了极化的幅值，与激励电场相位一致，虚部 χ’(ω)给出了与电场正交的方向．考虑 Maxwell方程式定义的全电流包括直接电导电流及位移电流，即

利用 F [∂ D /∂t ] = jωD的傅里叶变换特性，对式(5)进行傅里叶变换得

式(1)中D(t)的傅里叶变换为

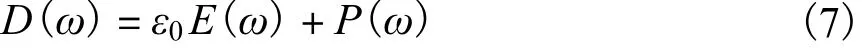
将式(3)、式(7)代入式(6)可得

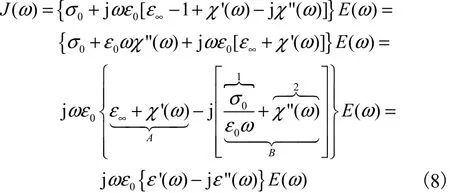
式中 A、B分别代表全电流的容性及阻性电流．阻性电流(B)与激励电场 E(ω)的相位一致，是介质的损耗引起．阻性电流B中的1项是由介质中自由电荷移动造成的欧姆损耗，而 2项为介质损耗，在激励电场下累积的束缚电荷的惯性造成[16-17]．可见，复极化常数的实部表示位移电流与激励电场垂直的部分，对其损耗无贡献，而其虚部给出了位移电流与激励电场同相位的部分，为损耗部分．因此，缓慢极化的过程可以通过测试正弦激励下的电流幅值和相位来研究．由于单一的频率可视为时间函数，因此电流可写为

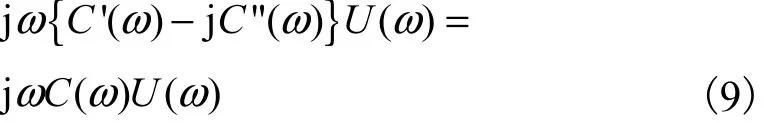
式中：σ0为介质的电导率；C(ω)是频率的函数，在不同频率或者特定频率范围内，老化、温度、微水含量将改变其值，频率响应法评估绝缘状态即检测老化对频率响应的影响．

2 实验测试

搭建如图3所示的实验平台，将绝缘纸板置于电极之间，并浸于变压器油中，利用烘箱来控制测试时温度．为了消除边缘效应，使得驱动电极与感应电极之间的电场电力线平行，在感应电极外围增加保护电极．

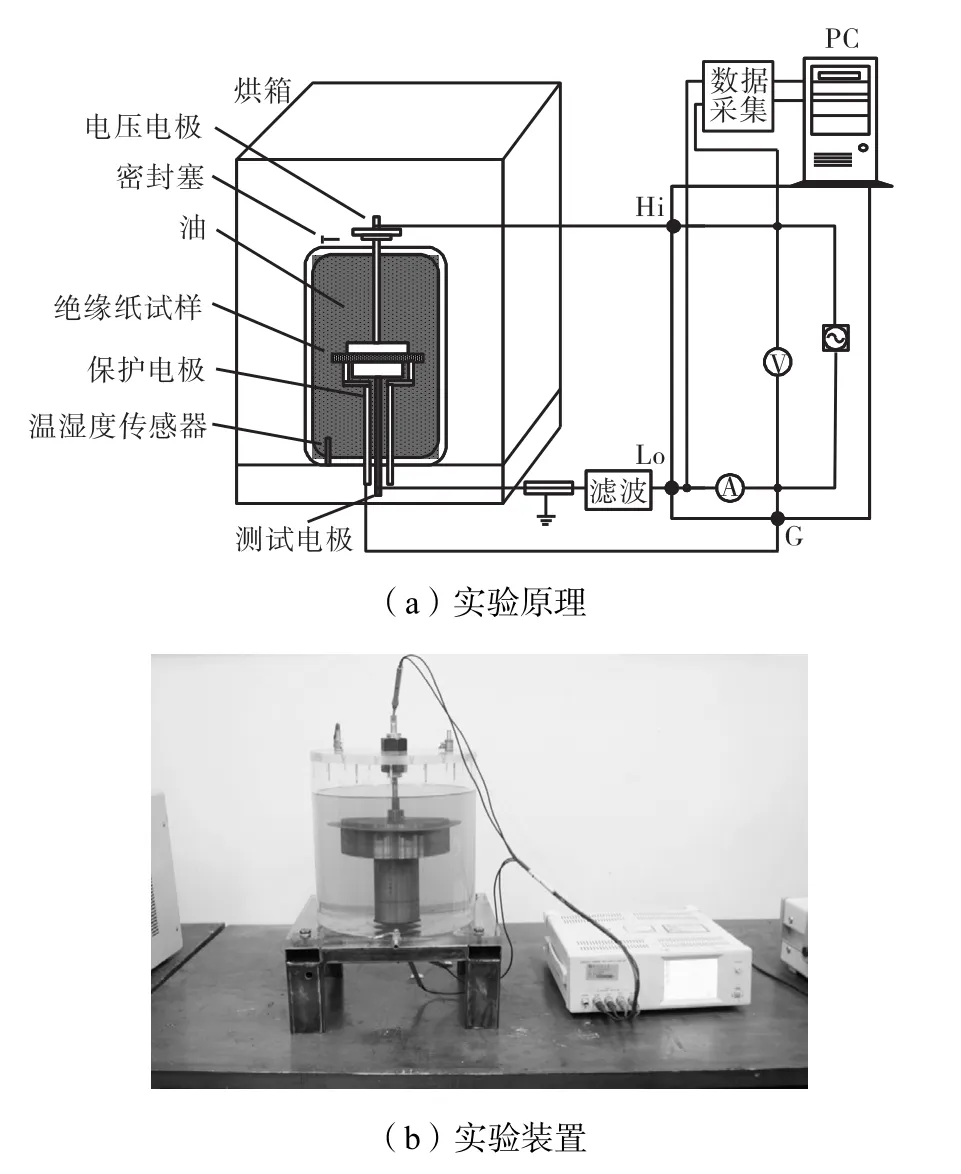
图3 实验系统装置Fig.3 Setup of experimental system

注油之前测试容器在真空中充分干燥，然后注入经过真空处理及干燥的工业级 25#纯净变压器油(微水含量低于 8×10-6)．绝缘纸(含 90%纤维素、6.2%的半纤维素、3.8%木质素)试样厚 1,mm，直径为100,mm，制成与极化电极一致的圆盘型．绝缘纸首先置于空气中吸收微水，利用高精度天平观察绝缘纸重量变化，初选出不同水分含量的试样，再利用 Karl Fisher 滴定法测试出准确的不同微水含量(0.5%、1.0%、2.0%、3.0%、4.0%，质量分数，下同)试样，将试样置于密封容器中2周，使得其微水分布均匀．

试样组 1，用于测试不同微水含量油纸复合绝缘频率响应，取水 0.5%、1.0%、2.0%、3.0%、4.0%微水试样浸于工业级 25#纯净变压器油中，密封后置于温度为 50,℃烘箱中 2周，使油纸复合绝缘微水扩散达到稳态；试样组 2，用于测试不同温度下油纸复合绝缘频率响应，将 2.0%微水含量绝缘纸，浸于纯净新变压器油中，密封后分别放置于设定温度为10,℃、30,℃、50,℃、70,℃的烘箱中 2周，使油纸复合绝缘微水扩散达到稳态．

3 测试结果及分析

3.1 不同微水含量油纸复合绝缘频率响应

在50,℃测试微水含量分别为0.5%、1.0%、2.0%、3.0%、4.0%的油纸绝缘频率响应，结果如图4所示．

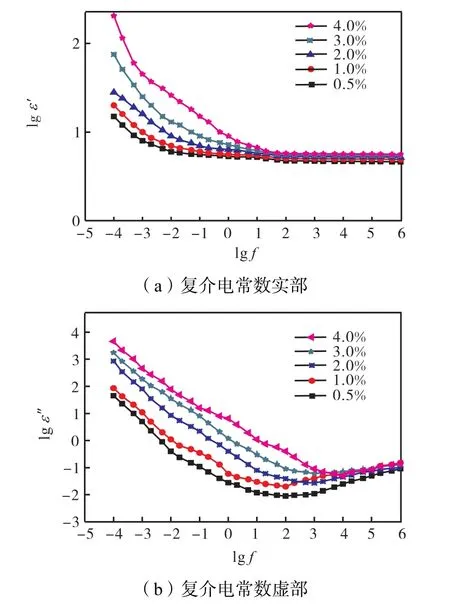
图4 50,,,℃时不同含水油纸复合绝缘频率响应Fig.4 Frequency dielectric response of oil-paper with different moisture contents at 50,,,℃

从图中可以看出，50,℃时，复介电常数实部ε′、虚部ε′随微水含量的增加而增大，尤其是在低频段，在高频段趋于一致．复介电常数与驱动频率、温度以及水分的关系，可以表示成半经验公式[18-19]为

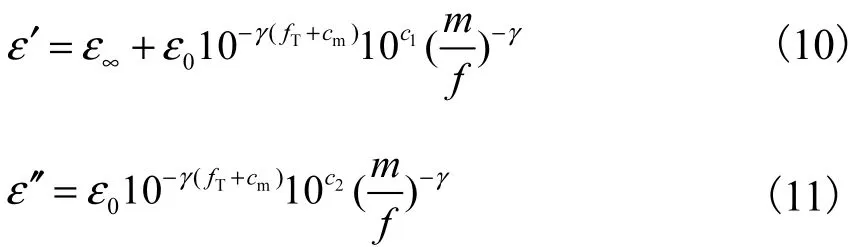
式中：γ、c1、c2为待定系数；fT为与温度相关的修正子函数．等效变换为

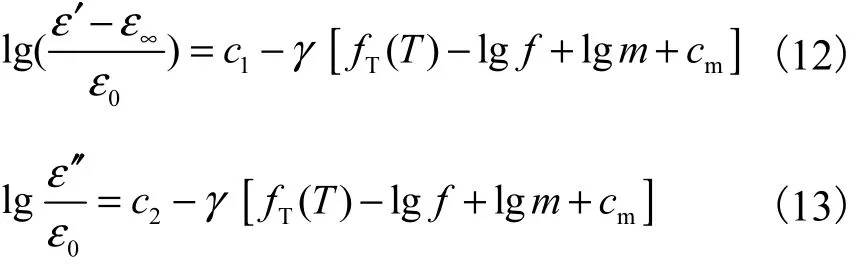
式中：γ (lg m＋cm)为微水含量的相关函数，γ (lg f)为频率函数，γ fT(T)为温度函数．由于图 4(a)给出的是ε′，做变换

取油纸绝缘 ε∞/ε0＝3，根据图 4，以微水含量为横坐标，可得lg[(εε∞′−)/0ε]，lg(0/εε′)与频率、微水含量的关系，如图5所示．

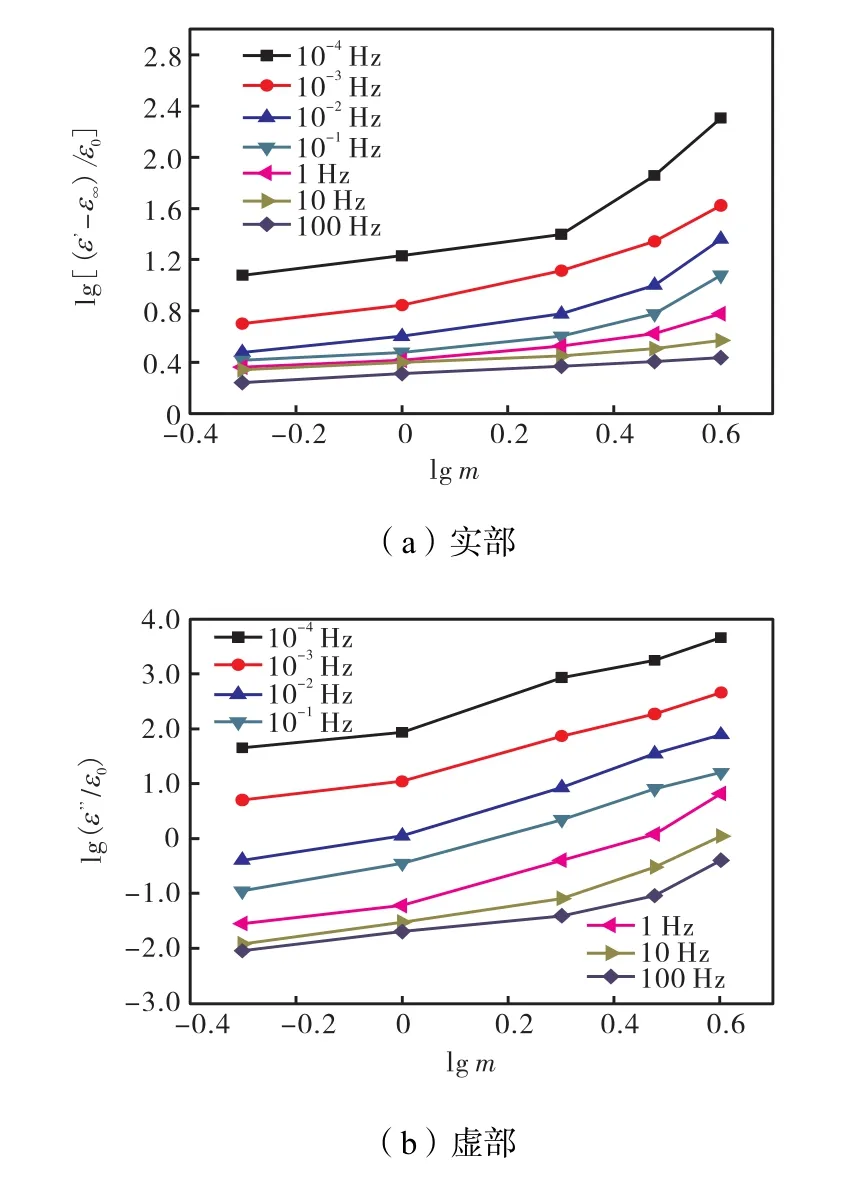
图5 50 ℃下不同微水含量、不同频率复介电常数Fig.5 Real part and imaginary part of different moisture content samples at different frequencies at 50 ℃

由图 5可以看出，在单个频率下，随着微水含量的增加，油纸绝缘复介电常数增大，其形状基本相同，且呈近似线性增加，特别是低微水含量区段．同时，在 100,,Hz以下，随着频率增加，油纸绝缘复介电常数减小．利用线性拟合的方法，求出 50,,℃温度的复介电常数实部和虚部的表达式为

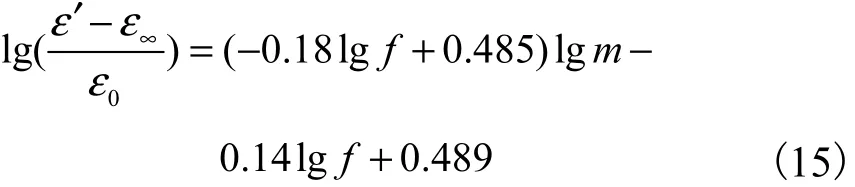
对照式(12)和式(13)，数据拟合结果与半经验公式形式类似．但 lg,m的待定系数在式(15)和式(16)中为频率的一个函数，形成一项频率与微水含量乘积式，这与拟合方法有一定关系．同时，从图 5可以看出，随着频率的增加，复介电常数对微水含量的斜率逐渐减小，反映出 lg,m、lg,f对复介电常数的共同影响机制．

针对式(15)和式(16)作复介电常数与微水含量与频率关系的拟合曲面，如图 6所示．拟合曲面能反映 50，℃下，油纸绝缘复介电常数与不同微水含量，不同频率的关联关系．

图6 50,℃下不同微水含量、不同频率复介电常数拟合曲面Fig.6 Modelled surface of complex dielectric permittivity with different frequencies and moisture contents at 50,℃

3.2 不同温度油纸复合绝缘频率响应

为研究温度对油纸复合绝缘频率响应的影响，在10,℃、30,℃、50,℃、70,℃时对比测试 2%微水含量油纸绝缘复介电常数频率响应，如图7所示．

随着温度增加，油纸复合绝缘复介电常数虚部值向高频率方向移动，其形状基本不变．根据 Arrhenius关系[17]有

式中：Ea为活化能；k为玻耳兹曼常数．

因此，lg,ε应与 1/T成线性比例．根据图 7，以温度为横坐标，可得lg[(εε∞′−)/ε0]，lg(0/εε′)与频率、温度的关系，如图8所示．

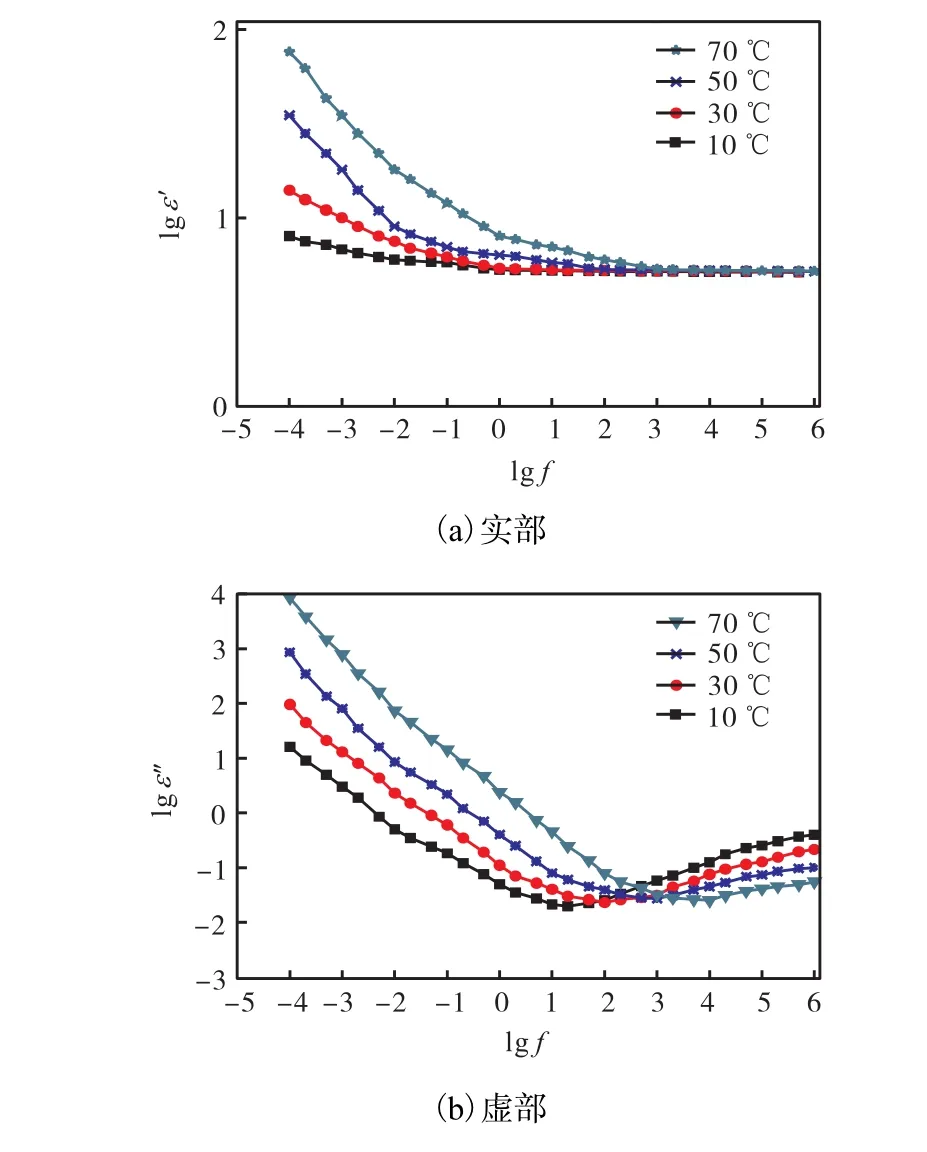
图7 不同温度下2%微水含量的油纸绝缘复介电常数Fig.7 Complex permittivity data of oil-paper with 2% moisture content at different temperatures

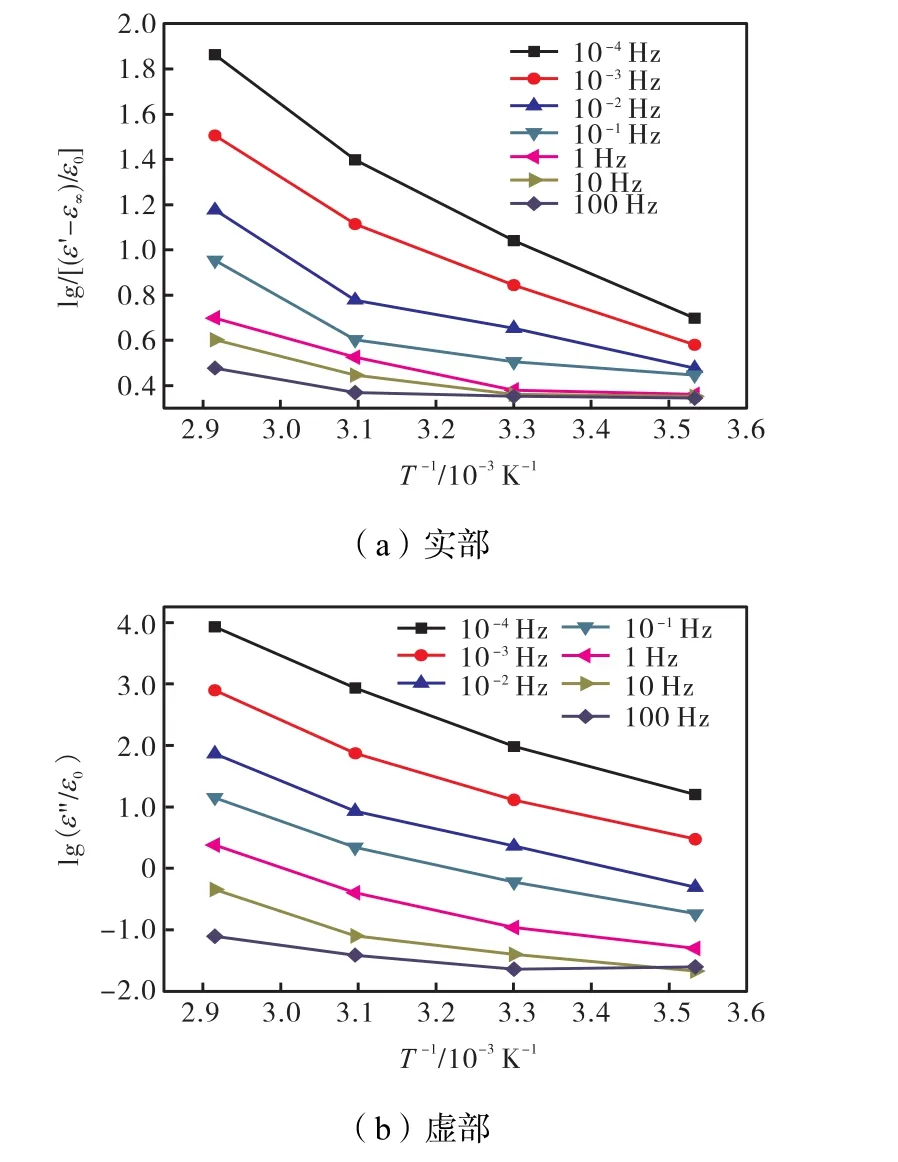
图8 不同温度、不同频率下2%微水含量的复介电常数Fig.8 Real part and imaginary part of oil-paper with 2%moisture content at different temperatures and frequencies

由图 8可以看出，在单个频率下，随着温度的增加，油纸绝缘复介电常数增大，其形状基本相同，且呈近似线性增加．同时，在100，Hz以下，随着频率增加，油纸绝缘复介电常数减小．利用线性拟合的方法，求出 2%微水含量下不同温度、不同频率复介电常数实部和虚部的表达式为

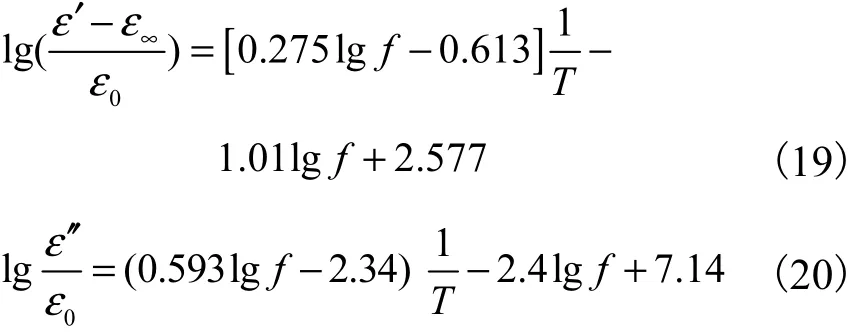
对照式(12)和式(13)，数据拟合结果与半经验公式形式类似．fT(T)对应于 1/T，fT(T)的待定系数在式(19)和式(20)中为频率的一个函数，形成一项频率与温度乘积式．针对式(19)、式(20)作复介电常数与温度与频率关系的拟合曲面，如图 9所示．拟合曲面能反映 2%微水含量油纸绝缘复介电常数与温度、频率的关联关系．

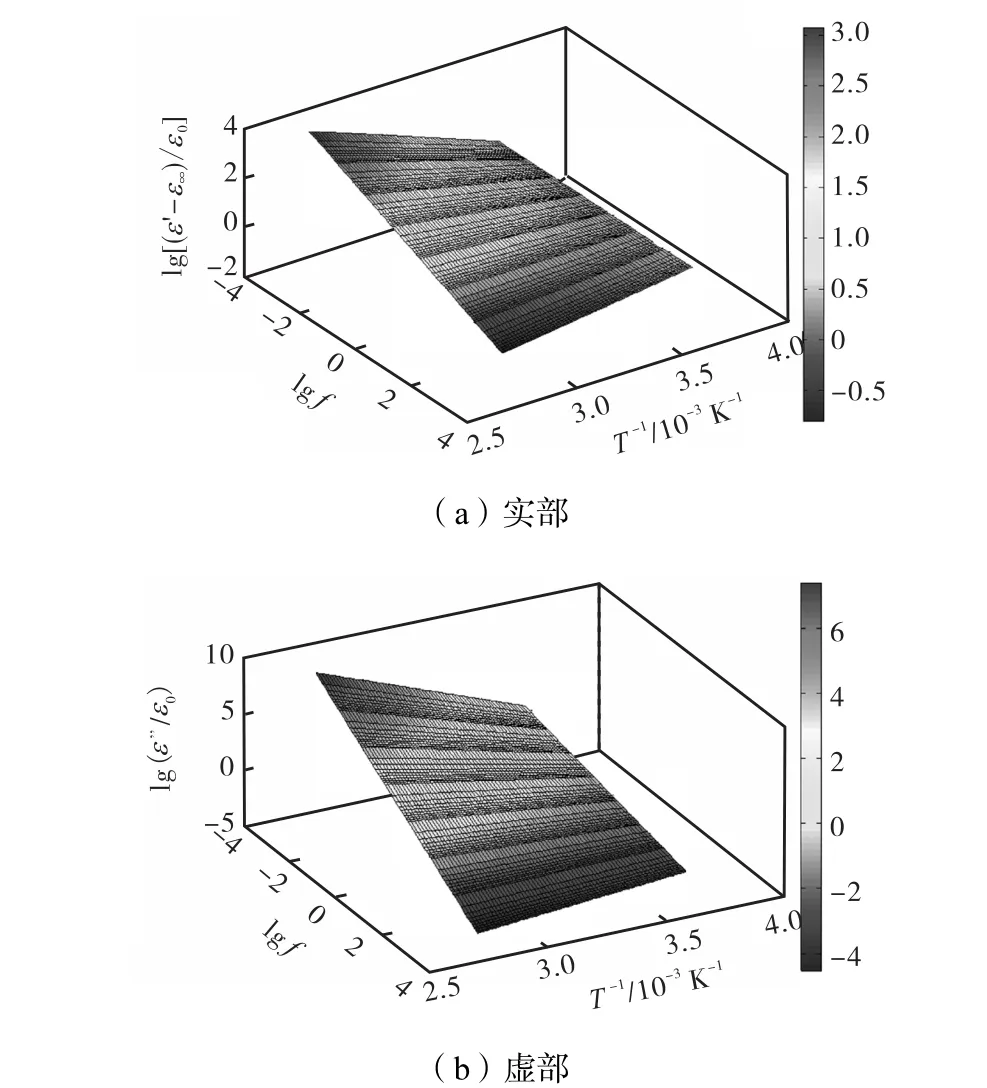
图 9 不同温度、不同频率下 2%微水含量的复介电常数的拟合曲面Fig.9 Modelled surface of complex dielectric permittivity with 2% moisture content at different temperatures and frequencies

由于温度及微水含量对复介电常数的影响相互独立[19]．根据叠加定理，结合式(15)、式(16)、式(19)和式(20)，可得到油纸绝缘复介电常数与温度、微水含量、频率的关系式为

式(21)和式(22)说明在温度和驱动频率一定时，测量油纸绝缘复介电常数的实部或虚部都能得出该试品中的微水质量分数．其实部变化说明微水相对介电常数对干燥绝缘纸板相对介电常数的影响．而虚部变化代表微水的微弱导电性产生的损耗．

3.3 实验验证

取 2%的微水含量纸绝缘在50,℃、0.001,Hz下测试的复介电常数，分别将微水含量及所处温度设为未知，以式(15)、式(16)、式(19)～式(22)计算其微水含量及所处温度，如表1所示，可以看出，相同温度下微水含量与复介电常数关系式(15)、式(16)能较为有效地评估油纸绝缘微水含量，但存在较大偏差，较油纸绝缘复介电常数与温度、微水含量、频率的关系式(21)、式(22)评估误差大；相同微水含量下温度与复介电常数关系式(19)、式(20)也能较准确评估该微水含量下油纸绝缘所处温度，但较式(21)、式(22)误差大．同时，实部的评估较虚部评估更为准确．

表1 实际温度及微水含量与计算值比较Tab.1 Comparison of measured and real moisture content and temperature

4 结 语

为研究变压器油纸复合绝缘中微水含量及温度对其绝缘性能的影响，对电介质响应法进行了分析建模，搭建了频率响应测试装置，测试了不同微水含量、不同温度条件下油纸复合绝缘 10-4～106，Hz范围内的频率响应．从图4(a)和图7(a)可以看出，随着温度升高、微水含量增加，油纸复合绝缘复介电常数的实部在 100,Hz以下相应增加，1,000,Hz以上基本不变并趋于一致．图 4(b)表明，不同微水含量下油纸复合绝缘复介电常数虚部形状基本保持不变，而随着微水含量的增加，其值增加．图 7(b)表明，随着温度增加，油纸复合绝缘复介电常数虚部值向高频率方向移动，其形状基本不变．通过最小二乘法拟合，分别得到了油纸绝缘复介电常数特定温度条件下与微水含量及频率的关联关系式，特定微水含量下与温度及其频率的关联关系式，并得到相应的拟合曲面，通过对比拟合曲面与实验测试值，表现出较好一致性．最后，通过叠加定理，得到了油纸绝缘复介电常数与微水含量、温度、频率的关联关系，使得微水及所处温度的评估更为准确．在计算过程中，忽略了变压器油中微水对绝缘纸中微水含量的影响，沿用浸油前绝缘纸中的微水含量，对系统的计算和评估造成了误差，同时，由于变压器油纸绝缘的复介电常数在高频阶段趋于一直，变化规律不明显，因此在评估的过程中主要是针对低频阶段，高频阶段的微小变化规律需要更细致的研究．文中所建立的油纸绝缘复介电常数与温度、频率、微水含量的关联关系，实现了在温度和驱动频率一定时，评估油纸绝缘微水含量．这就为应用频率响应法评估变压器油纸绝缘状态及其故障诊断奠定了基础．

［1］ Lundgaard L E，Hansen W，Linhjell D，et al.Aging of oil-impregnated paper in power transformers[J]. IEEE Transactions on Power Delivery[J]. 2004，19(1)：230-239.

［2］ Du Y，Zahn M，Lesieutre B C，et al. Moisture equilibrium in transformer paper-oil systems[J]. Electrical Insulation Magazine，1999，15(1)：11-20.

［3］ Saha T K，Yao Z T. Experience with return voltage measurements for assessing insulation conditions in service-aged transformers[J]. IEEE Transactions on Power Delivery，2003，18(1)：128-135.

［4］ Saha T K，Purkait P. Investigation of polarization and depolarization current measurements for the assessment of oil-paper insulation of aged transformers[J]. IEEE Transactions on Dielectrics and Electrical Insulation，2004，11(1)：144-154.

［5］ Linhjell D，Lundgaard L. Dielectric response of mineral oil impregnated cellulose and the impact of aging[J].IEEE Transactions on Dielectrics and Electrical Insulation，2007，14(1)：156-169.

［6］ Saha T K，Purkait P. Understanding the impacts of moisture and thermal ageing on transformer’s insulation by dielectric response and molecular weight measurements[J]. IEEE Transactions on Dielectrics and Electrical Insulation，2008，15(2)：568-581.

［7］ 刘 君，吴广宁，周利军，等. 变压器油纸绝缘频率响应特性影响因素[J]. 西南交通大学学报，2011，46(2):282-286.Liu Jun, Wu Guangning, Zhou Lijun, et al. Factors influencing dielectric frequency response of oil-paper insulation[J]. Journal of Southwest Jiaotong University,2011，46(2)：282-286(in Chinese).

［8］ Blennow J，Gubanski S M. Field experiences with measurements of dielectric response in frequency domain for power transformer diagnostics[J]. IEEE Transactions on Power Delivery，2006，21(2)：681-688.

［9］ Ekanayake C，Gubanski S M，Graczkowski A，et al.Frequency response of oil impregnated pressboard and paper samples for estimating moisture in transformer insulation[J]. IEEE Transactions on Power Delivery，2006，21(3)：1309-1317.

［10］ Ekanayake C. Diagnosis of Moisture in Transformer Insulation-Application of Frequency Domain Spectroscopy[D]. Goteborg：Department of Materials and Manufacturing Technology, Chalmers University of Technology，2006.

［11］ Gubanski S M，Boss P，Csépes G. Dielectric response methods for diagnostics of power transformers[J]. IEEE Electrical Insulation Magazine，2003，19(3)：12-18.

［12］ Du Y，Zahn M，Mamishev A V，et al. Moisture dynamics measurements of transformer board using a threewavelength dielectrometry sensor[C]//IEEE International Symposium on Electrical Insulation. Montreal，1996：53-56.

［13］ Garcia B，Burgos J C，Alonso A，et al. A moisture-inoil model for power transformer monitoring(Part Ⅱ)：Experimental verification[J]. IEEE Trans on Power Delivery，2005，20(2)：1423-1429.

［14］ 殷之文.电介质物理学[M]. 北京：科学出版社, 2003.Yin Zhiwen. Dielectric Physics[M]. Beijing：Science Press, 2003(in Chinese).

［15］ 赵孔双.介电谱方法及应用[M]. 北京：化学工业出版社，2008.Zhao Kongshuang. Dielectric Spectroscopy Method and Application[M]. Beijing：Chemical Industry Press，2008(in Chinese).

［16］ Zhou L J，Wu G N，Liu J，Modeling of transient moisture equilibrium in oil-paper insulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation，2008，15(3)：872-878.

［17］ Jonscher A K. Dielectric Relaxation in Solids [M]. London：Dielectrics Press Limited，1996.

［18］ 戴恒震. 变压器绝缘纸板微水分介电测量原理及其测量系统的研究[D]. 大连：大连理工大学机械工程学院，2004.Dai Hengzhen. Principle of Dielectrometry Measurements of Moisture Content in the Pressboard and Researeh on the Measurement System[D]. Dalian：School of Mechanical Engineering, Dalian University of Technology，2004(in Chinese).

［19］ Mamishev A V，Du Y，Lesieutre B C，et al. Evaluation of diffusion-driven material property porfiles using three wavelength interdigital sensor[J]. IEEE Transactions on Instruction and Measurement，2001，8(10)：785-798.