基于传感器网络的分布式生化气体源参数测定算法

张 勇 ，孟庆浩，吴玉秀，曾 明

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津商业大学信息工程学院，天津 300134)

随着传感器网络技术的不断发展，其在环境监测领域的应用也越来越广泛，其中对生化气体源参数测定问题[1-2]的研究在近些年受到越来越多的关注．生化气体源参数测定是指运用概率估计的方法确定监测环境中的生化气体源的位置、释放率、扩散系数等参数．该问题也被认为是对生化气体在环境中扩散建模问题的逆问题[1]．

文献[3]提出了一个完整的检测和估计理论框架并运用静态传感器阵列采集信号实现蒸汽源定位. 文献[4]对问题进行了扩展，采用一个移动传感器节点取代文献[3]中静态传感器阵列，实现了蒸汽源定位，同时对移动节点在信号采集过程中的最优路径规划问题展开研究．文献[5]把应用延伸到对地雷的监测中，对雷场中传感器节点的部署和成功检测到地雷的概率之间的关系进行研究．以上研究均基于相同的生化气体物理扩散模型且模型简单，参数测定只针对源位置坐标一个参数展开研究，采用的是极大似然估计算法．文献等[6]提出一种基于最小二乘算法的 2步气体源定位算法，该算法第1步先使用固定的传感器节点采集浓度信号，并在给定的气体扩散模型的基础上对气体源的位置进行预估运算，给出一些类似气体源坐标点的集合；第2步对这些不同传感器节点通过预估运算得到的气体源坐标点集合求交集，其交集可以用来最后判定是否为气味源．在该算法中运用了气体释放率来对预估气体源的位置坐标进行确认．文献[7]对一个放射源进行参数测定工作，主要包括源的位置预估和释放率的估计．

以上的生化气体源参数测定算法均是通过传感器网络完成信号采集并将采集的信号发送到数据融合中心，生化气体源的参数估计在数据融合中心实现．当传感器节点数目不太多时，这种方法实现简单，随着传感器节点数目的增加，其运算量和通信负担将急剧增大，采用此方法将严重影响系统的性能．

笔者基于分布式卡尔曼滤波(distributed Kalman filter，DKF)算法[8]，提出了分布式扩展卡尔曼滤波(extended Kalman filter，EKF)和无迹卡尔曼滤波(unscented Kalman filter，UKF)迭代估计算法用于气体源的位置和释放率的估计，并通过计算机仿真对这2种方法进行了分析比较．

1 问题描述

生化气体源的气体扩散过程可以描述为一个概率的随机过程，因此，采用概率估计的方法对气体源参数进行测定应是一种可行的解决方法．如图 1所示，假设在二维区域中存在 1个气体源，坐标用(xs, ys)表示，同时在该环境区域内随机部署 m个传感器节点，各个节点的坐标已知或者可以通过节点自身定位算法获得，用(xi, yi)表示第 i个节点的坐标，i = 1 ,2,… ,m ．在实际应用中，每个节点配置一个可采集气体或气味浓度信息的传感器．假定 zk= { zk:k=1,2,…,N}为位于(xi, yi)节点在不同时间周期内所采集到的浓度测量值．则气体源测定问题可以描述为运用不同的浓度测量值对气体源参数向量= [,,ˆ]T进行估计的过程．其中，ˆ为气体释放率估计值，[,]为气体源坐标估计值．

图1 生化气体源参数测定问题描述Fig.1 Geometry of chemical odor source determination problem

1.1 气体分布模型

运用概率估计的方法解决生化气体源的参数测定问题需要给定气体分布的物理模型．准确地建立实际监测环境下的气体分布模型是非常困难的，而且对于突发气体泄漏事件来说也是不现实的，因为气体的扩散通常受到湍动气流影响，其随机性很大．但是，通过湍流扩散理论可以推导相对简单的用于描述时均气体分布的模型．笔者采用文献[9]中提出的时均气体分布模型．此种模型可以描述在时均风速恒定且均匀(homogeneous)、各向同性(isotropic)的湍动气流作用下的气体分布状况．假设生化气体点源位于地平面上 ( xs,ys)处，则气体分布模型表达式为

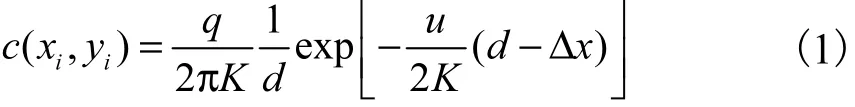
式中：c(xi, yi) 为监测区域中传感器节点(xi, yi)处的浓度值；q为气体释放率；K是湍流扩散系数；u为风速；d是区域中传感器节点(xi, yi) 到气体源 ( xs,ys)的距离

如果假设风向沿着x轴，则式(1)可以简化为

根据上述的模型可以得出在一定区域内气体浓度分布．

1.2 测量模型

系统的测量模型，即传感器节点(xi, yi)的浓度测量值 zk可以描述为

式中：x =[xs, ys,q]T；非线性函数 hk(x)为位置(xi, yi)处观测到的气体理想浓度值；vk为环境噪声．

2 分布式气体源参数测定算法

根据贝叶斯滤波理论[10]，所有关于状态变量的信息都可以从其概率密度分布获得．从统计方法的角度，生化气体源参数测定可以看作在给定浓度观测值的情况下，求解包含气体源状态参数信息的后验概率密度p ( x z1,z2,… ,zk)的状态估计问题．

当状态空间模型是线性高斯模型，同时状态噪声和观测噪声都是加性高斯噪声，通常可以采用卡尔曼滤波(Kalman filter，KF)预估状态．而环境中生化气体的扩散过程是一种非线性随机过程，因此采用针对非线性系统的EKF[11]和UKF[12]来完成气体源参数向量x的估计．

EKF和UKF都把后验概率近似描述为一种符合N(xk; xkk, Pkk)的高斯分布，其中 xk为k时刻的状态参量，xkk和Pkk分别为均值和方差，其值可以通过迭代的方法得到．

2.1 EKF算法

针对非线性模型，利用泰勒展开来线性化状态方程和观测方程，用高斯分布来近似状态的后验分布，然后使用KF进行估计．EKF算法表示为

式(8)和式(9)分别是 k-1时刻的状态均值和状态方差预测方程．下标kk−1含义为在 k −1时刻的测量值基础上对k时刻状态的估计，kk含义为得到 k时刻测量值后对状态进行更新的过程．

式中：Sk为估计值与真值残差方差，Rk；Kk为Kalman滤波增益，Kk=Pkk−1；Rk为测量噪声的方差；和分别为非线性函数fk−1(x)和 hk(x)局部线性化值．

式(10)和式(11)表述的是得到k时刻测量值 zk后系统的状态均值和状态方差的更新过程．

由于是对释放率恒定的静态气体源进行位置和释放率估计，因此，气体源的位置和释放率是不变的，即向量x是恒定的．转换方程可以简化为

2.2 UKF算法

与EKF方法用泰勒级数近似非线性转换函数不同，UKF用一组采样点表示系统状态的概率分布函数．确切地说，UKF利用这组采样点通过无迹变换近似得到后验概率分布．无迹变换是 UKF算法的核心和基础[10]，UKF利用无迹变换代替泰勒级数展开，递推估计高斯随机变量的均值和方差．假设系统采样点的权重系数为，i = 1 ,2,… ,M ．权重系数可以通过无迹变换进行更新．状态预估均值和状态预估方差的计算式为

测量值的预估方程为

得到 k时刻测量值kz后系统的状态均值和状态方差的更新过程为

矩阵 Pxz和 Pzz的计算式分别为

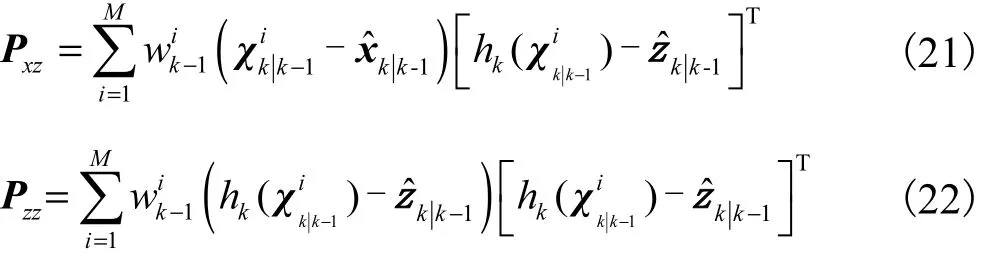
2.3 分布式迭代估计算法

分布式迭代估计算法由算法初始化、迭代运算和算法结束判定3个部分构成．算法流程如图2所示．

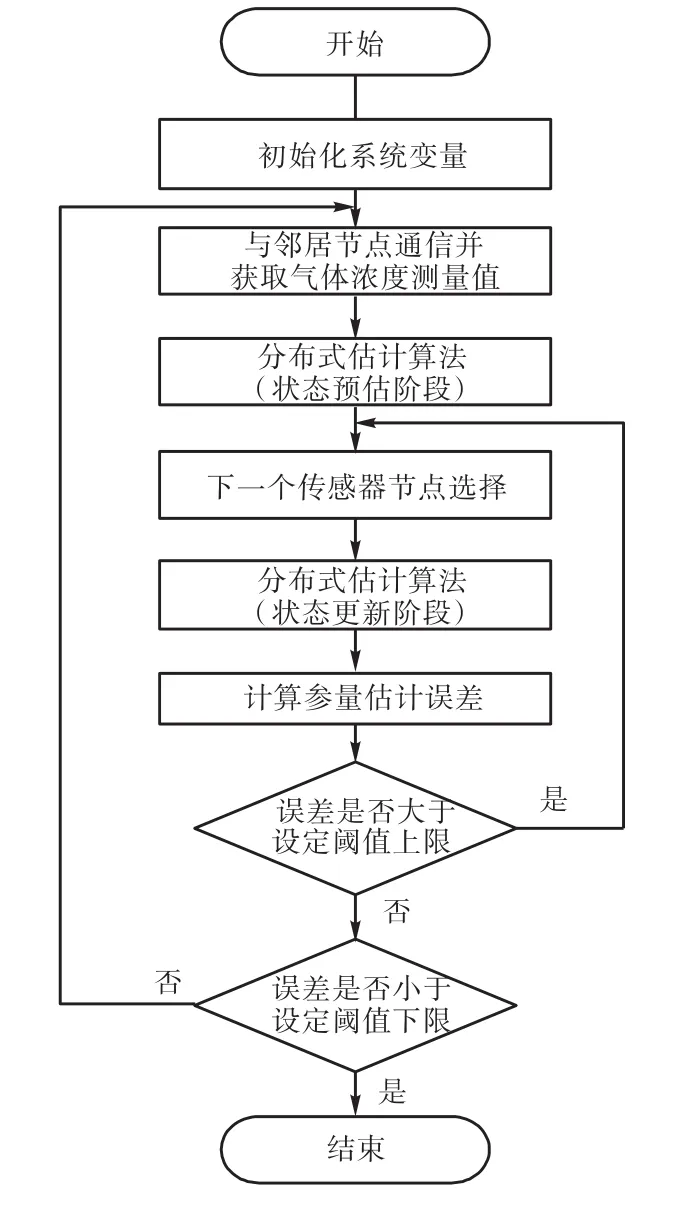
图2 分布式估计算法流程Fig.2 Flow chart of distributed estimation algorithm

在算法初始化阶段，需要选定一个节点作为初始节点．初始节点可以是部署在环境中的任意节点，但若初始节点离气体源较近，则估计过程相对容易，因此为了验证本文分布式迭代估计算法的可行性，初始节点均在距离气味源较远的节点集合中选择．初始节点确定以后，该节点在一个采样周期内对所处的环境进行浓度信息采集．同时在采样过程中该节点需要和邻居节点完成信息共享以获得尽可能多的测量值．初始节点发布广播信息给单跳路由的邻居节点，接收到广播信息的邻居节点返回其对应的坐标信息和相应浓度测量值，根据这些信息由初始节点完成对目标参数的预估运算，并给出估计结果．初始节点得到的估计结果需要传递到邻居节点中的某个传感节点，然后进一步完成迭代运算，其目标是不断地向接近气味源的节点传递气体源参数预估信息．

下一个节点的选择通常是由节点坐标与气体源坐标估计值距离函数来判定，ˆd值最小的某个邻居节点通常被选为下一个路由节点．该节点再通过自身及其邻居节点提供的测量值对接收到的参数预估信息进行更新，然后以此类推完成迭代运算．

这种迭代估计算法所进行的“预估-更新”过程实际上是一种卡尔曼滤波的实现过程，算法的最终目的是通过尽可能少的路由节点把初始节点的信息传递到气味源附近的某个节点，并完成气体源的定位和释放率估计．由于不需要把测量信息传递到融合中心，且融合计算不集中在融合中心实现，而是分布到整个监测环境中的某些节点上实现，降低了系统的运算和通信消耗．

3 仿真结果与分析

为了验证算法的可行性，在 MATLAB平台上进行了仿真实验．仿真所用的计算机 CPU主频为2.4,GHz，内存为 2,GB．实验区域为 500,m×400,m的一个二维空间，如图3所示．

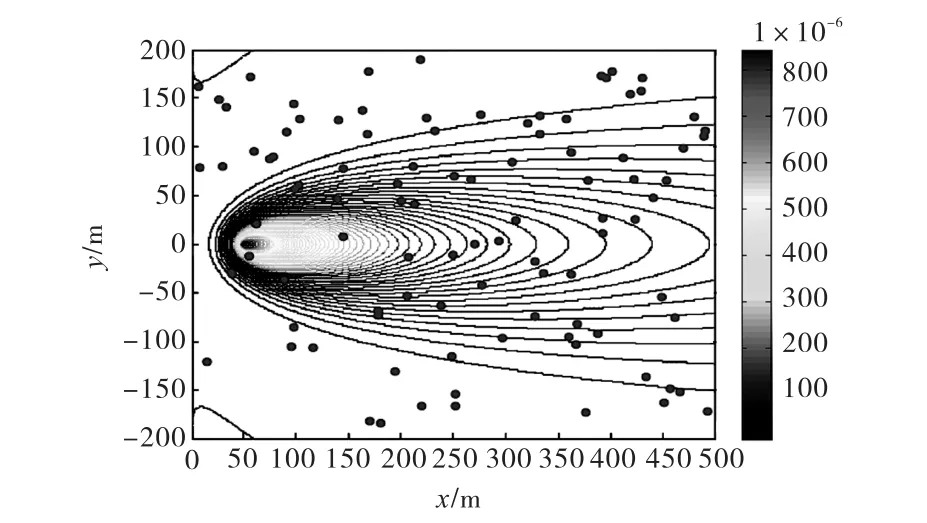
图3 气体源和100个传感器节点分布Fig.3 Deployment of chemical odor source and 100 random sensor nodes

假设气味源真实坐标为(50，0)，通过文献[9]中的气体扩散模型生成相应的浓度数据，其分布由等高线给出，其中释放率q选择为 30,mL/min，湍流扩散系数K为 30,cm2/s．100个传感器节点(用黑色圆点表示)随机的部署在监测环境区域内，假设每个节点的位置信息已知，在仿真实验中各个节点均可以实时采集并具有时空一致性．考虑到通常所用的金属氧化物半导体气体传感器的相对较长的响应和恢复，仿真中节点的浓度采样周期设为 5,s．对每个传感器节点而言系统模型噪声采用高斯白噪声(均值μ=0，方差 σi=3×10-6)．

对基于 EKF和 UKF的分布式迭代估计算法分别进行了研究和实现，并通过多次仿真实验对其性能进行了分析和比较．首先对2种算法在10种不同节点部署条件下的成功率以及成功实现的算法中参数估计误差均值进行了比较，然后在相同实验环境和条件下对 2种算法的估计结果与所需传感器节点数量之间的关系进行了分析．

在每一种节点部署条件下，分别选择 10个与气体源距离大于 400,m的不同传感器节点作为初始节点．每个初始节点运用EKF和UKF 2种不同的算法分别完成 10次迭代估计运算，记录 2种算法能够成功得到估计结果的次数，然后更换节点部署方案重复上面的运算．

算法完成运算的执行时间小于5,min则视为1次成功的迭代估计，否则视为 1次失败的运算(即没有收敛)．成功率定义为成功的次数除以总的实验次数(每种算法的总实验次数为1,000次)．最后在成功的迭代运算中，求估计误差Δx的算术平均值．

图4给出了不同节点部署条件下UKF算法和EKF算法的气体源定位误差均值、释放率估计误差均值和成功率3种统计结果．从图中可以看出：UKF算法的成功率高于EKF算法，表明UKF估计算法的收敛性能好于EKF算法；UKF算法估计误差均值比EKF小，说明UKF算法比EKF算法具有更高的估计精度．

图4 不同节点部署条件下成功的迭代算法统计结果Fig.4 Results of successful iterative algorithm with different sensor deployment

图 5给出了 2种估计算法时其中一次成功估计的过程．图中，黑色圆点代表参与了数据融合运算的节点；以黑色节点为圆心的黑色圆圈表示节点测量的浓度值大小，圆圈半径越大，表示浓度越高．为便于性能分析和比较，EKF算法和UKF算法都选择灰色节点(坐标为(475，112))作为其初始节点．EKF和UKF算法最终估计的气体源位置分别为(73，－47)和(55，11)．

图 5(a)中的星号和图 5(b)中的三角形符号分别表示EKF和UKF算法最终估计的气体源位置．由图中结果可以判定 UKF算法在定位过程中比 EKF算法使用的节点数目少，且路由路径短．这也表明UKF在运算过程中的计算量较小，从而定位速度比较快，同时通信消耗也会相应地低．

为了更清晰地看出 EKF和 UKF算法的估计精度与所使用传感器节点数量之间的关系，基于图5所示传感器节点分布及气味源位置，图6和图7分别给出了气体源位置和释放率估计误差随传感器节点数量的变化情况．从图6和图7中可以看出UKF算法定位精度和释放率估计精度均好于 EKF算法．对于UKF算法，收敛比较快，经过大约 20个节点后估计结果基本不再发生大的变化，而对于EKF算法，收敛过程相对缓慢，使用的节点也比较多，而且随着节点的增加其最终定位误差也比较大．

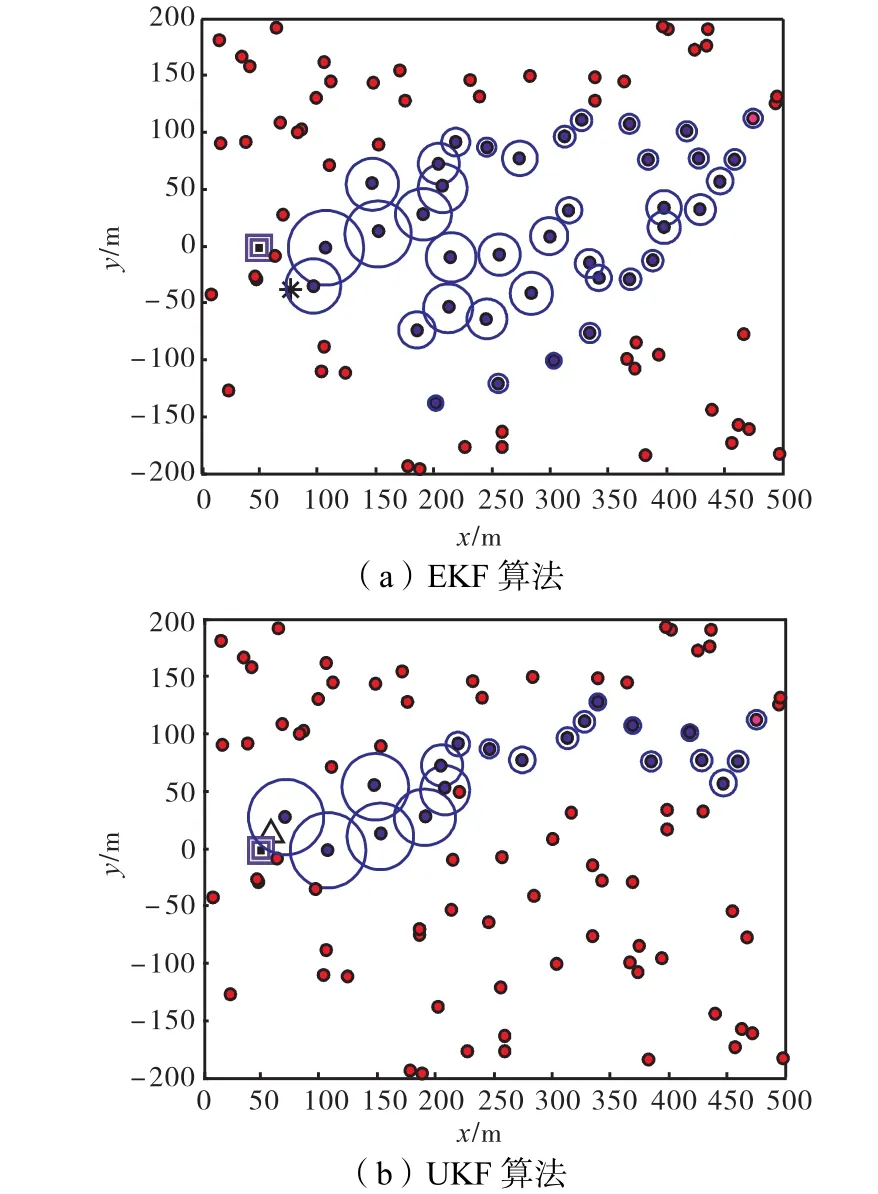
图5 2种不同算法分布式估计算法估计实例Fig.5 Example of two different distributed estimation algorithms

图6 气体源位置估计误差与传感器节点数量关系Fig.6 Position estimation error of chemical odor source with different sensor node numbers

图7 气体源释放率估计误差与传感器节点数量关系Fig.7 Emission rate estimation errors of chemical odor source with different sensor node numbers

4 结 语

研究了基于传感器网络技术实现生化气体源参数测定问题．针对传统的集中式算法中存在的问题提出了一种基于贝叶斯框架的分布式迭代估计算法，并分别运用分布式扩展卡尔曼滤波和无迹卡尔曼滤波方法进行了实现．初步的仿真实验表明：分布式卡尔曼滤波算法可用于生化气体源参数测定；无迹卡尔曼滤波算法在生化气体源参数估计的成功率和估计误差均值2个方面均好于扩展卡尔曼滤波算法；在相同的仿真条件下，无迹卡尔曼滤波算法比扩展卡尔曼滤波算法能够更快地收敛，即使用的传感器节点数目更少．

［1］ Keats W A，Yee E，Lien F S. Bayesian inference for source determination with applications to a complex urban environment[J]. Atmospheric Environment，2007，41(1)：465-479.

［2］ Oispuu M，Nickel U. Direct detection and position determination of multiple sources with intermittent emission[J]. Signal Processing，2010，90(5)：3056-3064.

［3］ Nehorai A，Porat B，Paldi E. Detection and localization of vapor-emitting sources[J]. IEEE Transactions on Signal Processing，1995，43(1)：234-253.

［4］ Porat B，Nehorai A. Localizing vapor-emitting sources by moving sensors[J]. IEEE Transactions on Signal Processing，1996，44(4)：1018-1021.

［5］ Jeremic J，Nehorai A. Landmine detection and localization using chemical sensor array processing[J]. IEEE Transactions on Signal Processing，2000，48(5)：386-395.

［6］ Matthes J，Groll L，Keller H B. Source localization by spatially distributed electronic noses for advection and diffusion[J]. IEEE Transactions on Signal Processing，2005，53(5)：1711-1719.

［7］ Pudykiewicz J A. Application of adjoint tracer transport equations for evaluating source parameters[J]. Atmospheric Environment，1998，32(9)：3039-3050.

［8］ Spanos D P，Olfati-Saber R，Murray R M. Approximate distributed Kalman filtering in sensor networks with quantifiable performance[C]//Proceedings of the 4,th international Symposium on Information Processing in Sensor Networks. Piscataway，USA，2005：133-139.

［9］ Ishida H，Nakamoto T，Moriizumi T. Remote sensing of gas/odor source location and concentration distribution using mobile system[J]. Sensors and Actuators B：Chemical，1998，49(6)：52-57

［10］ 匡兴红. 无线传感器网络中定位跟踪技术的研究[D].上海：上海交通大学电子信息与电气工程学院，2008.Kuang Xinghong. Research on Localization and Target Tracking in Wireless Sensor Networks[D]. Shanghai：School of Electronic Information and Electrical Engineering，Shanghai Jiao Tong University，2008(in Chinese).

［11］ Bar-Shalom Y，Li X R，Kirubarajan T. Estimation with Applications to Tracking and Navigation[M]. USA：John Wiley and Sons，2001.

［12］ Julier S，Uhlmann J，Durrant-White H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control，2000，45(3)：477-482.