Ghostburster模型鞍结分岔点附近放电模式的转迁控制

陈颖源，王 江，曾启明，陈伟乐，魏熙乐，邓 斌

(1. 天津大学电气与自动化工程学院，天津 300072；2. 香港理工大学机电工程学院，香港 999077)

在神经系统中，神经元的放电模式蕴含着大量的信息．声、光、电以及机械等外界刺激通过影响神经元的生理参数引发不同的放电模式，如峰放电、簇放电等．峰放电在动力学上对应着稳定的极限环[1-2]，而簇放电的动力学特性更加复杂[2-9]．受快慢离子通道的调节，神经元可表现出混沌簇放电[2-4]、反弹簇放电[5-6]等多种簇放电形式．研究认为簇放电在从受体神经元到脑皮层的神经信息处理中发挥了重要的作用[7-8]，而且还可以加强脑皮层各区域之间的联系[9]．同时，不正常的簇放电则会破坏神经系统的信息传递．比如帕金森患者发病时在丘脑中继细胞上观察到的大量的反弹簇放电[5-6]．

神经元随着参数的变化会产生分岔，从而引起不同放电模式的转换．所以，通过调整分岔点的位置，可以使神经元在某些参数下达到期望的放电特性[1,10]．文献[11]利用卡尔曼滤波器控制小脑皮层模型的频率和放电模式．文献[12]利用状态反馈控制来抑制心脏中不正常的动作电位．文献[13]利用washout滤波器控制Hopf分岔点来实现HH模型静息状态和周期放电状态之间的转换．washout滤波器不改变原系统的平衡点，其在神经系统 Hopf分岔控制[13-16]和混沌控制[16-17]中应用较广．但是，对神经系统进行鞍结分岔控制的研究鲜见文献报道．笔者从Ghostburster模型[18-19]极限环上的鞍结分岔点出发，通过washout滤波器调整鞍结分岔点的位置，以实现鞍结分岔点两端放电模式的转迁．

Ghostburster模型是来自于弱电鱼电敏感侧线叶(electrosensory lateral line lobe，ELL)椎体细胞的二室模型，有丰富的放电模式[18-19]．2000年，Lemon和Turner[20]分析了 ELL椎体细胞中频率的簇放电机制．2002年，Doiron等[18-19]研究了 ELL椎体细胞在外电场作用下的非线性特性，把多室结构降维为二室并命名为 ghostburster模型．他们提出该模型的簇放电是由快子系统固定点诡异(ghost)的鞍结分岔产生的，这种鞍结分岔有别于传统簇放电发生时快子系统从静息态到极限环的分岔类型[1]，静息态并不存在，簇放电的时间间隔主要由无限周期分岔决定，这种分岔形式称为“ghost”．这种特殊的簇放电为了解放电模式提供了新的见解．

笔者在 washout滤波器产生的控制效应的基础上，通过快慢系统分解，分析了 washout滤波器作用到鞍结分岔点上的内在机制，发现快子系统固定点的鞍结分岔和快子系统从周期一极限环转换到周期二极限环的临界点之间的相互作用是该模型周期放电和簇放电产生的关键因素．

1 Ghostburster模型的动力学分析

Ghostburster模型[18-19]是弱电鱼 ELL椎体细胞的二室模型．它描述了胞体和树突之间信息的传导，从整体上刻画了柱状细胞的动力学行为．Ghostburster模型包含了6个非线性微分方程．

1)胞体部分

2)树突部分

其中，式(1)和(3)分别为胞体和树突膜电压的微分方程，Iu为控制电流项．胞体和树突之间通过简单的耗散电流耦合．各个离子通道电流(INa,s，IDr,s，INa,d，IDr,d)受最大电导 gmax(单位为 m s/cm2)，S型激活和失活概率曲线w = n ,h,p)及通道时间常数τ(单位为ms)影响，其参数选择参见文献[18]．其他参数选择如下：gc=1，κ= 0 .4，VNa= 4 0mV，VK=−8 8.5mV ，Vleak=−7 0mV，gleak= 0 .18，Cm= 1 µF/cm2．本文用去极化电流 Is作为分岔参数来研究 Ghostburster模型的动力学特性．图1是放电频率f( f = 1 /TISI，ISI为峰峰间期)和最大Lyapunov指数λ随着分岔参数 Is变化的图形．

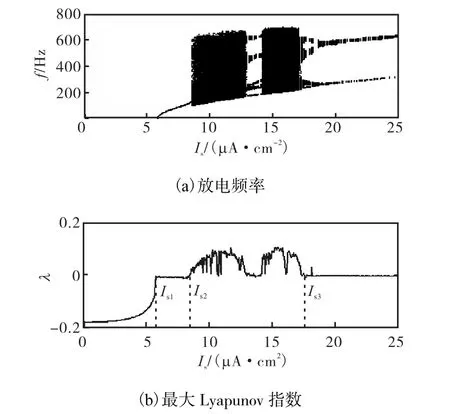
图1 放电频率f和Lyapunov指数λ随去极化电流Is变化的分岔图Fig1 Bifurcatim diagram of f and λ as Is varied

(1) 当Is＜Is1时，神经元处于静息状态，系统存在一个稳定的平衡点和一个不稳定的平衡点，这时f=0，λ=0．

(2) 当Is= Is1( ≈ 5 .8μ A /cm2)时产生了不变环上固定点的鞍结分岔，2个平衡点碰撞消失，产生一对稳定的极限环和不稳定的极限环．

(3) 当 Is1＜Is＜Is2时，稳定的极限环和不稳定的极限环共存．神经元呈现周期放电状态，这时峰峰间期(ISI)为常数，f也为常数，λ=0．在该区间内的典型响应如图2(a)和(b)所示．

(4) 当Is= Is2( ≈ 8 .5μ A /cm2)时产生极限环的鞍结分岔，这是一种接近余维2(near codimension-2)的鞍结分岔[1]．稳定的极限环和不稳定的极限环碰撞消失，从而产生混沌现象．

(5) 当 Is2＜ Is＜ Is3时，神经元不存在稳定的极限环．在大部分参数下其 ISI是变化的，故f也是变化的．λ＞0表明神经元处于混沌状态，而λ=0表明系统进入了周期窗口(比如 Is在 [ 13.13μA/cm2，13.73μA /cm2]区间内存在一个六周期解)．在该区间内的典型响应如图2(c)和(d)所示．

(6) 当 Is= Is3≈ 1 7.65μA /cm2时，系统在该参数附近产生倍周期分岔，产生了二周期解．

(7) Is＞Is3时神经元呈二周期簇放电状态，所以λ= 0 ．在该区间内的典型响应如图2(e)和(f)所示．

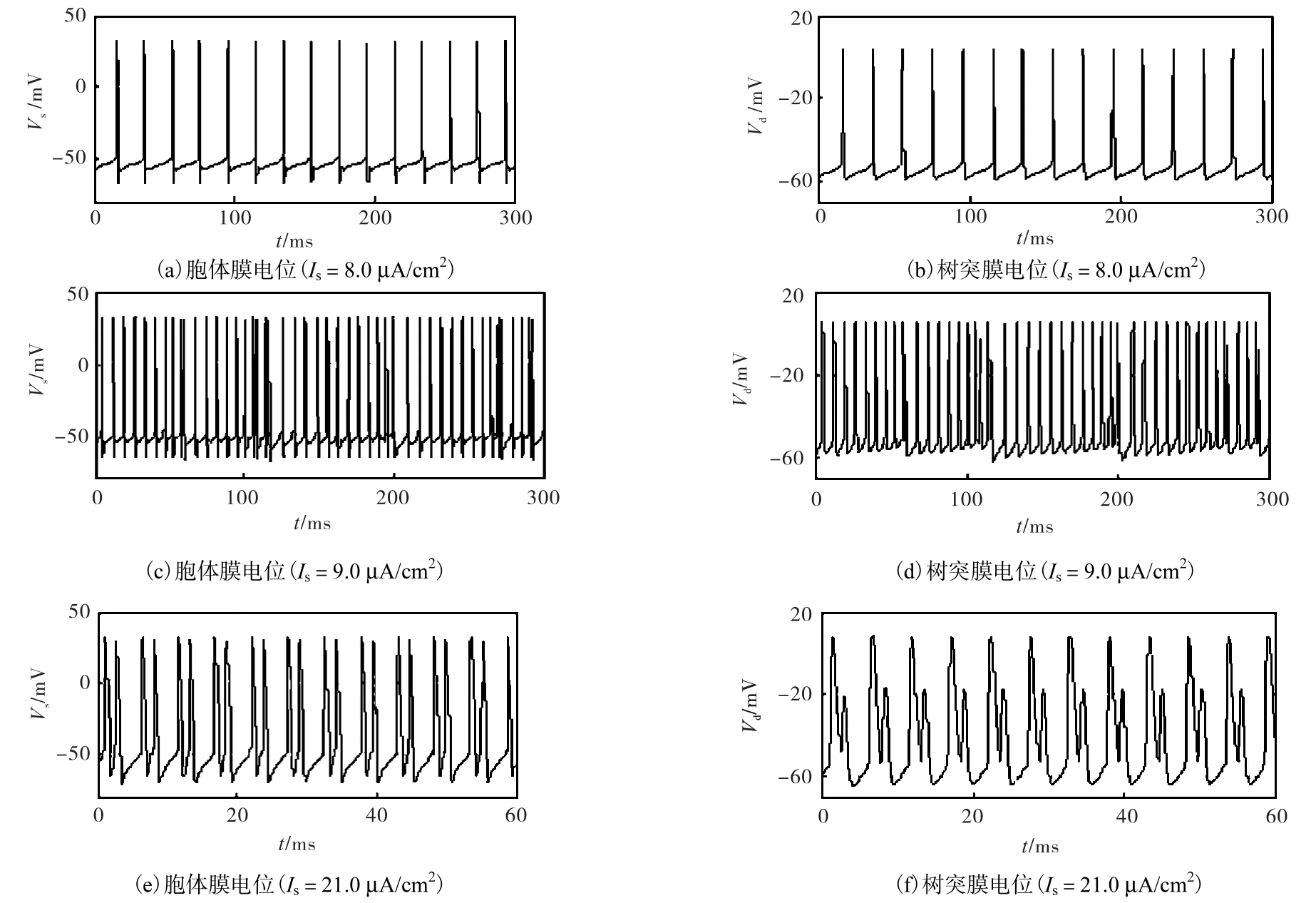
图2 Ghostburster模型在3类典型电流输入下的响应Fig.2 Time series of somatic membrane potential Vs and dendritic membrane potential Vd of ghostburster model with 3 different current stimulations

2 Ghostburster模型的 washout滤波器反馈控制

2.1 Washout滤波器

Washout滤波器实际上是一个高通滤波器，其稳态输入被滤除，而暂态输入则得到保留．一维washout滤波器[13,17,21]可设计为

式中：x为 washout滤波器的输入；d为 washout滤波器时间常数的倒数；z为 washout滤波器的状态；y为输出函数． ()gy是待设计的控制函数．滤波器有2个条件需要满足，一个是 d ＞ 0 以保证滤波器的稳定性．另一个是 g ( 0)= 0 以保留初始平衡点．加入washout滤波器后，新系统(式(1)～式(7))将变成七阶系统．因为 Vs在反馈系统中易于测量，令 x = Vs作为唯一的控制器输入．为了简化控制参数的选择，控制函数只包含一个线性项，表示为

式中K为反馈控制器增益．由图 1可知 Is=Is2(≈8.5μA/cm2)2端存在着2种不同的状态：周期放电和混沌簇放电．故本文把控制目标设定为实现这2种状态之间的相互转换．根据 Izhikevich的描述，Is2附近发生的是极限环上接近余维 2的鞍结分岔[1]，要从数值上精确确定分岔点的位置非常困难．所以，只能从经验上通过调节参数K和d来达到期望的特性．

2.2 Washout滤波器控制结果

2.2.1 从混沌簇放电到周期放电的转迁

图3为washout滤波器参数的变化对最大Lyapunov指数λ的影响．由图 3可知在同一d下随着K增加λ呈递减趋势，但是并不单调．而且，d不同时λ作为K的函数变化并无太大区别．K增加到一定值后λ为负值，说明神经元呈现周期放电状态．为了分析方便，把滤波器参数设置为 K = 0 .3、d = 0 .4.图 4表示的是加上控制器前后胞体和树突膜电压的时间序列．控制量在 t = 2 00ms 时加入．在经过一个短的暂态过程后，神经元从混沌簇放电转换为周期放电．图 5是加入控制器以后，λ和f随着 Is变化．因为washout滤波器并不改变平衡点的特性，第1分岔点仍然在 Is1= 5 .8μA /cm2处．第 2分岔点 Is2从8.5μA/cm2移至11.7μA/cm2，使I=9.0在区间s[Is1, Is2]内，模型呈周期放电状态．第 3分岔点 Is3从17.65μA/cm2延后至20.8μA/cm2．混沌区域[I ,I ]的s2s3大小几乎保持不变，只是做了一段平移．这是因为washout滤波器只是改变了全系统的极限环的鞍结分岔位置，而快子系统固定点的鞍结分岔几乎没有任何改变造成的．

图3 在不同d下λ随K变化的情况(Is=9.0 μA/cm2)Fig.3 Maximum Lyapunov exponents λ as a function of K while parameter d varied(Is=9.0 μA/cm2)

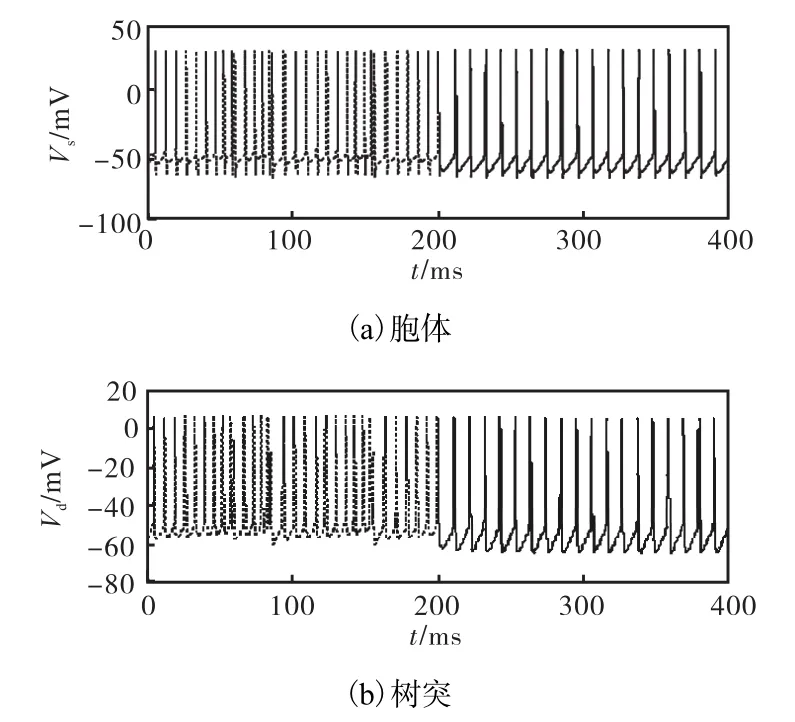
图4 Is =9.0 μA /cm2，K =0.3和 d =0.4时神经元的放电时间序列(控制项在t=200 ms时加入)Fig.4 Time series of ghostburster model with I s =9.0 μA /cm2，K=0.3 and d=0.4 (t=200 ms)

图 5 加入控制器(参数为 0.3K= ， 0.4d= )后 ghostburster模型状态随着去极化电流 sI变化的分岔图Fig.5 Bifurcation diagram of fand λafter adding controller with 0.3=K ，0.4=d

2.2.2 从周期放电到混沌簇放电或其他放电模式的转迁

在极限环的鞍结分岔点左方取 Is= 8 .0μA /cm2．为分析方便仍然取 d = 0 .4．图 6给出了在 K =−0 .2、K=−1 .0和 K =−2 .0时胞体的动作电位．控制项在t= 1 00ms时加入．随着K减小，神经元先是转变成周期簇放电，然后再转变成高频峰放电．在混沌区域内，λ剧烈波动．通过λ的变化确定系统混沌时K的取值范围．当d=0.4时，K的取值在[−0.8,0]之间．随着d的增加，K的取值范围也在增加．图7(b)图．因为 pd对快子系统的直接作用对象是树突膜电压 Vd，为分析方便选择 Vd作为快子系统的代表变量进行研究．分岔图顶部带三角形标志实线为在不同pd下 Vd在周期轨道上的极大值． pd= pd1是快子系统将 -Kd平面( 0K＜ )划分成2部分，神经元在该平面上半部分呈混沌簇放电状态，在下半部分呈周期簇放电状态．所以，K为负时可以达到将周期放电转换为混沌簇放电或高频放电的目的．

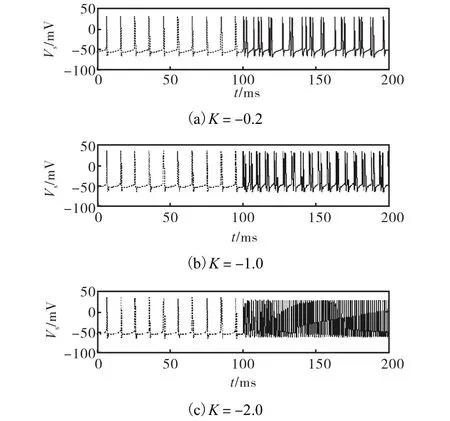
图 6 不同的 washout控制参数下胞体的放电时间序列(Is＝8.0 μA/cm2，d＝0.4，控制项在 t＝100 ms时加入)Fig.6 Membrane potential of soma before and after control with different parameters (Is＝8.0,μA/cm2，d＝0.4，and t＝100 ms)

图7 不同控制参数下放电模式的区域划分Fig.7 Regions of firing patterns divided by different control paramters

2.3 Washout滤波器对 ghostburster模型的作用机制分析

为了分析washout滤波器对ghostburster模型分岔点的作用机制，利用奇异摄动理论[22-23]，将ghostburster模型分成一快一慢2个子系统，表示为

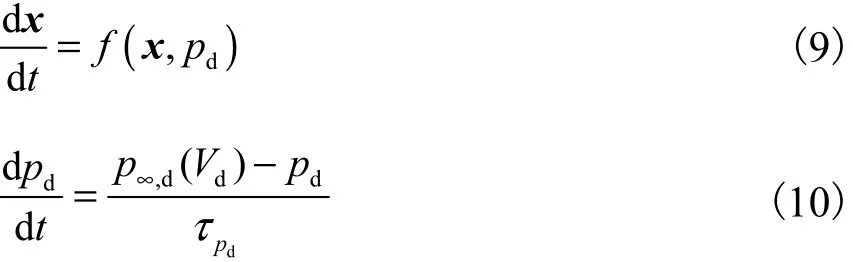
式中x为快变量的向量．在原始系统中，该向量包含了 Vs、Vd、ns、hd和 nd5个变量．因为 washout滤波器的常数大约为2.5 ms(1d)，约为τpd的一半，所以washout滤波器变量z也应为快变量．在快子系统变化过程中 pd可以近似为常数，所以其为慢变量． f ( x , pd)在原始模型中表示的是式(1)～式(5)，而在控制模型中表示的是式(1)～式(5)和式(7)．

2.3.1 从混沌簇放电到周期放电转迁的情况

图 8 对于延后鞍结分岔点的快慢系统分析( Is= 9 .0μA /cm2，K= 0 .3， d = 0 .4)Fig.8 Analysis of fast-slow subsystem in the case of delaying bifurcation point( I s = 9 .0 μ A /cm2,K = 0 .3,d = 0 .4)

图 8(a)是当 Is= 9 .0μA /cm2时快子系统的分岔周期一极限环和周期二极限环的分界点．在 pd＞pd1时 Vd只有 1个极大值，而在 pd＜pd1时有2个极大值．分岔图中部带方块标志实线为 2个连续放电之间 Vd的平均值 Vd，表示为式中 ti是第i个放电的放电时间．树突膜电压 Vd在pd＜pd1时呈二周期簇放电状态，其第2个放电的峰值减小，和下一个放电之间的时间间隔拉长．所以Vd在pd= pd1处也出现了一个明显的拐点．分岔图底部带空心圆点的长虚线 d pdd t = 0 为 pd零值线，其和 Vd曲线交于 pd= pd2＜ pd1，在该点处由正变负．在 pd=(= 2 .207749＞ pd1)处快子系统出现了固定点的鞍结分岔．因为 pd是钾离子通道的失活变量，增加 pd相当于减小去极化电流 Is．

把全系统的解投射到 Vd-pd相平面上(图 8(b)中带箭头的实线)来分析簇放电的产生过程．假设解轨迹从位于 pd零值线下方的 A 点出发，因为dpddt ＞ 0 ，轨迹向右边缓慢移动．在穿过 pd零值线后，由于 d pdd t ＜ 0 ，轨迹向左移动并突然产生一次放电上跳至 Vd最大值曲线的某一点．之后，受复极化变量 hd的作用，Vd下落跌回 pd零值线的下方．Vd-pd轨迹盘旋左移远离固定点的鞍结分岔点 pd=，放电频率也逐渐增加．在进入 pd(t)＜pd1区域以后，轨迹从周期一峰放电转换成周期二峰放电，这是一次高频二次放电，第 2次放电的幅值会减小从而使 Vd减小．当，p (t)重新增加逐渐d进入“诡异的”鞍结分岔点． pd越接近，移动也就越缓慢，所以簇放电之间的间隔拉长．这种簇放电是混沌的，具有不可重复性，其产生取决于解轨迹能否从周期一区域进入周期二区域从而产生不完全的放电[18]．

图8(c)是加上washout滤波器反馈控制(参数为d= 0 .4， K = 0 .3)以后快子系统的分岔图．当dpddt = 0 时，pd由 Vd唯一确定，所以 pd零值线和图8(a)相比没有变化．通过对比还可以发现 pd1左移而pd2右移，它们相互靠近使 Vd-pd轨迹进入周期二区域越来越难． pd1和 pd2越靠近，产生不完全的放电就越困难．解轨迹向右移动，而固定点的鞍结分岔并没有变化． pd在进入 pd(t)＜pd1区域之前返回高值区域，在这种情况下产生簇放电的条件并不满足．所以系统只能产生周期放电(图 4(a)和(b)，t = 2 00ms 后部分)．

2.3.2 从周期放电到混沌簇放电或其他放电模式的情况

图 9(a)是当 Is= 8 .0μA /cm2时，原系统的快子系统分岔图及全系统解在 Vd-pd平面上的投影叠加到分岔图上的情形，pd1和 pd2的距离和图 8(a)相比缩短了，而固定点的鞍结分岔= 1 .472756则更接近pd1．在 pd1，pd2和相互作用下，解轨迹被夹在 pd1和之间，系统周期放电．

图 9(b)为当 washout滤波器参数为 d = 0 .4，K=− 0 .2时快子系统的分岔图．和图 9(a)相比，固定点的鞍结分岔保持不变，但是 pd1的位置右移而pd2左移，两者距离拉长使解轨迹易于进入周期二区域，所以，整个轨迹向左移动，系统呈混沌放电状态(图6(a)，t = 1 00ms后部分)．继续减小washout滤波器的参数K(图 9(c)，K =−1 .0)，pd1和解轨迹都继续左移，而 Vd曲线上升，和 pd零值线不再具有交点．全系统只能产生一个完全放电和一个不完全放电，呈周期二簇放电状态(图 6(b)，t = 1 00ms 后部分)．进一步减小K( K=−2 .0)时(图 9(d)～(f))，pd1和之间的距离继续减小，周期二区域右移．在图 9(d)中 Vd,max左端，快子系统从右到左经历了一次从周期二极限环到周期一极限环的转换过程，其临界点记为 pd2．为简单起见，把加入控制器以前，加入控制器以后的过渡阶段和稳定阶段的解轨迹分别叠加到分岔图上．从图 9(d)可知轨迹是周期的，但是在washout滤波器加入以后，解轨迹马上远离固定点的鞍结分岔．周期二区域同时右移把解轨迹包含在内．因为解轨迹不能马上变化，它只能盘旋左移产生不完全的放电并穿越 pd2图9(e)．在 pd＜pd2时，解轨迹逐渐收敛成一个极限环(图 9(f))．所以，树突膜电压呈高频小幅震荡状态，而在胞体则体现为高频峰放电．

综上所述，外电流的加入改变了 Ghostburster模型快子系统从周期一极限环转换到周期二极限环的临界点 pd1，树突平均模电压的正负分界点 pd2和快子系统固定点的鞍结分岔的位置．而 washout滤波器只改变 pd1和 pd2的位置．考虑到 pd2并不总是存在(如图9(c) 和(d)的情况)，可以得出washout滤波器通过影响 pd1产生树突的不完全放电，从而影响整个ghostburster神经元是否产生簇放电的结论．

图9 对于提前鞍结分岔点的快慢系统分析( Is=8.0μA /cm2，d=0.4)Fig.9 Analysis of fast-slow subsystem in case of advancing bifurcation point( I s=8.0μA /cm2，d=0.4)

3 结 语

将 washout滤波器作为反馈控制器加入到ghostburster模型中以实现极限环上的鞍结分岔点附近的放电模式转换．然后，通过把系统分成快慢 2个子系统，研究了 washout滤波器作用于 ghostburster模型的机制．因为washout滤波器并不改变系统平衡点(包括全系统和快子系统)的位置，所以其通过改变从周期一极限环转换到周期二极限环的临界点的位置来实现放电模式的转迁．而外加电流除了改变上述分岔外，还可以改变快子系统固定点的鞍结分岔．本文的研究明确了 ghostburster模型的簇放电形成机制．在以后的研究中会继续探讨鞍结分岔控制对神经系统的作用机制，以期为神经系统疾病诊断和治疗提供参考．

［1］ Izhikevich E M. Dynamical Systems in Neuroscience：The Geometry of Excitability and Bursting[M]. Cambridge：The MIT Press，2007.

［2］ 杨卓琴，陆启韶. 神经元 Chay模型中不同类型的簇放电模式[J]. 中国科学，2007，37(4)：440-450.Yang Zhuoqin，Lu Qishao. Different bursting patterns in chay neuron model[J]. Science in China，2007，37(4)：440-450(in Chinese).

［3］ 杨卓琴. 神经元电活动不同节律模式的几种变化过程[J]. 物理学报，2010，59(8)：5319-5324.Yang Zhuoqin. Transitions of different rhythm patterns of neuronal firing activity[J]. Acta Phys Sin，2010，59(8)：5319-5324(in Chinese).

［4］ 王宝燕，徐 伟，邢真慈. 外界电场激励下的耦合FitzHugh-Nagumo神经元系统的放电节律研究[J]. 物理学报，2009，58(9)：6590-6595.Wang Baoyan，Xu Wei，Xing Zhenci. Fire patterns of coupled FitzHugh-Nagumo neurons exposed to external electric field[J]. Acta Phys Sin，2009，58(9)：6590-6595(in Chinese).

［5］ Rubin J E，Terman D. High frequency stimulation of the subthalamic nucleus eliminates pathological thalamic rhythmicity in a computational model[J]. J Comput Neurosci，2004，16(3)：211-235.

［6］ Terman D，Rubin J E，Yew A C，et al. Activity patterns in a model for the subthalamopallidal network of the basal ganglia[J]. J Neurosci，2002，22(7)：2963-2976.

［7］ Singer W，Gray C M. Visual feature integration and the temporal correlation Hypothesis[J]. Annu Rev Neurosci，1995，18：555-586.

［8］ Wehr M，Laurent G. Odour encoding by temporal sequences of firing in oscillating neural assemblies[J]. Nature，1996，384(14)：162-166.

［9］ Singer W. Synchronization of cortical activity and its putative role in information processing and learning[J].Annu Rev Neurosci，1993，55(3)：349-374.

［10］ Chen G R，Moiola J L，Wang H O. Bifurcation control：Theories，methods，and applications[J]. Int J Bif and Chaos，2000，10(3)：511-548.

［11］ Schiff S J，Sauer T. Kalman filter control of a model of spatiotemporal cortical dynamics[J]. J Neural Eng，2008，5(1)：1-8.

［12］ Munoz L M，Stockton J F，Otani N F. Applications of control theory to the dynamics and propagation of cardiac action potentials[J]. Annals of Biomedical Engineering，2010，38(9)：2865-2876.

［13］ Xie Y，Chen L N，Kang Y M，et al. Controlling the onset of Hopf bifurcation in the Hodgkin-Huxley model[J]. Physical Review E，2008，77(6)：061921.

［14］ Wang J，Chen L Q，Fei X Y. Bifurcation control of the Hodgkin-Huxley equations[J]. Chaos，Solitons & Fractals，2007，33(1)：217-224.

［15］ 罗 明，彭建华，吴勇军. Washout-filter辅助的FitzHugh-Nagumo神经元放电行为的分岔控制[J]. 动力学与控制学报，2009，7(3)：226-229.Luo Ming，Peng Jianhua，Wu Yongjun. Bifurcation control of FitzHugh-Nagumo neuronal firing behabior aided with Washout-filter[J]. Journal of Dynamics and Contrrol，2009，7(3)：226-229(in Chinese).

［16］ Wang H O，Abed E H. Bifurcation control of a chaotic system[J]. Automatica，1995，31(9)：1213-1326.

［17］ Zhou S B，Liao L F，Wu Z F，et al. Washout filterbased chaotic control in a neural network with uncertain time delays [C]//Proceedings of International Conference on Communications，Circuits and Systems. Hong Kong，China，2005：959-963.

［18］ Doiron B，Laing C R，Longtin A. Ghostbursting：A novel neuronal burst mechanism[J]. J Comput Neurosci，2002，12(1)：5-25.

［19］ Laing C R， Doiron B， Longtin A， et al.Ghostbursting：The effects of dendrites on spike patterns[J]. Neurocomp，2002，44(3)：127-132.

［20］ Lemon N，Turner R W. Conditional spike backpropagation generates burst discharge in a sensory neuron[J].J Neurophysiol，2000，84(3)：1519-1530.

［21］ 赵益波，罗晓曙. 基于washout滤波器技术的Colpitts振荡器混沌控制研究[J]. 物理学报，2007，56(11)：6258-6262.Zhao Yibo，Luo Xiaoshu. Study on chaotic control of Colpitts oscillator based on washout filter technique[J].Acta Phys Sin，2007，56(11)：6258-6262(in Chinese).

［22］ Guckenheimer J. Progress in Nonlinear Differential Equations and Their Applications[M]. Boston：Birkhauser，1996.

［23］ Rinzel J，Lee Y S. Nonlinear Oscillations in Biology and Chemistry[M]. New York：Springer，1986.