面向芯片引线键合的视觉精确定位方法
李君兰 ,刘士为,张大卫
(1. 清华大学精密仪器与机械学系,北京 100084;2. 天津大学机械工程学院,天津 300072)
引线键合技术是目前应用最广泛的一种芯片互联技术,在集成电路制造行业中有着重要的用途.随着半导体制造业的发展,对引线键合的速度和精度都提出了更高的要求,单纯依靠提高运动控制精度来提高引线键合的速度和精度已不能满足需要.因此视觉系统成为影响焊线速度和精度的重要因素之一[1-2].
面向引线键合的视觉定位过程为通过视觉系统获取芯片及其引线框架的图像,计算图像相对预先定义的标准位置的偏差值,从而得知芯片和引线框架相对于标准图像的位置坐标和转角误差,在键合时通过二者的相对位置修正运动平台和键合头的工作位置,实现高精度的焊线[2].本文中所讨论的引线键和工艺上的芯片需要满足一定的精度要求,约为±0.015,mm.
芯片和引线框架的定位过程为现有的视觉定位方法大致可分为基于灰度的方法和基于特征的方法两类.基于灰度方法的代表是模板匹配技术,这种技术已经被应用到了 IC芯片封装设备中[4],然而这种方法运算量大,受照明灯条件的影响大,且在图像具有较大旋转角度时无法得到满意的定位结果.Berthilsson[5]和 Simper[6]用分布求解使灰度互相关法,对具有投影变换关系和镜头变形的图像进行匹配.但是该方法的计算量很大,因此实时性较差.Hiroi等[7]提出了差值平方和算法检测 2幅图像间的平移,这种方法可以获得亚像素级的定位精度,但只适用于微小的平移定位.此外,序贯相似性判决算法由于具有运算速度较快的优点,也被应用在面向芯片封装的视觉定位中[8].
基于特征的方法是目前的研究热点.叶其春等[9]在点相关算法的基础上进行了改进,并引入到芯片封装的视觉定位中,这种方法使定位精度及抗噪性方面都得以改善,但需要预定义点集,对特征点的提取精度和准确性要求较高,易造成误匹配.小波变换在面向芯片封装的视觉定位算法中的应用,可以清晰地提取芯片焊点特征,并与其他算法(如径向基函数网络算法[10])相结合,获得高精度的定位结果,但对于复杂的芯片图像小波算法运算量大,且需要其他算法的辅助.目前,面向引线键合的视觉定位算法大多针对芯片的图像而进行研究,主要集中在芯片焊点及相关特征的提取上[8-10],而对芯片引线框架图像的定位方法研究甚少.
综上所述,笔者的面向引线键合的视觉定位方法,分别针对芯片和引线框架图像的特点提出高速高精度的视觉定位算法,对于芯片图像使用基于傅里叶变换的图像匹配算法进行定位,对于引线框架的图像使用基于几何不变矩的方法进行定位.这2种方法结合能够有效的实现引线键合中的视觉精确定位.
1 视觉定位算法
1.1 基于快速傅里叶互相关的图像定位算法
首先将模板图像 T和待定位图像 I进行二维离散傅里叶变换(discrete Fourier transform,DFT),模板图像和待定位图像的DFT可以分别表示为

式中:T(,)Fξη、I(,)Fξη分别为模板图像 T和待定位图像I的DFT变换;M、N为图像模板为T的大小;J、K为待定位图像的大小;ξ和η分别为x和y方向上的频率变量,且

由相关定理可写出相关的离散傅里叶变换为
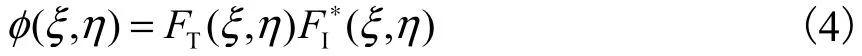
式中I(,)Fξη∗表示T(,)Fξη的复共轭.对(,)φξη求傅里叶反变换,得到空间域的相关函数为
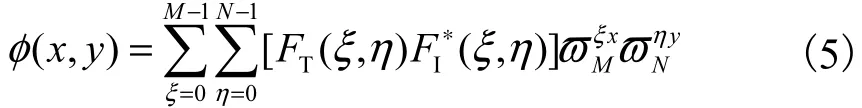
在计算离散傅里叶变换时使用 FFT算法[11],可以得到比直接计算空间域的互相关函数更快的运算速度.FFT相关算法示意如图1所示.
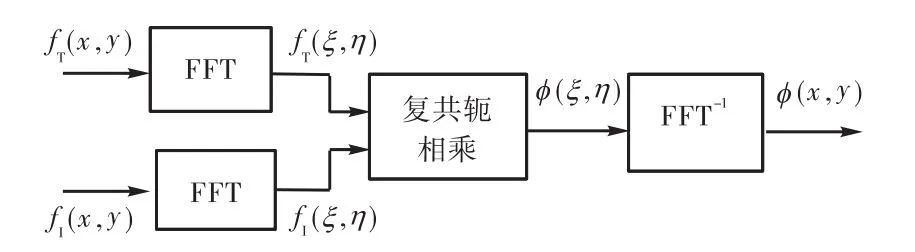
图1 FFT相关算法示意Fig.1 Schematic diagram of FFT correlation algorithm
假设 2幅图像间只有相对的位移 ( x0,y0),则2幅图像间的相互关系为
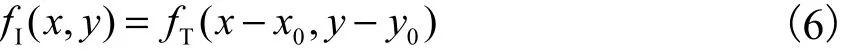
傅里叶变换后2幅图像间的关系可以表示为

若 MT(ξ,η)和 MI(ξ,η)分 别 表 示 FT(ξ,η) 和FI(ξ,η)的幅值,则有

2幅图像在频域的互功率谱定义为
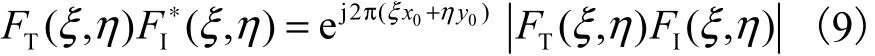
由式(5)可知,若对频域的互功率谱进行傅里叶反变换,则可以得到空间域的互相关函数,而相关函数的值在最佳匹配位置出现峰值,而在其余位置几乎为 0.在计算时记录互相关函数出现峰值时的像素位置即为最佳匹配位置,而此时的位移 ( x0,y0)即为2幅图像间的位移.
同理,若 2幅图像间有相对的位移 ( x0,y0)和转角θ0,则2幅图像间的相互关系为

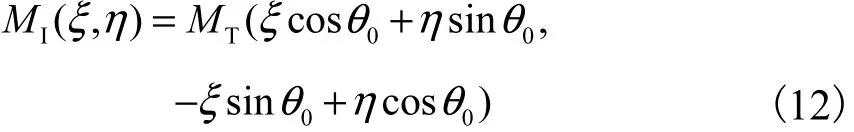
由式(12)可知,2幅图像傅里叶变换后的幅值只与转角有关,而与位移无关.仅存在转角时,2幅图像间的互相关可以用极坐标表示为

此时,对其进行傅里叶反变换,同样可以获得最佳匹配时的转角值.
1.2 基于不变矩的图像定位算法
基于特征的视觉定位方法往往采用图像的轮廓作为特征进行匹配定位[12],然而这种方法需要获得很高精度的图像边缘信息.由于图像边缘提取的过程必定会造成一定的误差,因此获得更高精度的边缘需要进行插值等计算,大大增加了运算时间,不能满足引线键合的快速性要求.因此提出一种使用几何矩计算特征区域矩心和转角,并使用不变矩[13]进行匹配,从而实现使用图像中的特征进行定位的方法.
一幅二维图像的p q+ 阶矩定义为

式中:x、y为像素的坐标值; f(x,y)为像素的灰度值.
图像灰度的矩心坐标(x,y)反映了图像区域的几何中心,其计算式为

根据图像的矩心坐标(x,y)可定义图像的中心矩,它反映了图像灰度相对于矩心的分布情况,表示为
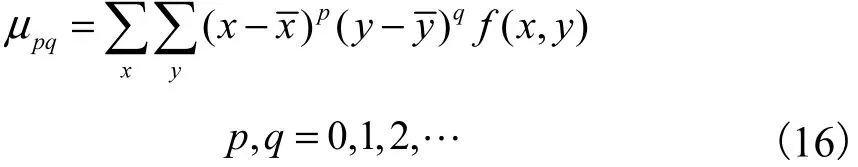
如图 2所示,图中的特征区域相对于整幅图像的方位角γ能够反映特征相对于图像的转角,而特征区域在图像中的矩心坐标反映了特征在图像中的位置.坐标轴x′称为本原坐标轴,为穿过图像矩心O的2条正交线,转角 γ为图像本原坐标轴之一 x′相对于图像x轴的方位角.本原坐标系与图像坐标系之间的变换关系可表示为
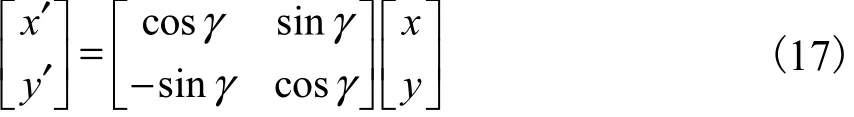
令pqμ′表示本原坐标轴下的中心矩,则有等式
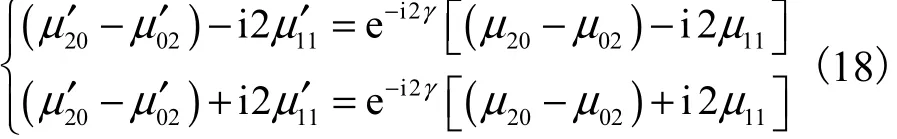

图2 旋转角度γ 示意Fig.2 Schematic diagram of rotation angle γ
在本原坐标系中,灰度分布的协方差110μ′=,因此由式(18)可以求得转角γ的值为
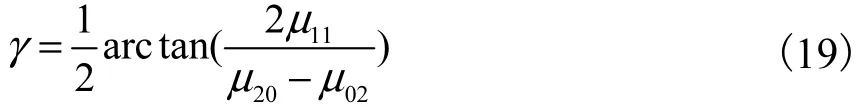
在实际进行视觉定位的过程中,会出现一幅图像中存在多个特征的情况,因此匹配定位时需要确定特征区域的对应关系.考虑到运算量和准确性的要求,引入不变矩寻找特征之间的对应关系.对式(16)所定义的pq+阶中心矩pqμ进行规范化,即

式中r为0阶中心矩00μ的指数2,3,…).
规范化的p q+ 阶中心矩经过组合得到 7个不变距,也称为Hu矩,即

经证明这7个矩具有平移、旋转及尺度不变性,作为图像的特征描述子.而判断 2个特征之间的相似性的公式为

整个的视觉定位过程可以归纳为:先经过特征提取获得图像中的特种区域,经过对特征区域矩心和转角的计算获得位置和旋转坐标;在图像中存在多个特征区域时,使用不变矩寻找对应的特征;相同的特征进行比较,确定整个引线框架的位置坐标和转角值.
2 视觉系统硬件及图像
实验使用的显微视觉系统包括:JAI CV-A1 CCD摄像机,Navitar Zoom 6000显微镜头,红光LED环形光源,NI PCI-1409图像采集卡和实验台架.二维运动平台采用赵兴玉等[14]设计的由音圈电机驱动的精密定位平台.实验系统的照片如图3所示.

图3 视觉系统实验照片Fig.3 Experimental picture of vision system
图 4为使用视觉系统获取的芯片和引线框架图像.芯片图像(图 4(a))中的特征较复杂,特征提取时可经过小波变换或者形态学处理等方法得到焊点特征,但处理过程费时且对特征的位置精度影响较大,从而也会对定位精度造成影响.而引线框架图像(图4(b))中的特征明显,因此通过特征提取能够得到精度较高的特征信息,此时使用提取出的特征进行定位能够获得较好的定位精度.因此,根据图像的特点,为了提高视觉定位过程的精度和效率,使用快速傅里叶变换的方法对芯片图像进行定位,使用不变矩的方法对引线框架图像进行定位,可实现面向引线键合的视觉精确定位.

图4 芯片和引线框架图像Fig.4 Chip and leadframe images
3 视觉定位实验及结果
3.1 芯片定位实验
使用 Matlab软件编写了算法程序,并使用一种芯片对傅里叶变换算法进行了实验.实验结果如图 5所示.首先在第 1幅芯片图像中选取模板区域,即图5(a)中的方框区域,然后在第 2幅图像中进行搜素,得到与模板匹配度最高的图像区域(图5(b)).

图5 对芯片区域的定位实验结果Fig.5 Localization results of chip
使用多幅图像进行了多次实验,实验表明匹配定位误差在 0.4像素(<2,μm)以内,能够满足芯片封装的精度要求.其优点在于:由于采用了傅里叶变换和反变换,与一般的灰度定位法相比定位精度更高,运算速度较灰度互相关算法更快,从而能够提高芯片定位的精度和效率.且这种方法不受芯片种类的影响,通用性好,受噪声的影响小.
3.2 引线框架的定位实验结果
3.2.1 特征提取
在对图像进行定位之前,需要对图像进行一系列的处理,以获得需要的特征区域.对引线框架引脚的图像进行图像处理的过程如图 6所示.引线框架引脚的图像经过 Canny边缘提取(图 6(b))、边缘跟踪(图 6(c))、对封闭轮廓进行提取(图 6(d))以及图象分割(图 6(e))后,获得图像中的特征区域,这些特征区域即可用做基于不变矩的定位.
3.2.2 定位结果
分别对图像做一定的平移和旋转,得到一组的引线框架的图像,对图像进行特征提取,并使用几何矩计算位移值和转角值,进行匹配并分析误差.图 7为具有相对位移和旋转的 2幅图像的匹配定位结果.定位误差分析结果如表1~表3所示.

图6 定位前的图像特征提取过程Fig.6 Image processing before localization

图7 2幅引线框架图像的匹配定位Fig.7 Localization of two leadframe images

表1 芯片定位的位移计算结果及误差分析Tab.1 Results and error analysis of chip’s translations

表2 引线框架视觉定位的位移计算结果及误差分析Tab.2 Results and error analysis of leadframes’ translations

表3 引线框架视觉定位的转角计算结果及误差分析Tab.3 Results and error analysis of leadframes’ rotations
实验结果表明:基于不变矩的芯片定位方法具有运算速度快,且定位精度高的优点,同时能准确地获得芯片的位置和转角信息.位移坐标的定位精度小于 0.5像素(2.3,μm),转角的定位精度小于 0.1°,均能满足芯片封装的要求.由于采用的是特征区域进行匹配,因此抗噪声的能力好.
4 结 论
(1) 针对芯片的傅里叶变换定位方法能够有效地对芯片区域的图像进行定位,定位精度在亚像素级,满足芯片封装的要求.
(2) 针对引线框架引脚的匹配定位采用基于特征的不变矩的定位方法,位置定位精度在亚像素级,转角定位精度在十分之一度,精度高运算速度快,能够提高引线键合的加工效率和精度.
(3) 以上2种方法结合,可在引线键合过程中快速有效地对芯片和引线框架进行视觉定位,从而实现对引线键合过程的视觉精确定位.
[1] Li Junlan,Wang Yizhong,Zhang Dawei,et al. Design and simulation of the positioning system using computer wision for IC packaging[J]. Journal of Shanghai Jiao Tong University,2008,13(suppl. ):91-95.
[2] 李君兰,张大卫,王以忠,等. 面向封装的显微视觉定位系统[J]. 光学精密工程,2010,18(4):965-972.Li Junlan,Zhang Dawei,Wang Yizhong,et al. Microvision positioning systems for IC packaging[J]. Optics and Precision Engineering,2010,18(4):965-972(in Chinese).
[3] Zitova B,Flusser J. Image registration methods:A survey[J]. Image and Vision Computing,2003,21:977-1000.
[4] Manickam S,Roth S D,Bushman T. Intelligent and optimal normalized correlation for high speed pattern matching[J]. Electrical and Electronic Engineering,2000,1:191-206.
[5] Berthilsson R. Affine correlation[C]// Proceedings of the International Conference on Pattern Recognition ICPR’.Brisbane,Australia,1998:1458-1461.
[6] Simper A. Correcting general band-to-band misregistrations[C]//Proceedings of the IEEE International Conference on Image Processing ICIP’. Lausanne ,Switzerland,1996:597-600.
[7] Hiroi T,Maeda S,Kubota H,et al. Precise visual inspection for LSI wafer patterns using subpixel image alignment[C]//Proceedings of the Second IEEE Workshop on Applications of Computer Vision. Florida,USA,1994:26-34.
[8] 姜永军,吴小洪,何汉武,等. 图像识别系统在 IC封装设备中的应用[J]. 半导体技术,2005,30(1):46-49.Jiang Yongjun,Wu Xiaohong,He Hanwu,et al. Use of pattern recognition system in IC package equipment[J]. Semiconductor Technology,2005,30(1):46-49(in Chinese).
[9] 叶其春,朱利民,丁 汉. 基于点相关的亚像素级图像匹配算法[J]. 机械与电子,2005(3):3-6.Ye Qichun,Zhu Limin,Ding Han. A point correlation based subpixel image registration algorithm[J]. Machinery and Electronics,2005(3):3-6(in Chinese).
[10] 昇汪宏 ,熊 飞,史铁林. 高速高精度的机器视觉定位的算法[J] 光电工程,2005,32(9):71-74.Wang Hongsheng,Xiong Fei,Shi Tielin. New algorithm for fast and precise localization of machine vision[J]. Opto-Electronic Engineering,2005,32(9):71-74(in Chinese).
[11] Reddy B S,Chatterji B N. An FFT-based technique for translation,rotation,and scale-invariant image registration[J]. IEEE Transactions on Image Processing,1996,5(8):1266-1271.
[12] Li Z,Leung H. Contour-based multisensor image registration with rigid transformation[C]//2007 10,th International Conference on Information Fusion. Canada,2007:1-7.
[13] Hu M. Visual pattern recognition by moment invariants[J]. IRE Transactions on Information Theory,1962,8(2):179-187.
[14] 赵兴玉,冯晓梅,武一民,等. 面向MEMS制造的高速精密定位平台的动力学仿真和结构设计[J]. 机械工程学报,2006,42(8):114-119.Zhao Xingyu,Feng Xiaomei,Wu Yimin,et al. Dynamic simulation and design of high speed precision positioning table[J]. Chinese Journal of Mechanical Engineering,2006,40(2):114-119(in Chinese).

