基于空间直角坐标系高精度坐标转换系统的设计①

郭英起，张秋江，韦昌胜，张为成，黑 龙

（1.黑龙江工程学院测绘工程学院，黑龙江 哈尔滨150050；2.黑龙江省第三森林调查规划设计院，黑龙江 哈尔滨150000；3.哈尔滨兰诺数码有限公司，黑龙江 哈尔滨150008）

0 引 言

随着卫星定位技术的发展和广泛应用，在国防建设、城市建设和各项工程建设中利用GNSS定位技术建立各种用途控制网已经相当普及［1－2]。坐标系统转换是城市建设、国防建设和各项工程建设中建立卫星控制网时经常遇到的问题。由于平面坐标转换模型是线性的、没有顾及高斯投影变形误差，只适合在较小区域范围内使用［3]。三维空间直角坐标转换是一种广为重要的使用方法。这是因为其不仅适合大中小区域，尤其在大区域内进行坐标系转换时能够保证最终转换结果的精度。

三维空间直角坐标转换大多利用布尔沙（Bursa）七参数转换模型，模型中包含三个平移参数、一个尺度比参数和三个旋转参数。转换参数具有时间性和区域性［4]，这就使得坐标转换参数的解算在实际测量工作中相当繁琐，许多城市建设和各项工程建设中对坐标转换精度的要求也越来越高。研制基于空间直角坐标系高精度坐标转换系统是非常必要的。

基于空间直角坐标系高精度坐标转换系统的设计思想、软件设计以及可靠性等内容进行阐述。

1 高精度坐标转换系统介绍

1.1 系统的设计思路

在三维空间直角坐标系利用布尔沙（Bursa）七参数转换模型进行坐标转换时，先要利用所选择公共点的双重坐标解算坐标转换参数。以往通常是利用经典最小二乘法进行解算。根椐现代平差理论，经典最小二乘法不具有抗干扰性，抵抗粗差的能力差［5]。如果所选择使用的公共点中某个或多个点精度较低或误差过大，势必会影响转换参数的解算精度。最终影响对控制点进行坐标转换的精度。

利用经典最小二乘法解算坐标转换参数，并利用获得的转换参数对公共点进行坐标转换，而转换后的坐标与公共点原坐标差值的大小会很直观地反映出转换参数精度的好坏。因为如果解算坐标转换参数时所选择的公共点中某个点精度较低或误差过大时，对该公共点进行坐标转换后其坐标差值会相对较大。当对公共点进行坐标转换后一个或多个点其坐标差值较大时，即可以认为该公共点的坐标精度较低或误差过大。根据稳健抗差估计理论，可以对精度较低或误差过大的公共点进行重新定权，即按照稳健抗差估计理论重新确定其等价权矩阵，逐渐降低其在转换参数解算中的作用，并在依次的解算中最后确定高精度坐标转换参数，最终达到进行高精度坐标转换的目的。

1.2 系统的界面结构

本系统采用目前比较流行的面向对象的程序设计语言C＃进行开发编制，程序语言简单易懂，由C和C＋＋派生而来，继承了强大的功能，同时以NET框架类库作为基础，提供开发人员快速的开发手段，快捷地构建系统。本系统界面如图1所示。

图1 高精度坐标转换系统界面图

系统的界面分成如下几个部分：

左上方为已知数据框，已知数据可以通过键盘输入，亦可以通过提前在记事本上建立的.dat文件导入。已知数据包括所要选择的公共点双重坐标和要进行坐标系统转换的所用控制点坐标。左边中间框为利用所选择的公共点双重坐标解算坐标转换参数的过程数据。

左下方为坐标转换框，是利用经解算最后确定的坐标转换参数对所有控制点的坐标进行转换的结果。其中包括所有控制点的原坐标和转换后的坐标情况。右上方为坐标转换参数框，其包括所解算的七个坐标转换参数具体数值。右边中间有五个控制键，第一个键代表利用经典最小二乘法解算坐标转换参数。第二个键代表利用稳健抗差估计理论解算坐标转换参数，当发现所选择的公共点双重坐标坐标精度较低或误差过大时使用。第三个键代表设置的值，在利用稳健抗差估计理论解算坐标转换参数时，通过选择适当的值，可以剔除含有粗差的控制点，避免其参与坐标转换参数的解算。第四个键代表设置的值，在利用稳健抗差估计理论解算坐标转换参数时，通过选择适当的值，确定坐标精度较低或误差过大的公共点，并对其进行重新定权。第五个键代表设置的容差值，在利用稳健抗差估计理论解算坐标转换参数时，通过选择适当的容差值，确定迭代计算的次数，并以最后一次解算的坐标转换参数为最后估值。右边下方设置了计算方法选择键以及成果输出键等。

1.3 系统的功能

基于三维空间直角坐标系高精度坐标转换系统主要具有如下几个功能：

1）能够发现坐标中含有粗差的公共点，并强行剔除其参加坐标转换参数的解算。

2）能够利用经典最小二乘法解算坐标转换参数，并对所有控制点的坐标进行转换。

3）能够利用稳健抗差估计理论解算高精度坐标转换参数，并对所有控制点的坐标进行高精度转换。

4）能够在一定程度上纠正坐标精度较低或误差过大的公共点坐标中的误差，转换后能够使其坐标趋近于正确值。

1.4 系统的特点

基于三维空间直角坐标系高精度坐标转换系统具有如下几个特点：

1）界面简单、清晰、友好，便于操作和使用。

2）功能较全，可以做多功能选择。

3）读入已知数据和输出成果时方便、快捷。

4）可适用于在任意两个空间直角坐标系统间进行坐标转换。

2 算例分析

现有一GPS控制网，平差后获得各点在WGS－84坐标系和GDZ80坐标系的坐标，现选择其中四个点的三维空间直角坐标列于表1中。

1）首先利用表中4个控制点的双重坐标，按经典最小二乘法解算，由 WGS－84坐标系到GDZ80坐标系的七个坐标转换参数为

ΔX＝20.164 746 81；ΔY＝ －13.290 487 81；

ΔZ＝ －11.321 662 18；εX＝2″.723 413；

εY＝ －3″.441 397；εZ＝0″.543 789；

k＝－0.000 002 700

利用这七个坐标转换参数对各控制点坐标进行转换，并求各点转换后的坐标与原坐标值之差列于表中的列｜Δ｜中。从计算结果数据可以看出，由于所用公共点坐标精度均较高，转换后坐标差值都为零。

2）当在p1点的坐标中人为地增加－5.2cm的误差（点位误差即为5.2cm）时。由于其点位误差大于5.0cm，可以认为该点含有粗差，当k1值取14时系统即将p1点强行剔除，避免其参加坐标转换参数的解算。

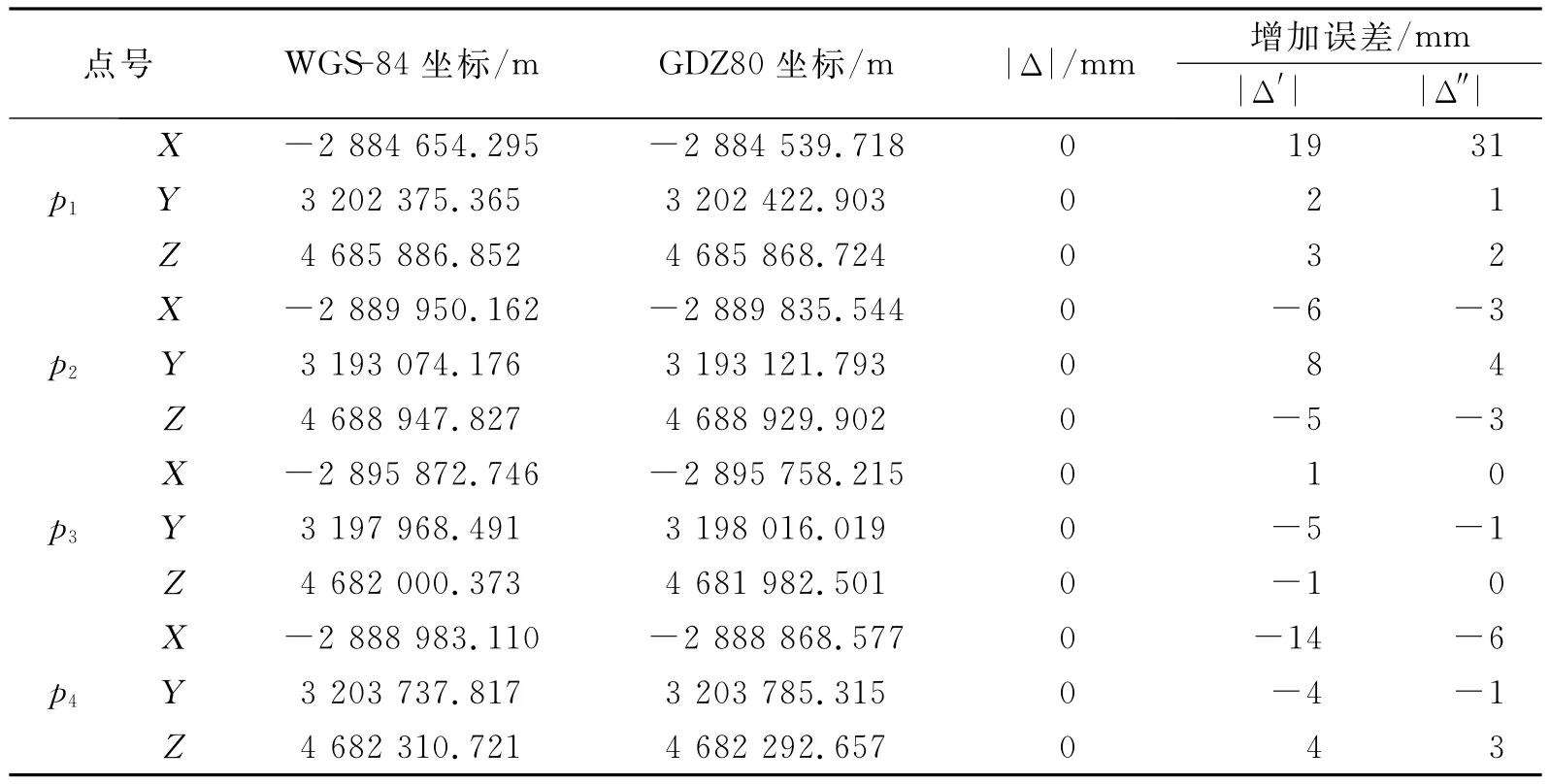
表1 各点于WGS－84系和GDZ80系坐标值及其转换后坐标差值

3）当在p1点的X坐标中人为地增加－4.0 cm的误差（点位误差即为4.0cm）时。由于其点位误差小于5.0cm可以认为该点不含有粗差，但其坐标精度较低或误差较大。现仍然按照经典最小二乘法解算七个坐标转换参数分别为

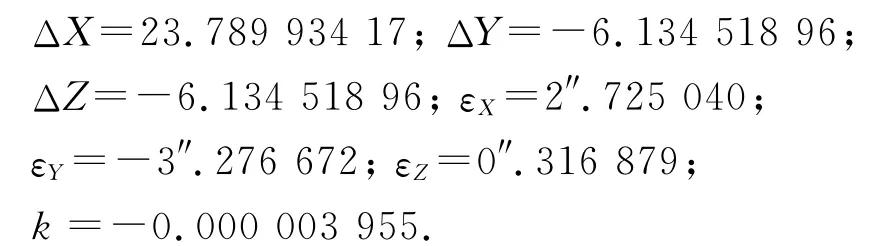
再利用这七个坐标转换参数对各控制点坐标进行转换，求各点转换后的坐标与原坐标值之差列于表中的｜Δ′｜列中。由于点坐标精度较低，各点坐标转换后的差值普遍增大，尤其是点的坐标转换后的坐标差值最大，比其他点的坐标差值大许多。

4）针对点坐标精度较低的问题，利用本系统中稳健抗差估计方法解算七个坐标转换参数为

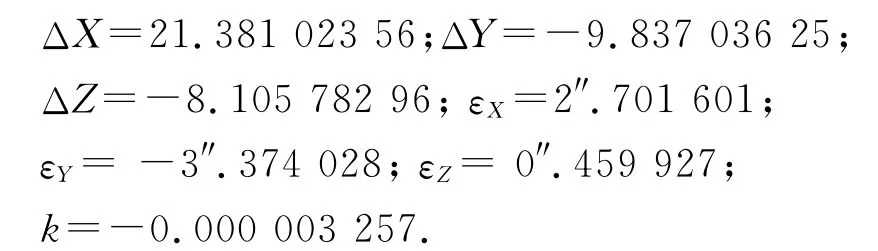
利用这七个坐标转换参数对各控制点坐标进行转换，将转换后坐标与原坐标差值列于表中的｜Δ″｜列中。除p1点外其它各点转换后坐标的差值都明显地变小了。而对于p1点的X坐标转换后坐标的差值虽然增大，却显示对于p1点转换后的坐标值相对于转换前含有误差的坐标值更接近于它的真值了，这就说明该方法具有明显的抗差作用，而且在很大程度上纠正p1点坐标中的误差。

3 结 论

阐述了利用面向对象的程序设计语言C＃设计基于三维空间直角坐标系高精度坐标转换系统软件的情况。该系统软件具有界面简单、便于掌握和使用；功能较全、能够做多样选择等特点。该系统软件可以在任意两个空间直角坐标系统间进行坐标转换。

［1]刘大杰，施一民，过静君.全球定位系统（GPS）的原理与数据处理［M].上海：同济大学出版社，1996.

［2]李征航，黄劲松.GPS测量与数据处理［M].武汉：武汉大学出版社，2007.

［3]王解先.七参数转换中参数之间的相关性［J].大地测量与地球动力学，2007，27（2）：43－46.

［4]黄声享，郭英起，易庆林.GPS在测量工程中的应用［M].北京：测绘出版社，2007.

［5]黄维彬.近代平差理论及其应用［M].北京：解放军出版社，1990.

［6]杨元喜，张丽萍.坐标基准维持与动态监测网数据处理［J].武汉大学学报·信息科学版，2007，32（11）：967－971.

［7]KOCH K R，YANG Yuan－xi.Robust Kalman filter for rank deficient observation Model［J].Journal of Geodesy，1998，72（8）：436－441.

［8]陈国建，游 梁，张建辉，等.C＋＋语言从入门到精通［M].北京：机械工业出版社，2011.