车载GNSS接收机多径抑制技术①

王振岭

（1.中国电子科技集团公司第54研究所，河北 石家庄050081；2.河北省卫星导航技术与装备工程技术研究中心，河北 石家庄050081）

0 引 言

车载GNSS接收机的伪距测量会受到很多误差因素的影响，其中，由多径影响所带来的误差幅度较大，在车载接收机使用环境下，多径会受到周边工作环境的影响而使其具有特殊性和时变性，也因此更加难以预测。尽管扩频技术自身对信号延迟较大的多径信号具有很好的抑制作用，而当多径延迟较小（典型值小于1chip）时，仍然会对伪距观测量产生很大影响。传统的通信系统对多径的考虑仅限于信号幅度的影响，而卫星导航系统则对信号延迟带来的影响更为关注。因此，面向车载GNSS接收机极其广泛的应用，其产品研制需要对多径抑制的实现予以重点考虑。

紧密结合车载GNSS接收机的应用特点，对多种多径抑制方法进行了介绍和分析比较，并给出结论。

1 车载GNSS接收机多径影响及特点

1.1 多径

多径描述的是一个卫星信号通过多个路径到

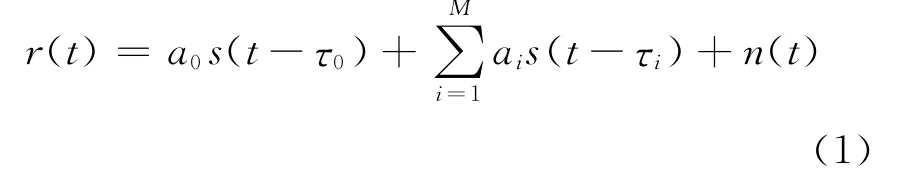
式中：s（t）为传输的信号；a0为直达信号的幅度；τ0是直达信号的时间延迟；n（t）为高斯白噪声；M是多径信号的个数；ai、τi分别为第i个多径分量的幅度和延迟。

图1给出了GNSS卫星到接收机的直达信号和非直达信号的传输原理示意图。可以看出，几何学环境是产生多径的主要因素，信号被周围建筑物、物体等的反射是产生多径的主要原因。

实际上，信号的反射还可以划分为散射和平面反射两类。散射是一种较大区域内分散的反射，其结果波形可使用多个不同幅度和相位的反射波之和进行描述。散射引起的多径效果符合Rayleigh分布［1]，但通常很难建模，在实际处理中一般按噪声处理。平面反射通常来自于天线附近的物体，该达接收机产生的影响。多径可以认为是系统的内部干扰，它包括来自天线的一条直达信号（直线）和多条间接信号（非直线信号）的叠加。假设天线接收到若干不同时刻和功率的传输复制信号，则可定义受到多径影响的卫星的接收信号为条件下的合成波形几乎没有相位和幅度的起伏，因而更具有确定性。

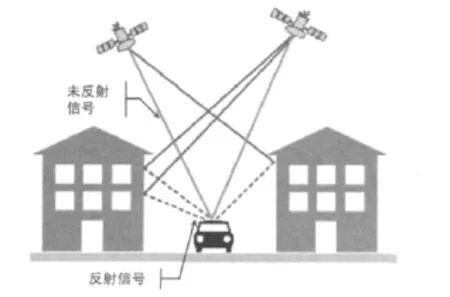
图1 多径原理图

1.2 多径对信号接收处理的影响

接收机在多径环境下的接收信号实际上是直达信号和多径信号的叠加。由于多径信号与直达信号具有相同的信号结构，加之在RF前端存在相同的多普勒偏移，因此，RF前端无法区分直达信号和多径信号，更无法消除多径。所以，多径的抑制一般只能通过天线和信号处理来实现，并且信号处理环节更为重要。

从处理本质上讲，多径主要影响接收机数字处理器中的相关峰计算。多径信号和直达信号具有结构相同但时间不同的伪码，本地信号和多径信号的相关峰不能消除因非正交关系引入的相关边峰，因此，相关函数和鉴别器函数均会受到多径信号的影响，从而进一步影响跟踪精度，引入测距误差。

鉴别器函数的零交叉值表征了用来解算位置的伪距值，任何多径信号都会改变鉴别器函数而使得零交叉值偏移，该偏移量与距离误差相对应。鉴别器函数的一次方程就是早相关峰值减去迟相关峰值，并利用即时相关峰值R（τ）加权。

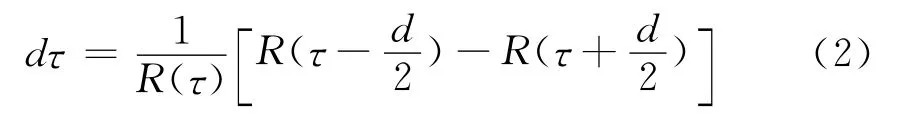
多径效应可以简单地表示为在上述基础上附加第二、第三甚至更多个低幅度的相关峰值。因此，加上或减去多径是可以进行区别的。考虑多径来源和接收机的信号路径，多径误差是以下参数的函数［2]。

信号类型（BPSK，BOC，等等）；信号带宽；码速率；功率电平；由反射引起的信号衰减；多径信号数目；相关间隔及鉴别器类型；载波频率（载波多径）；几何位置；环境参数。

从根本上讲，相关峰越窄受多径影响的概率也就越低。图2示出了多种调制体制的GNSS信号多径误差包络，可以看出多径误差包络是依赖多径延迟的距离误差。与GPS相比，Galileo新信号所具有的窄相关峰能够有效减小多径效应。

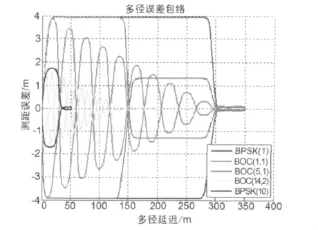
图2 多径误差包络窄相关间隔d＝0.05

由于多径信号传输路径较长，多径信号之间具有相位偏移（在码和载波上有偏移），相位偏移量是几何条件和时间的函数。多径可以同时影响码测量和相位测量，但码片宽度相对较长，码测量的多径误差在数值上比较高。以GPS L1C／A码信号为例，表1给出了码和相位测量的多径误差比较［1]。

表1 GPS L1C／A的码及载波多径比较［1]

多径信号和直达信号根据相位的偏移量可分为建设性（加）叠加和毁坏性（减）叠加，其功率会随时间而变化，进而可以推导得知信噪比会随多径信号数及其相对相位偏移而变化。

此外，只要信号被反射，就可能改变信号的极化方式［3]。依据Brewster角，信号从右旋极化到左旋极化改变，或围绕偶数个反射信号的其他方式改变。GNSS信号是右旋极化信号，因而使用只对右旋极化信号敏感而忽略左旋极化信号的天线可以消除大量反射信号。

1.3 车载GNSS接收机多径的特点

不受多径误差影响的接收机通常只有在广阔的乡间区域才可能实现，自然建筑、山脉、丘陵、溪谷、城市、峡谷，甚至树木和石头都可能导致多径。对于车载应用而言，GNSS接收机的多径条件会不断连续变化而变得更加复杂，多径问题也因此成为市区环境下导航系统最令人烦忧的问题。作为极端多径干扰的例子，必须提到市区场景，在这种场景下，除了自然物体导致的多径外，人造物体也会导致多径，像桥梁、隧道、房屋、交通标志、立交桥和灯柱，甚至也会受到周围车辆以及车辆本身结构的影响。

此外，空间的GNSS卫星会连续不断地改变位置，车载接收机的位置也经常改变，所以多径同时是时间和位置的函数。在静态环境应用中，通过重现卫星星座能够确定多径，但是在动态环境下是不可能的。周边环境的精确模型在原理上可以帮助估计多径环境或建立多径环境模型，而这些模型对于车载应用而言是不可用的，对于具有低处理功率要求的GNSS接收机，所需要处理的数据量太大。

总之，车载GNSS接收机的多径具有复杂、多变的特点，很难进行常规估计。此外，车载应用中不仅需要考虑一个信号的影响，还需要考虑来自所有卫星所有信号的多径影响，并且所有信号的多径干扰程度也是不同的。

2 可用多径抑制方法及分析比较

多径抑制方法可分为天线技术、信号处理和导航解算三类，也有人将基于信号处理和导航解算的多径抑制方法进一步分为直接缓解技术和估计技术两类。

2.1 基于天线的多径抑制方法

天线是导航信号接收处理的最前端，直达信号通过天线进入GNSS接收机的同时，多径和干扰信号也同样进入接收机。为了正确地接收直达信号，尽可能早地去除干扰至关重要，可以根据直达信号的波形特征针对性设计适合接收该类信号的天线。

1）改进的单体天线

GNSS信号是右旋圆极化信号，在镜面反射情况下，极化方式从右旋圆极化变化成左旋圆极化，接收机天线很容易削弱或忽略所有的左旋圆极化信号，但左旋圆极化信号再次反射就成为右旋圆极化信号，可被天线无削减地接收。由建筑、山体和其他环境物体产生的多径信号通常会使低仰角卫星信号降级，对天线采取技术手段使之忽略所有的低仰角卫星信号。一种可行的方法是使用专门的可吸收水平投影的阻塞环天线。阻塞环天线包括很多围绕中心天线的传导同心圆筒，因其结构精密，通常会在外部使用用于保护的盖子。而天线成本、重量和高度是限制天线批量生产的重要因素，应当予以考虑。

2）自适应天线阵列

使用阵列天线是另一个基于天线抗多径的更好方法。阵列天线在任何可能方向形成天线增益波束，这在动态环境中尤为重要。

静态阵列天线包括一组天线阵元和延迟单元，其中延迟单元使每个天线信号的相位产生偏移，所有具有相位偏移的天线信号重叠形成天线波束。自适应阵列天线（也成为相控阵）用于引导增益波束指向明确的卫星，比静态阵列天线更容易使可能的干扰和多径源产生零陷。而车载应用中多径环境连续改变，所以，波束增益也需要相应地快速调整。因为，只有波束方向上的信号能够很好地接收，对于卫星跟踪来说，窄波束最好。但必须提到的是，有必要考虑每个接收信道的自适应信号处理和期望卫星的位置来控制波束。然而，出于大小、重量、能量消耗和成本的原因，自适应天线阵列并不适合车载应用。

2.2 基于信号处理的多径抑制方法

基于信号处理的多径抑制方法是目前研究最为深入和有效的方法。原则上存在两种不同的减弱多径的信号处理方法，第一种是使用单独的相关器技术，通过某种方式分析相关结果去除多径影响，实际的多径信道并不重要，只是用来假定所利用的多径参数，如延迟和衰减。第二种方法是估计多径信道传输函数，通过试图估计多径影响程度，消除多径和干扰对直达信号的影响。此外，近年来还出现了用于多径抑制的频域技术和Ray Tracing技术。

1）相关器技术

信号处理中超过1chip延迟的相关峰可以被忽略，因此，需要判断不同的相关能量，以避免将干扰信号相关峰作为直达信号相关峰。抗多径技术的实现需要充分结合信号／接收机进行调整和优化，不同技术的应用需要综合考虑。例如Galileo系统对BOC调制方式的应用使信号体制自身的多径抑制能力得到了增强。

应用于快速动态变化车载环境的多径抑制相关器技术有多种，如窄相关、双Δ相关器、Earlylate斜率（ELS）技术、Early1－early2跟踪器等。仿真表明：在BPSK和BOC调制信号的处理中，这些相关器技术的性能都比相关器间隔d＝1chip的标准超前减滞后鉴别器优越。图3和图4示出了针对这两种调制信号不同相关器的仿真结果。

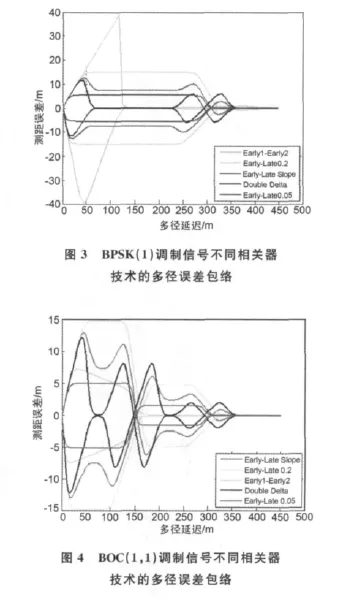
根据仿真结果可知，对于BPSK（1）调制信号，Early1－Early2鉴别器对于减小短延时多径是性能最差，但对于较大多径具有抑制作用。Early－Late斜率技术和窄超前减滞后鉴别器相似，双Δ鉴别器技术性能最好，对于短延时和长延时多径存在距离误差，而对于其他区域伪距误差为0.间距d＝0.2的超前减滞后鉴别器对BOC（1，1）调制信号的多径消除效果最差。Early－Late Slope技术具有相似的伪距误差性能，窄超前减滞后鉴别器技术具有很好的性能。超前减滞后鉴别器在减小相关器间隔时表现出较小的距离误差，但无限小间隔不可能实现。双Δ鉴别器技术对BPSK（1）信号具有很好的效果，但对BOC（1，1）信号消除多径的性能较差，其伪距误差振荡幅度高于间隔为d＝0.1窄超前减滞后鉴别器技术。Early1－Early2鉴别器技术对于减少BOC（1，1）信号多径影响是最好的方法。

对两种不同类型的信号，一种信号相关器技术最好，而另外一种却是最差的。因此，处理两种类型信号的鉴别器最好使用窄超前减滞后鉴别器技术，该方法对两种信号均不是最好也不是最坏。

2）估计技术

估计技术可以用来修正多径误差。多径误差的估计是一个典型的非线性任务，其参数是多维的。车载应用中的多径估计限制因素均是多径的动态变化，在多径信道变化之前必须足够快地计算出估计值。另一个限制因素是用于估计的相关器的个数，每增加一个相关器就消耗一定的芯片资源，并因此增加成本。

最大似然（ML）方法于1995年首次被提出用于多径抑制［4]，该方法考虑了多个影响相关函数的多径信号，并估计其参数。Lentmaier M提出了一种减小复杂度的方法［5]，该方法将问题分解为一维任务和近似迭代最大似然方法，多径估计DLL（MEDLL）、SAGE算法或vision相关器就是该算法的例子。基于ML的各种其他方法可在其他多个文献中看到，有些方法根据应用要求满足理论的Cramer Rao限。但ML具有复杂度和精度有限的缺点，并且没有考虑所有的反射信号，因此，只限于静态测量或测量时间上静止的天线。

表2将可用的估计技术分为静态和动态两类，这些估计技术都可用来估计动态信道或静态多径效应。

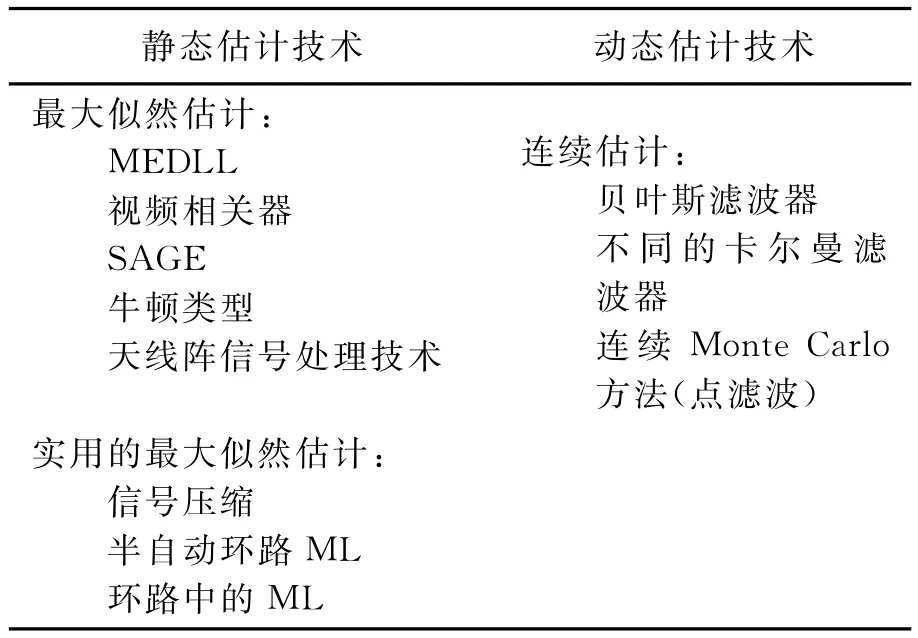
表2 多径估计技术及分类

值得一提的估计技术还有自适应多径抑制滤波器和粒子滤波器方法。自适应多径消除滤波是一种类似于MEDLL的方法，自适应滤波器可以估计多径延迟，用接收信号的相关函数减去多径信号的相关函数，修正的结果反馈到载波和相位鉴别器用于产生载波和伪码。连续蒙特卡洛（SMC）方法是众所周知的粒子滤波器，由于多径传播不是线性过程，所以，卡尔曼滤波不是最佳的多径估计方法，而SMC方法不限于线性模型。

3）频域技术及Ray Tracing技术

频域消除多径的方法类似于时域，即搜索丢失（LOS）信号，在频域意味着查找其频域p0（ω）.除了相位不同于多径信号的反射时间延迟，多径的频域信号非常类似于LOS信号。时域和频域的二值性允许两者之间的互相转换，两个时域信号的卷积与互功率谱的逆傅里叶变换是相同的，互功率谱是相应的两个频域信号乘积，其中一个作为共轭复数。

Ray Tracing技术是一种测定从发射机到接收机的传输路线的算法。该方法基于几何光学，并考虑了反射和折射。为了得到正确的多径估计，需要准确地知道本地环境和目标。车载环境中的Ray Tracing技术需要知道精确定义的环境三维模型。3D城市模型用来提高性能和有效性，但当以50km／h的速度开车穿过城市时，计算量十分庞大。然而，该技术将是一个在未来可用的技术，那时3D模型变得更加成熟，并且芯片的处理性能提高，在加权初始化例程情况下，Ray Tracing可以和码伪距平滑处理相结合。

2.3 基于导航解算的多径抑制方法

基于导航解算的方法用于在观测量的后端处理消除多径影响，并利用受到多径影响的伪距和相位测量值来进行位置求解。基于导航解算的方法包括加权、码伪距平滑、多频率测量、多径衰落信道模型、传感器融合处理等。

1）加权

加权处理即依赖于伪距加权的方法，伪距的处理利用权值矩阵来表示在确定参数时每个观测量的重要程度。可将观测方程表示如下

其中：I为观测值；A为设计（几何）矩阵；X包含未知的参数（至少包括位置和钟差）。参数矩阵可以用以下方式估计

其中，W表示权矩阵，它在确定参数时每个观测量的重要程度，应是选择适当的权值。权值可以由测量的不确定性、卫星的高度、信噪比或者其他的方法确定。受多径影响的信号具有不同的噪声功率，对这些观测量进行权值分离得到更好的位置解。当然，低仰角的卫星信号会显著地受到多径影响，并反映在这些信号的权值分量中。通过调整观测量的冗余度可以更进一步地确定受多径影响比较大的观测量，如RAIM算法，这些观测量被排除在位置求解之外而降低多径影响。

2）码伪距平滑

载波相位测量与伪距测量所受到的影响不同，通过用伪距和相位测量来进行码伪距平滑可以最小化多径的影响。只要没有循环滑动，这个方法具有良好的效果，但循环滑动却是城市环境中汽车应用不可避免的一个问题。利用两个时间点的连续相位测量值，比较它们的多普勒频移与时间间隔的乘积，可以检测到循环滑动。由于观测量权的时间独立性，算法需要几个时间点来得到最好的结果。在循环滑动的情况下，算法会失效，需要用相位测量值来检测是否有循环滑动（用连续时间点的测量和多普勒频移）。出现循环滑动时，权被重置为1，这样会消除循环滑动的影响，以适合车载应用。此外，在测量冗余度高的时候还可以修正循环滑动。

3）多频率测量

多频率测量方法使用信号的联合来估计消除多径信号对一个卫星不同频率不同信号的影响。如果不考虑多径的联合，将会很大程度上涉及到不考虑电离层的联合。GPS将来会提供几个更多的民用信号，像伽利略一样。这些多频信号的发射可以有效地消除多径。

Hill Climbing方法是一种典型的使用多重信号的方法，这种算法采用具有5taps长的自适应信道估计滤波器的预估计器和一种连续的算法。选用BPSK（1）和BPSK（10）两个信号，可以构成典型的GPS系统。在典型的市区环境，这些方法几乎可以消除多径。

4）多径衰落信道模型

卫星信号在传输信道中必定通过受到不同影响的条件才能到达接收机的天线，信道对信号的最大影响是信道损失，并且频率不同、传播环境不同的损失也不同。除了电离层和对流层影响外，其他的影响还包括遮挡，遮挡影响也有一个经验的模型，如用来表示信道损失的COST Hata模型或者Okomura模型。多径和衰落是很小的信道影响。考虑到多径时，时不变信道变为时变信道。时间离散意味着频率选择性，因此，多径信道有一个频率选择衰落效应。频率选择衰减（时间离散）和时间选择衰落（多普勒展宽）可以合并到 WSSUS模型中。也就是说时间变化是广义不变的，不同时延下的衰减和相位偏移是非相关离散的，进而可以用时变系统函数（也称Bello函数）描述。

除了这些标准的多径信道模型，还有其他方法可以表示信道影响的模型。例如室内峡谷中无LOS多径传输模型的射线径迹方法以及德国航天中心（DLR）建立的陆地移动多径信道模型（LMMCM）等。

5）传感器融合处理

传感器融合方法是依赖于GNSS和其他传感器测量值的处理方法，目的是最小化所有的影响GNSS观测值的误差。尽管应用传感器信息的方法可以应用于基于天线和信号处理的多径抑制，目前，传感器融合策略也开始应用于基于导航解算的消除方法中。传感器信息可以用于接收机架构的不同层次，并且其信息需要预处理（如校准）和滤波。利用传感器信息可以简化波束形成、辅助跟踪环、与伪距测量值比较、联合定位滤波器、多源信息融合定位等。

可用于多径消除的传感器包括所有的提供导航相关信息或者各种相关信息的传感器。因此，自动传感器，像加速器、陀螺仪、磁力计、气压计，也包括其 他 的 导 航 系 统，例 如，UWB－positioning，RFID－positioning等。对于汽车应用，可能会有地图匹配一类的传感器来输入到消除多径效应，这在多车道通行应用中会很重要。

3 车载多径消除策略综合考虑

在汽车环境苛刻情况下实现GNSS信号的高效接收是很大的挑战，一方面车载环境的多径变得更加复杂和多变，另一方面，车辆环境的接收机需要实现低能耗。这就意味着需要先进的数字信号处理和软件设计方案，并必须按这个目标设计。所以，计算速度快但价格高的数字信号处理硬件在广泛应用的车载多径消除中是不可取的。

多径信道的变化速度很快，还依赖于卫星的运动，尤其是机动车辆运动引起的环境改变。由于变化速度很快，只有快速实时多径消除技术可以应用。因此，大多数如Ray Tracing、粒子滤波等多径估计技术由于其计算复杂而不太适用。而信号处理方法（如移动相关技术）、基于导航解算的方法（例如加权和码伪距平滑）和传感器融合方法（例如陀螺仪或加速度传感器）成为首选方法。

4 结 论

根据上述分析和比较，综合考虑车载GNSS接收机的特殊应用环境，基于信号处理的方法和导航计算的方法更加适合车载接收机应用。尤其是相关器技术、频域技术、加权及多频测量技术等。传感器融合技术作为车载条件特有的方法也可以充分考虑，并且能够在服务连续性方面带来好处。而基于天线的方法只能在成本允许的前提下有选择的应用。

［1]RAY J R.Mitigation of GPS code and carrier phase multipath effects using a multi－antenna system［D].Department of Geomatics Engineering，University of Calgary，March，2000.

［2]PANY T，IRSIGLER M，EISSFELLER B.Code and carrier phase tracking performance of a future Galileo RTK receiver［C]／／ENC－GNSS 2002，USA：Copenhagen，2002：382－387.

［3]IZADPANAH A.Parameterization of GPS L1multipath using a dual polarized RHCP／LHCP antenna［D].Department of Geomatics Engineering，University of Calgary，2009.

［4]VAN NEE D J R，TOWNSEND B R，FENTON P C，et al.The multipath estimating delay lock loop：Approaching theoretical accuracy limits［C]／／ION GNSS，USA：Palm Springs，Texas，1995：18－20.

［5]LENTMAIER M，KRACH B，ROBERTSON P，et al.Dynamic multipath estimation by sequential Monte Carlo methods［C]／／ION GNSS，USA：Fort Worth Convention Center，Texas，2007：1712－1721.

［6]张孟阳，吕保维，宋文淼.GPS系统中的多径效应分析［J].电子学报，1998，26（3）：10－14.