回归分析和BP神经网络在地表沉降监测中的应用①

陈 帅，朱小玉，王 鹏，姜 楠

（安徽理工大学 测绘学院，安徽 淮南232001）

0 引 言

在地表沉降监测中，准确地对监测点的变形进行预测是非常必要的，随着计算机应用水平的快速提高，现阶段预测沉降的数学模型和方法有许多。为提高数学模型在地表沉降监测及规律预测中的准确性，采用了回归分析法中的曲线拟合法和BP神经网络模型的数值处理方法并进行比较，得到模型适合预测的范围。

1 模型的基本原理

1.1 回归分析法

回归分析法是利用数理统计原理，对大量的统计数据进行数学处理，并确定因变量与自变量之间的相关关系，建立一个相关性较好的回归方程，并加以外推，用于预测因变量的分析方法，是最常用的数理统计方法。通常线性回归分析法是最基本的分析方法，而求一个变量对另一个变量的因果关系，叫一元回归分析。

设以x为自变量，y为因变量，则一元线性回归模型可表示为

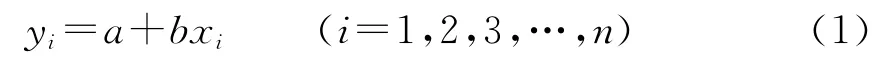
式中：a、b为回归系数；i为观测次数。

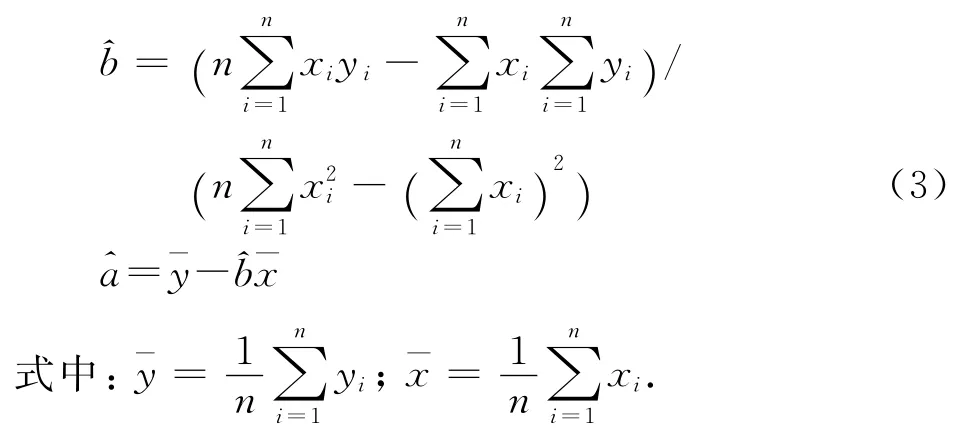
1.2 BP神经网络模型

BP神经网络是一种基于误差反向传播算法的多层前馈网［2]。它是一种由输入层、隐含层和输出层构成的多层向前神经网络，本质是以网络误差之平方和为目标函数，按梯度法求其目标函数达到最小值的算法。其主要特点是：每个激励函数是可微的Sigmoid函数；多层感知器的多个突触使得网络更具连通性，连接域的变化或连接权值的变化都会引起连通性的变化［3]。图1为BP神经网络的拓扑结构。

BP算法的学习过程就是使能量函数最小化的过程，由两部分组成：信息的正向传递与误差的反向传播。在正向传播过程中，输入信息从输入层经隐含层逐层计算传向输出层，每一层神经元的状态只影响下一层神经元的状态。如果在输出层未得到期望的输出，则计算输出层的误差变化值，然后转向反向传播，通过网络将误差信号沿原来的连接通路反传回来修改各层神经元的权值直至达到期望目标［3]。

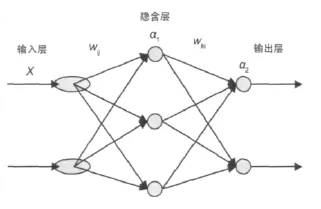
图1 BP神经网络的拓扑结构

假设输入为x，输入神经元有r个，隐含层内有s1个神经元，激活函数为f1，输出层内有s2个神经元，对应的激活函数为f2，输出为a，目标失量为t，则隐含层中第i个神经元的输出为

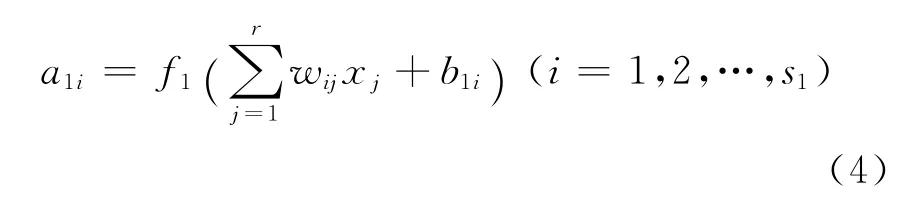
输出层第k个神经元的输出为

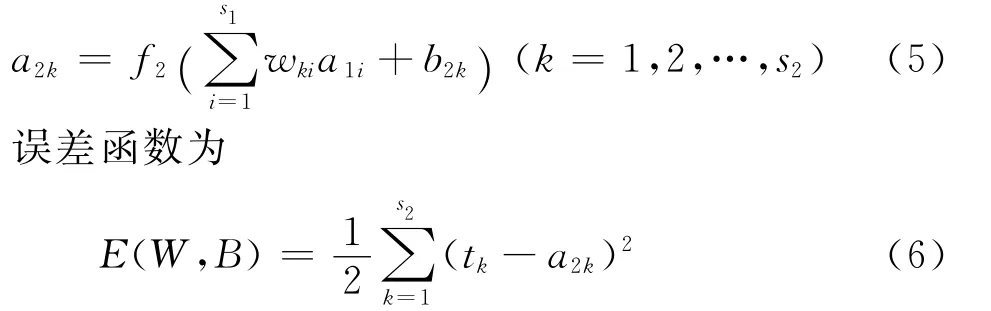
输出层的权值变化为

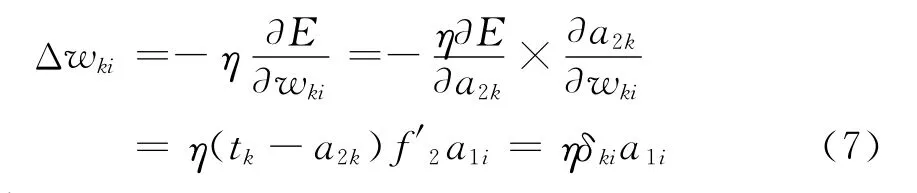
式中：δki＝（tk－a2k）f′2＝ekf′2；ek＝tk－a2k.同理可知

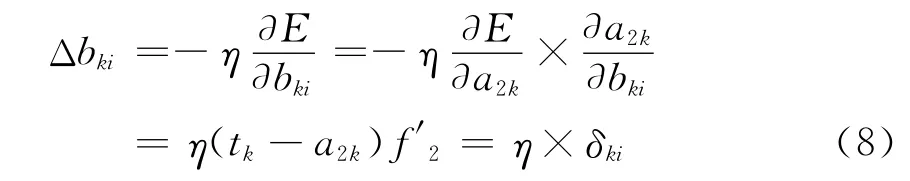
隐含层权值变化为

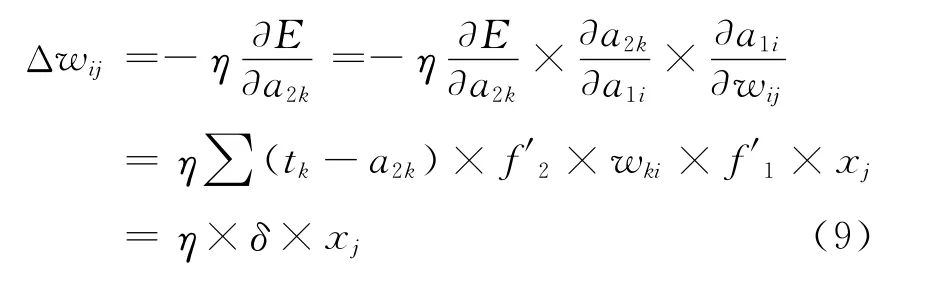
同理可得

Δb1i＝ηδij

对于f1为对数S型激活函数

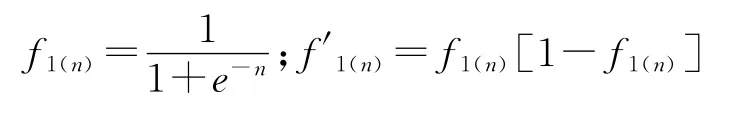
对于f2线性激活函数

f′2（n）＝n′＝1

为加快训练速度，避免陷入局部极小值，可采用附加动量法、变尺度法和变步长法进行BP网络的改进。这里用的是附加动量法。

带有附加动量因子的权值调节公式［5]

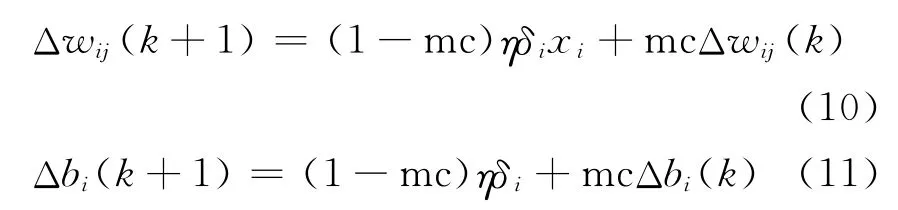
式中：k为训练次数；mc为动量因子，一般取0.95.

2 模型对比

采用某矿区的实测资料，通过建立两种预测模型的数学源程序模型，输入原始数据资料，分别用以上两种模型进行预测训练和测试，得到预测模型，输入预测时间，即可得到具有相当精度的预测量，如表1所示。

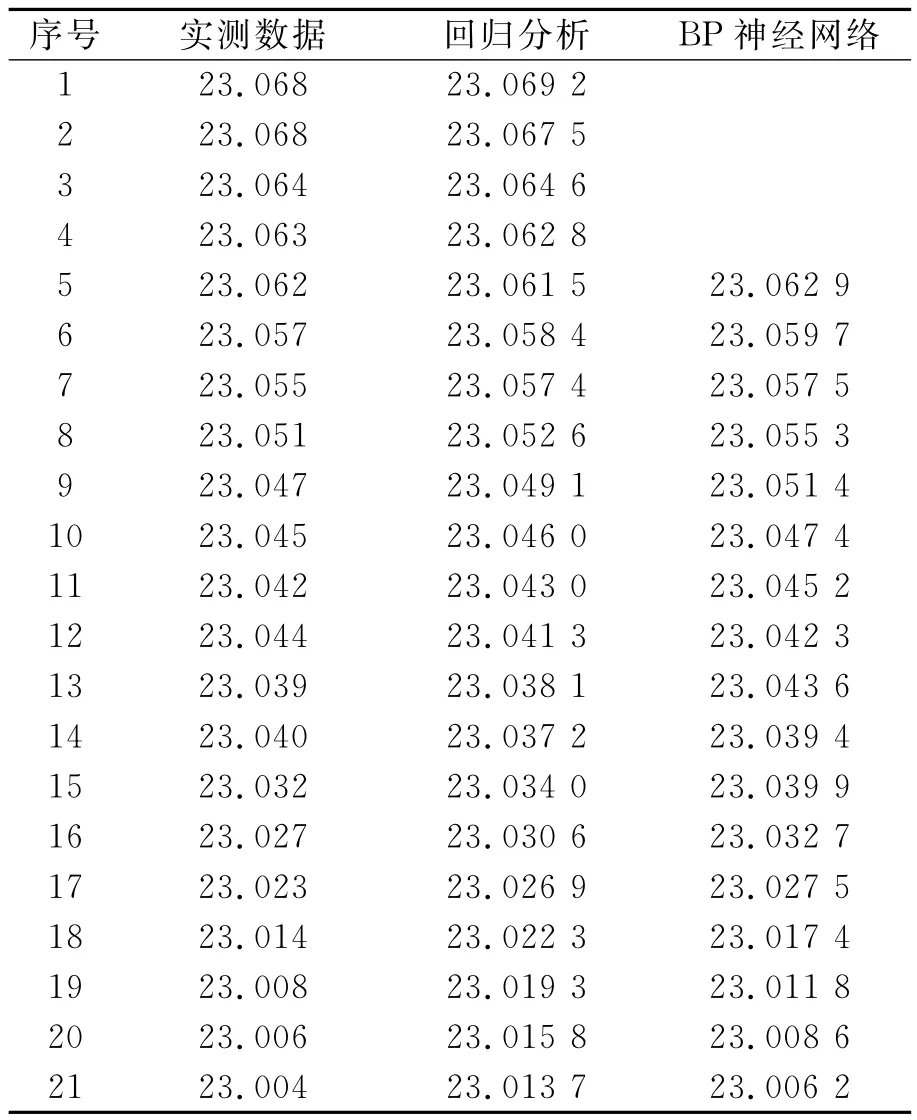
表1 模型在实测点预测结果相比较／m

通过两种预测模型的预测值与实测值比较可以看出，在前期的预测中，采用回归分析和BP神经网络预测的结果和实测值拟合的比较好。后期由于数据的跳跃性，采用BP神经网络预测的结果比回归分析法预测的结果要好，如图2所示。

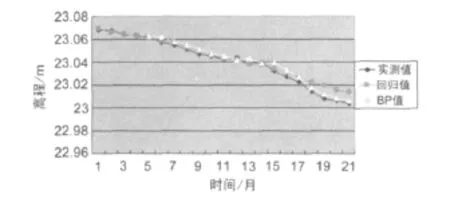
图2 模型预测值比较

3 结 论

通过样本训练和测试，得到了回归分析法中的曲线拟合法和BP神经网络模型在地表沉降预测中各自的有效性和精确性。地表沉降预测是一种快速准确预计地表下沉的方法，选择合适的预测模型进行预测，对提高信息预测的精度和准确度有着积极的意义。

［1]孙 华.一元线性回归模型设计及C＋＋实现［J].长沙医学院学报.2008（12）：47.

［2]MARTIN T H，HOWARD B D，MARK H B.神经网络设计［M].戴 蔡译.北京：机械工业出版社，2002.

［3]高 隽.人工神经网络原理及仿真实例［M].2版.北京：机械工业出版社，2007.

［4]申 哲，葛广英，田存伟.浅析BP神经网络设计中的关键问题［J].科技信息，2011（6）：238－239.

［5]刘启中，施一萍，白彩英.基于BP神经网络的盾构施工变形预测［J].计算机应用与软件，2005（4）：3－5.