阶梯板兰姆波散射特征模式展开法研究
凤飞龙,陈文生
(1.无损检测技术教育部重点实验室(南昌航空大学),南昌330063;2.西安工程大学,西安710048)
0 引言
兰姆波作为导波的一种,是一种经济有效的薄板扫查检测方式。经常被应用于金属板材、复合材料的质量检验与在役检测[1]。考虑到板材内部可能具有不同的缺陷以及在使用环境中不同的腐蚀缺损状况,在实际检测时往往需要对被检测缺陷或者缺损作出特定判断。比如对于金属板材的腐蚀,往往需要设定缺陷模型为阶梯板[2]。虽然不能准确估计缺陷的尺寸,但可以根据回波幅度得到当量尺寸。在现代几种大型商业检测系统[3]尚未普及之前,兰姆波检测的准确性往往基于经验判断。比如,在低频端,兰姆波最低阶对称模式s0模的反射或者透射回波和阶梯板的板厚损失成线性比例。这一设定无疑满足板材检测中的定位与粗略定量要求;但是考虑到兰姆波多模式及频散特性,这些基于部分散射特征的缺陷判断基准使兰姆波的检测在应用范围上受到限制,即要求低频率板厚积(频厚积)。因为在高频厚积应用场合,阶梯板的散射特征更为复杂,缺陷定量难度相应增加;为此,与数值模拟软件相结合的检测分析学习或者对比系统成为目前一些商业检测系统的重要特征。
到目前为止,国内外学者对于阶梯板的兰姆波散射分析基本上基于数值计算方法[4-6]。即有限元、边界元、以及相关的混合有限元或者边界元;但这些方法只能针对十分具体的结构建模分析,比如需要构建某个具体模式在某频率下在某具体厚度的板中传播,相对于确定尺寸缺陷发生散射,然后对散射特征进行分析。如果尺寸、频率改变则需要重新建模,总体上讲,对于分析某一类散射体散射特征而言,需要大量的建模时间;因此,许多学者致力于求解散射场的解析求解方法,用统一的解析公式分析散射体对兰姆波的散射特征。由于求解难度,目前的研究往往只局限于几种,包括板端[7],板中裂纹[8-9],板中圆柱[10],板中材质不均[11],板厚缓变起伏[12]等等。笔者基于文献[13]的工作,给出阶梯板散射的模式展开法求解公式,分析阶梯结构不同尺寸参数对散射的影响规律,拟发现一些新的散射特征。
1 模式分解方法
考虑无限大材料均一等厚板在xoy平面上的截面如图1a所示。对稳态声场,可以将位移与应力场分解成2 个向量[11]:X=(u,t)T和 Y=( -x,v)T。其中u,v是y方向和x方向的位移分量,s= σxx,t= σxy,σ是应力张量。这2个场向量又可以按照下式用兰姆波模式分解:
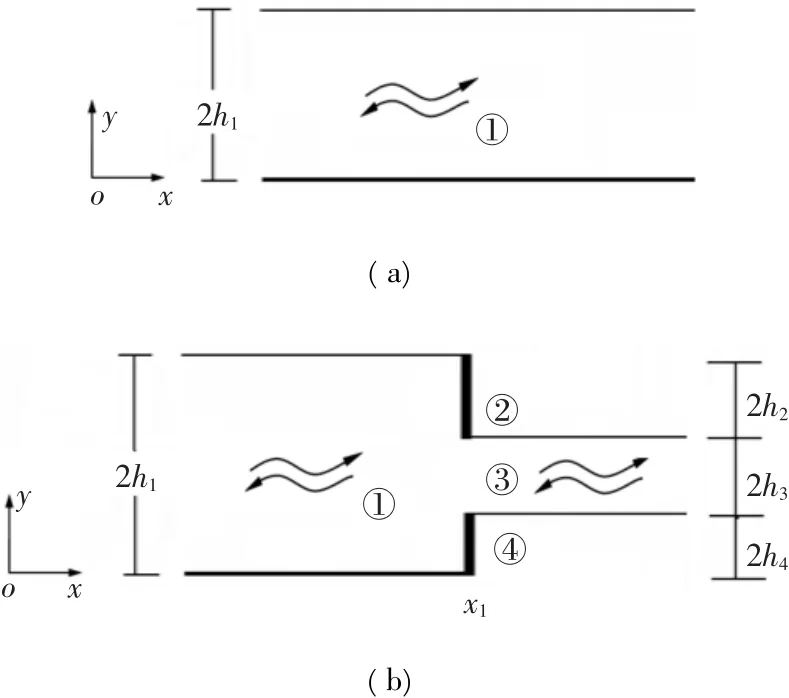
图1 等厚板、阶梯板的结构示意图Fig.1 Schematic graph of equal-thickness plate and step plate

其中:Xn=(Un,Tn)TYn=( - Sn,Vn)T;Un、Vn、Sn、Tn是兰姆波模式的波结构函数,分别对应u、v、s、t。式中的分解系数an和 bn可以用Fraser双正交性关系分解[11]
其中,An(x)和Bn(x)分别是左行和右行兰姆波模式的幅度。所有模式的幅度可以用向量A(x)和B(x)表示。模式分解法的基本思想是利用散射体的边界条件,分解出特定模式入射时各散射模式的幅度信息。这通常用散射矩阵来描述。对图1b所示的阶梯板,根据x1处板的位移和应力连续条件,可以得到

由式(1)~式(3)可以进行模式分解得到的散射矩阵如下

其中各分块矩阵都可以得到解析计算公式,具体形式如下,推导过程参见文献[13]。
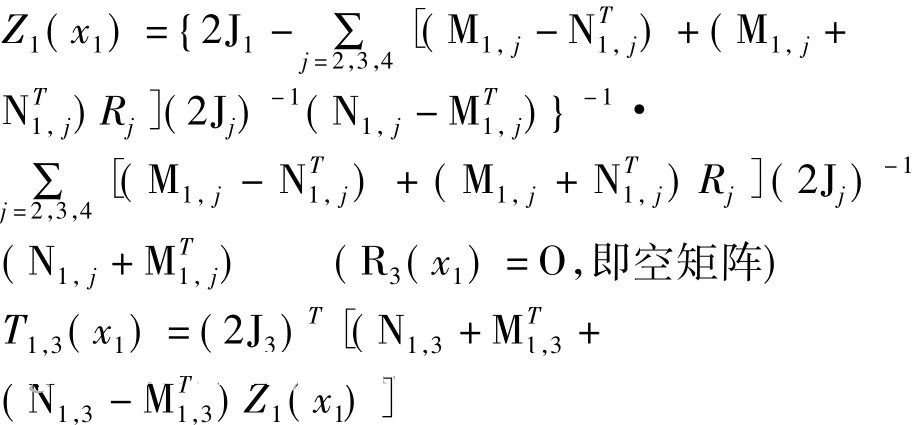

采用以上公式编写程序,只需给定兰姆波频率和阶梯尺寸,就可以求解任意传播模入射时的散射系数;因而,计算效率较数值方法高很多。
2 阶梯板的散射特征分析
2.1 上下对称阶梯板厚度比对散射的影响
参照图1b,设阶梯结构沿板中性面对称,并且板①与板③厚度分别为2h1=4 mm,2h3=0~4 mm。那么板面上左右两端入射的首阶对称和反对称模式自身的反射和透射系数如图2所示。由于结构对称性,对称模式与反对称模式之间没有模式转换发生。此外,从中可以发现:
1)在频率低于800 kHz时,a0和s0模式透射系数(Ta0(1)a0(3),Ts0(1)s0(3),Ta0(3)a0(1),Ts0(3)s0(1),其中“T”表示透射。Ta0(1)s0(3)表示板①中的a0模式入射时向板③中的s0模式的透射系数。其他依次类推)随阶梯厚度差减小而增大;反射系数(Ra0(1)a0(1),Rs0(1)s0(1),Ra0(3)a0(3),Rs0(3)s0(3),其中“R”表示反射。Ra0(1)a0(1)表示板①内a0模自身的反射系数,其他依次类推。)随阶梯厚度差减小而减少。这种单调线性关系存在于厚端a1模截止频率(对于本例中的钢板,略高于400 kHz)以下;因此,在这个频率以下可以采用自发自收或者一发一收的探头布置,激励并提取a0或者s0模的幅度信息,判断阶梯板厚度差大小。
2)对比100 kHz和400 kHz时的a0模式的散射系数(Ta0a0,Ra0a0)变化曲线,可以发现:板③厚度和板①厚度相差1 mm的范围内,散射系数对于板厚变化不是很敏感;也就是说在400 kHz以下,这个范围内的板厚变化不能有效反映到a0模的透射信号或者反射信号幅度上。板③厚度在1~3 mm之间,高频(400 kHz相对于100 kHz)a0模的反射或者透射信号幅度变化可以有效地对应板厚变化。与之相比,s0模式的透射和反射系数在100 kHz和400 kHz时并无显著变化,高频的散射系数甚至没有低频的散射系数对于板厚变化敏感。说明在低频(低于a1模截止频率)检测对称阶梯板时用较高频率的a0模式可以略微提高对于微小板厚变化的检出率,而用s0模式时,提高频率对于提高微小板厚变化检出率并没有多少改善。
3)在计算频率范围内,阶梯两边的模式之间,对换入射方向,透射系数相等。如Ta0(1)a0(3)与Ta0(3)a0(1)以及 Ts0(1)s0(3)与 Ts0(3)s0(1)。也就是说一发一收提取某模式幅度信息检查厚度变化时,如果只考虑声场能量转化关系,两侧探头可以收发互换。这种现象是兰姆波声场互易性的一种体现。在a1模截止频率以下,两边s0或者a0模式自身的反射系数,如Ra0(1)a0(1)与Ra0(3)a0(3)以及Rs0(1)s0(1)与Rs0(3)s0(3)也相等。这意味着在低于a1模截止频率时从板的两侧收发a0得到的反射信号幅度相同,收发s0模式得到的反射信号也相同。
2.2 阶梯板共底面时厚度比对散射的影响
参照图1b,如果其中2h4=0,那么阶梯两端共底面。板厚为2h1=4 mm,2h3=0~4 mm。a0模式和s0模式在低频时(低于a1模截止频率)散射规律如图3。由于结构不对称,所以对称模式s0与反对称模式a0之间有了模式转换。例如Ta0(1)s0(3)和Ra0(1)s0(1),前者表示从板①入射的a0模透射到板③中转换为s0模的能量比例或者能量散射系数,后者表示板①内入射到阶梯上的a0模式向板①内s0模式的能量散射系数。此外,还可以发现:
1)透射系数 Ts0(3)s0(1)、Ta0(1)a0(3)、Ta0(3)a0(1)越大,反射系数Ra0(1)a0(1)、Ra0(3)a0(3)、Rs0(3)s0(3)、Rs0(1)s0(1)越小。这与对称阶梯板的散射规律相似;而透射和反射中的对称与反对称模式转换系数随阶梯差变化具有抛物线特征。
2)无论s0模式还是a0模式,频率越高,越接近a1模截止频率,散射系数 Rs0(1)s0(1)、Ts0(1)s0(3)、Ra0(1)a0(1)、Ta0(1)a0(3)、Ra0(3)a0(3)、Rs0(3)s0(3)对于阶梯板厚差的细微变化越敏感,尤其是在接近a1模截止频率时最显著。这与对称阶梯板的情形不同。另外频率越高,对称反对称模式转换现象越显著。
3)与对称阶梯板相似,阶梯两端任意两个模式之间的能量透射系数相等,或者说呈现一种互易性。如Ts0(3)a0(1)(板③中s0模入射时对板①中a0模的透射系数,其它依次类推)与Ta0(1)s0(3),Ts0(1)s0(3)与Ts0(3)s0(1)等等。但是阶梯两边的a0与s0模式自身的反射系数却不相同,即Ra0(1)a0(1)与 Ra0(3)Ra0(3)不等,Rs0(1)s0(1)与Rs0(3)s0(3)不等。这意味着从两侧检测板厚变化时,遵循的回波信号幅度与板厚变化多少的对应关系不同。这与对称阶梯板不同。

图2 轴对称阶梯钢板散射规律,板厚:2h1=4 mm,2h3=0~4 mm,蓝绿红浅蓝分别对应100 kHz,400 kHz,800 kHz,1.2 MHzFig.2 Scattering characteristics of Lamb wave at symmetric step-like thickness variation:2h1=4 mm,2h3=0 ~4 mm Harmonic frequency:100 kHz(blue),400 kHz(green),800 kHz(red),1.2 MHz(cyan)
2.3 确定厚度比时阶梯相对位置对散射的影响
参照图1b如果2h3=2 mm,2h1=4 mm,改变2h2=0~2 mm,2h4=2~0 mm,那么 a0模与 s0模的散射系数变化曲线如图4所示。从图中可以评判不同模式散射系数对于板厚改变对称性(板①与板③的厚度差一定的情况下,两者中性面接近的程度,2h2=1 mm时两者共中性面,意味着板厚对称改变)的敏感程度:
1)能量散射系数曲线全部以2h2=1 mm为中心,对称分布。仅从能量散射系数不能判定板两侧哪一侧厚度损失或者增加更多。
2)沿入射方向,如果板厚增厚,即入射方向是从板③到板①。随着板厚变化对称程度增加,除了a0模式反射系数Ra0(3)a0(3)减少外,s0模与a0模的反射和透射系数(Ta0(3)a0(1),Rs0(3)s0(3),Ts0(3)s0(1))都增加。沿入射方向,如果板厚减薄,随着板厚变化对称性增加,除了s0模式的反射系数(Rs0(1)s0(1))减少外,s0模与a0模的反射和透射系数(Ta0(1)a0(3),Ra0(1)a0(1),Ts0(1)s0(3))都增加。
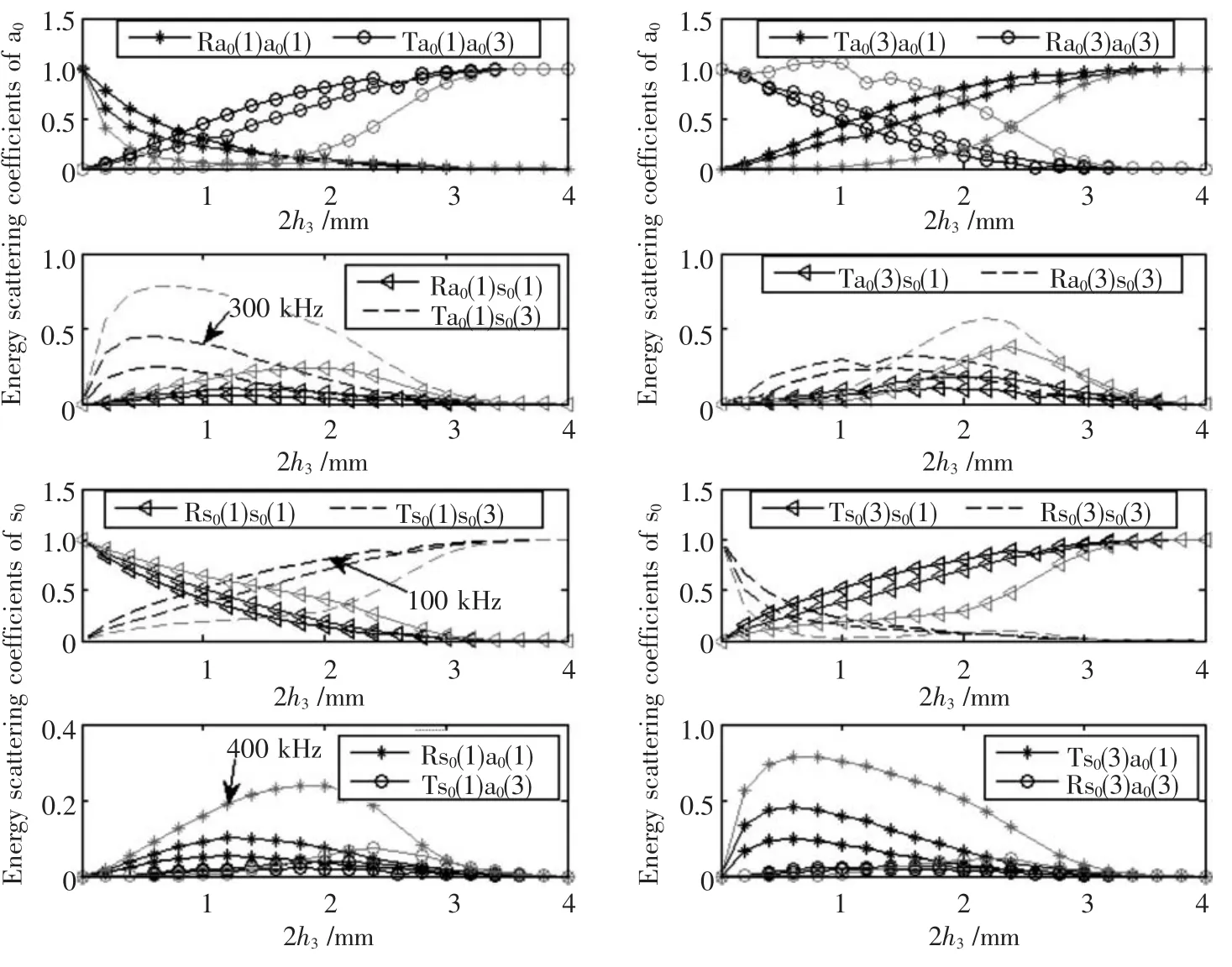
图3 共面阶梯钢板散射规律,板厚:2h1=4 mm,2h3=0~4 mm蓝红浅蓝分别对应100 kHz,400 kHz,800 kHzFig.3 Scattering characteristics of Lamb wave at step-like thickness variation on one surface:2h1=4 mm,2h3=0 ~4 mm Harmonic frequency:100 kHz(blue),300 kHz(red),400 kHz(cyan)
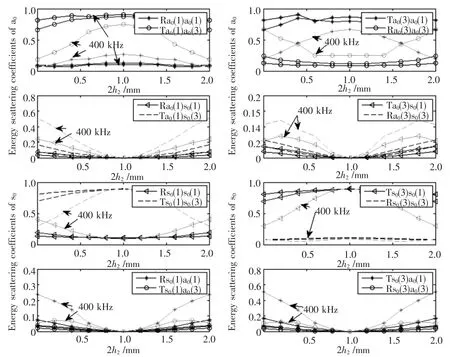
图4 对称性对阶梯板散射的影响,板厚:2h1=4 mm,2h3=2 mm,2h2=0~2 mm,蓝红浅蓝分别对应100、400、800 kHzFig.4 Effect of structure symmetry on scattering coefficients,where 2h1=4 mm,2h3=2 mm and 2h2=0 ~2 mm Harmonic frequency:100 kHz(blue),300 kHz(red),400 kHz(cyan)
3)无论沿哪个方向入射,对称模式与反对称模式之间的模式转换系数,反射(Rs0a0,Ra0s0)系数和透射(Ta0s0,Ts0a0)系数均减小。
4)频率增加,以上现象对于阶梯厚度变化对称性的敏感程度增加。
5)两个入射方向上透射系数具有互易性,即从散射区左侧模式A入射到散射区右侧模式B的能量比例,或者从散射区右侧模式B入射到散射区左侧模式A的能量比例,两者相同。A与B可以是相同模式。
3 结论
以上计算验证了一些已有的阶梯板散射规律:板内s0模式或者a0模式入射波遇到不对称厚度改变时,有模式转换现象;s0模式与a0模式的反射系数并不总是随厚度差增加而单调增加,只有频厚积较小时才呈现这样的规律。
此外,通过计算发现:
1)以往认为频率增加,兰姆波对于小尺寸厚度变化的检测能力增加。在不对称厚度变化的情况下,该假定成立;如果板厚度变化对称,而入射模式为s0模式,该假定并不成立。
2)阶梯板任意两侧传播模式之间的透射系数具有能量上的互易性。如果阶梯板对称,在低频时(低于a1模截止频率),a0、s0模在散射区两侧的反射系数相等。
3)在低频下,若板厚变化趋近于对称,a0、s0模式自身的透射系数都增加,相互之间的模式转换减少。
根据这些结果,可以认为,检测板厚变化时,a0模比s0模具有更好的适用性;在a1模截止频率以下提高a0模的检测频率能提高对于小厚度变化的检出率;一发一收法检测时,收发互换,若两探头输入输出阻抗性能一致,接收到的信号幅度相同;除非阶梯板对称,单发单收法检测时探头置于散射区两侧回波幅度不同;低频时模式转换能量减少意味着入射模式透射能量增加。
[1]Rose J.A baseline and vision of ultrasonic guided wave inspection potential[J].ASME Journal of Pressure Vessel Technology-Special Issue on Nondestructive Characterization of Structural Materials,2002,124(3):273 -282.
[2]Cho Y.Estimation of ultrasonic guided wave mode conversion in a plate with thickness variation[J].IEEE Ultrasonics,Ferroelectrics,and Frequency Control Society,2000,47(3):591 -603.
[3]Lowe M,Cawley P.Long range guided wave inspection usagecurrent commercial capabilities and research directions(Internal Report) [DB/OL].www3.imperial.ac.uk/pls/portallive/docs/1/55745699.PDF,2006-3-29/2011-9-8.
[4]Song W,Rose I,Galan J,et al.Ultrasonic guided wave scattering in a plate overlap[J].IEEE Ultrasonics,Ferroelectrics,and Frequency Control Society,2005,52(5):892 -903.
[5]景永刚,张海燕,刘镇清.板材厚度变化对Lamb波透射系数的影响[J].声学技术,2006,25(1):26-29.
[6]田光春,刘镇清,景永刚.台阶型厚度变换板中的导波的研究[J].无损检测,2003,25(7):333-348.
[7]Zhang S,Shen J,Ying C.The reflection of the Lamb wave by a free plate edge:Visualization and theory[J].Material Evaluation,1988,46:638 -641.
[8]Shkerdin G,Glorieux C.Lamb mode conversion in a plate with a delamination[J].Journal of Acoustical Society of America,2004,116(4):2089-2100.
[9]Castaings M,Clezio E,Hosten B.Modal decomposition method for modeling the interaction of Lamb waves with cracks[J].Journal of Acoustical Society of America,2002,112(6):2567 -2582.
[10]Wang M,Ying C F.Scattering of Lamb waves by a circular cylinder[J].Journal of Acoustical Society of America,2001,110(4):1752–1763.
[11]Pagneux V,Maurel A.Lamb wave propagation in inhomogeneous elastic waveguides[J].Proceedings of the Royal Society A,2002,458:1913–1930.
[12]Pagneux V,Maurel A.Lamb wave propagation in elastic waveguides with variable thickness[J].Proceedings of the Royal Society A,2006,462:1315 -1339.
[13]凤飞龙.复杂结构兰姆波散射的模式展开法研究[D].北京:中国科学院研究生院博士学位论文,2007:23-39.

