高频数据下基于组合预测思想的统计套利策略创新设计与实证研究

杨怀东 潘 珺

一、前 言

市场中性策略是一种通过构建避免某类风险暴露的多空头寸组合规避市场风险，并利用头寸间相对价格变化来获取绝对收益的投资策略。头寸组合的多头和空头需要严格匹配，收益水平取决于交易时机与配对组合的选择能力，而非源于市场走势。统计套利通过建立时间序列模型拟合资产价格变化规律，识别资产组合内部统计错误定价关系，寻找两个或者两个以上资产间存在的套利机会，再进一步设定交易阈值，并通过计算机自动发出交易信号执行投资过程，是一种基于统计模型挖掘套利机会的中短期市场中性投资策略。

统计套利策略的技术关键在于构建能发现更多、更普遍及更持续套利机会的统计模型以及交易规则的选择，近期相关研究多集中于此。Bolgun等（2009）对伊斯坦布尔股票交易所ISE30指数成分股日收盘价进行动态统计套利实证结果表明，成对股票组合产生的日平均收益率相对于单纯的购买并持有策略高3.36%，但交易限制和交易佣金却消耗了大部分超额收益率。Low（2009）的实证表明，牛市中股票市场中性策略并不能完全获得市场收益率，但在熊市中却能完全避免市场下跌的风险，获得稳定低风险收益率。Bertram（2009）推导出证券价格服从伊藤扩散过程时基于预期收益率最大化条件下的最优统计套利策略解析式，并运用一只在澳大利亚和新西兰股票交易所同时上市的银行股进行了实证检验。

国内研究尚处起步阶段，研究内容主要集中在局部理论问题与套利策略实证分析。方昊（2005）认为统计套利对象在经济意义上应具有一定的趋同性，具有相当好的流动性，最后价格比序列也必须是平稳的，并将统计套利模型应用在封闭式基金市场，结果表明统计套利策略是有效的。韩广哲等（2007）运用方差比分析法将统计套利运用于上证50指数成分股之间的套利，考虑了三种交易成本及费用水平对统计套利策略绩效的影响，实证结果表明统计套利策略是有效的，但在样本外的绩效对交易成本相当敏感。常宗琪（2008）基于协整模型并采用日内收盘数据，对郑州期货交易所的白糖期货合约的跨期套利机会进行实证检验。研究中将交易进场点为1σ，出场点为2σ，止损点为0.9σ，并进行了简单演示，并提出可采用日内小时数据来进行统计套利研究。仇中群等（2008）基于协整模型并采用IF0806与IT0807合约的一分钟高频数据，对沪深300股指期货模拟交易进行分析。由交易时机图发现，价差序列长时间处于无套利带外，并一直没有回归到均值附近，说明股指期货仿真交易市场存在一定的跨期套利空间，统计套利策略是有效的。徐光梅（2008）同样采用协整模型对浦发银行和招商银行统进行成对交易的实证研究，运用GARCH模型来估计时变标准差，用于交易触发点的设置，并根据固定交易触发点与时变交易触发点将统计套利策略分成两种策略，实证表明采用时变交易触发点的策略绩效更高。刘华（2008）采用协整模型并基于日数据将统计套利策略中的成对交易运用在上证50ETF与沪深300股指期货的期现套利上，实证研究表明，统计套利策略在样本内外均取得了较好的效果，其受市场的影响较小，在各个市场环境中均获得了比较稳定的收益。

可见，协整模型是国内外统计套利策略的传统基础模型，但协整模型估计参数是不变的，而这与金融序列模型参数的时变性是不相符的。张波（2008）将卡尔曼滤波用于投资决策以估计投资收益，文献则将其运用于估计期货价格期限结构，均取得了较好的效果。其次，由于市场环境是不断变化的，模型应用于统计套利策略的效果通常也是时变的。组合预测是综合各种预测方法以提高整体预测精度的方法，文献将其运用于预测石油价格、我国的GDP、我国股票市场波动率，均取得了很好的效果，但目前尚无文献将组合预测思想引入到统计套策略中。此外，采用日数据是传统统计套利的惯例，但对于高频数据下的统计套利策略的有效性、配对股票选取及数据频率对套利绩效影响等诸多问题，尚缺少实证分析。

本文选取日数据和5种日内高频数据，引入估计时变参数的理想模型——卡尔曼滤波模型，并进一步借鉴引入组合预测思想，综合利用传统协整模型和新引入的卡尔曼滤波模型，与统计套利策略的具体目标相结合，设计新的组合策略以提高统计套利策略的整体绩效，实证分析数据频率、策略选择对我国股票市场的统计套利机会及其收益性的影响。

二、基于组合预测思想的统计套利策略创新设计

组合预测是综合利用各种模型，从而提高整体预测精度。基于这种思想，本文综合利用协整套利模型及考虑到金融序列参数时变性而引入的卡尔曼滤波模型，结合具体目标对统计套利方案进行设计。

（一）协整模型与卡尔曼滤波模型

（1）协整模型

对价格时间序列协整分析最常用的是恩格尔协整分析两步法。首先进行OLS回归分析，运用样本内数据估计建立的回归方程：P1t=β×P2t+μt，其中P1t和P2t分别表示两只具有相关性的股票在t时刻的前复权收盘价，μt为随机扰动项。然后对回归方程的残差序列进行ADF单位根检验。

（2）卡尔曼滤波模型

在传统协整分析中，假定参数β是固定不变的，而金融时间序列模型参数通常是具有时变性的，因此将估计时变参数的理想模型--卡尔曼滤波模型引入到统计套利策略中，用于描述资产价格关系。运用样本内数据估计建立的量测方程和状态方程：

量测方程：P1t=βt×P2t+μt

状态方程：βt=βt-1+θt

其中，μt和θt是两个相互独立的随机误差项。

（3）价差序列的去中心化处理

采用协整模型和卡尔曼滤波模型得到相应的价差序列Spread，分别求出两模型下相应的价差长期均值和标准差，然后进行去中心化处理，得到Mspread序列。

（二）基于协整模型及卡尔曼滤波模型的统计套利策略交易信号发出规则

（1）进场点：

当Mspread＞0时，说明回归方程左边的股票相对于右边的股票高估了，而当Mspread大到一定程度时，可以覆盖双边交易成本时，便可以卖出方程左边的高估股票，买入方程右边的低估股票，当Mspread回归到0时便将两只股票分别平仓获得利润。

当Mspread＜0时，说明回归方程左边的股票相对于右边的股票低估了，而当Mspread小到一定程度时，可以覆盖双边交易成本时，便可以买入方程左边的低估股票，卖出右边的低估股票，当Mspread回归到0时便将两只股票分别平仓获得利润。

根据我们的前期研究成果，见文献，设置较高的交易触发点是运用高频数据进行套利时提高收益率的一个有效途径，因此本文在样本内外均将采取单次收益率最大化作为进场条件，根据价差的正态分布假设，在95%的置信水平下，价差偏离其长期均值的可能性不会超过1.96倍标准差，因此2σ已是价差偏离其长期均值的最大程度，因此将2σ设置为进场点。由于价差偏离其长期均值的程度处在极限情况下，更有回归均值的需求，其回复速度也更快，类似于技术分析中的超买超卖现象。

（2）出场点

止损点则采用3σ这个更高的安全界限，同时，为提高收益的实现率，将回复均值的条件放宽为价差偏离长期均值的程度小于或者等于0.5σ。

（三）基于组合预测的统计套利策略规则

（1）进场信号

由于单次收益率最大化策略的进场点设置得比较高，因而交易机会相对较少，基于此，考虑到协整模型和卡尔曼滤波模型效果的时变性，因此只要有一个模型发出进场信号，则进场交易，增加交易机会。

（2）平仓信号

当一段时间内，只有一个模型发出了进场信号和平仓信号，则根据该模型发出的信号进行平仓，以增加收益的实现率。

当一段时间内，协整模型和卡尔曼滤波模型均发出了进场信号和平仓信号，则按较晚发出平仓信号的模型信号进行平仓，以扩大收益率（由于平仓点设置为0.5σ，延长平仓时间，有可能使平仓点更接近均衡点，而使收益率扩大）。

（3）止损信号

当一段时间内，只有一个模型发出了进场信号和止损信号，则根据该模型发出的信号进行止损，防止价差不向均值回归而造成损失。

当一段时间内，协整模型和卡尔曼滤波模型均发出了进场信号和止损信号，则按较晚发出止损信号的模型信号进行止损，即当两个模型都已经发出止损信号则进行止损，以避免过早止损而造成收益无法实现。

当t-1日（时刻）止损出场，且t时只有一个模型发出进场信号时，则不进场，避免过早进场造成损失。直至两个模型都已发出进场信号，则进场交易，以提高进场信号的正确率，从而提高收益的实现率。

三、实证研究

（一）数据来源及处理

数据来源及处理见文献，统计套利数据选取见表1，并根据该文中我们所取得的前期研究成果，选取同属煤炭采选业的中国神华与中煤能源作为研究对象。

（二）交易成本及费用说明

机构投资者通常可以享受0.03%的优惠佣金率，单边单只股票的佣金率为0.03%，印花税率单边卖出单只股票0.1%，则完成一次套利所需交易成本为0.32%，再考虑0.1%的流动性成本，则总成本为0.42%。此外，还需考虑融券费用，大多券商的融券费率为9.86%一年，则每天的融券费率为0.027%，按实际使用天数计算。本文研究中，由于运用日数据和60分钟数据单次套利持续时间较长，因此融券费率按实际天数计算，而运用30分钟、15分钟数据进行单次套利的持续时间短，运用5分钟及1分钟进行套利则由于同日操作较多而单次套利可能涉及两只股票的融券，所以这4个频率的单次统计套利的融券费率简化计算为0.05%。

表1 统计套利数据选取

因此，运用日数据和60分钟数据进行统计的单次成本与费用为0.42%再加实际融券费用，而运用30分钟、15分钟、5分钟及1分钟数据进行统计套利的单次成本与融券费用和为0.47%。

（三）基于协整模型及卡尔曼滤波模型的统计套

利策略交易信号发出的具体规则

（1）基于协整模型的统计套利策略交易信号发出的具体规则

通过对各频率样本内数据进行ADF单位根检验发现，12个原价格序列在3个置信水平下均未通过平稳性检验，但在1%的置信水平下，12个价格一阶差分序列则均通过了检验，说明在1%的置信水平下，12个价格序列均为一阶单整序列，存在长期协整的可能性。进一步进行协整分析，价差序列的平稳性如下：在1%的置信水平下，5分钟和1分钟数据的回归方程的残差为平稳，日数据、60分钟及30分钟数据的回归方程的残差则在5%的置信水平下

为平稳；15分钟数据的回归方程残差在10%的置信水平下为平稳的。可见，中国神华与中煤能源的价格在日数据和5个日内高频数据上均存在长期的协整关系，均具备统计套利的条件。对6个频率的价差Spread序列分别去均值进行去中心化处理，日数据、60分钟、30分钟、15分钟、5分钟及1分钟数据序列分别为：即 Spread-0.1057、Spread+0.0236、Spread+0.0108、Spread-0.0057、Spread+0.0002、Spread-0.0004分别得到Mspread序列。因此，采用单一协整模型运用日数据和5种日内高频数据对中国神华和中煤能源进行统计套利的交易信号具体发出规则如表2所示。

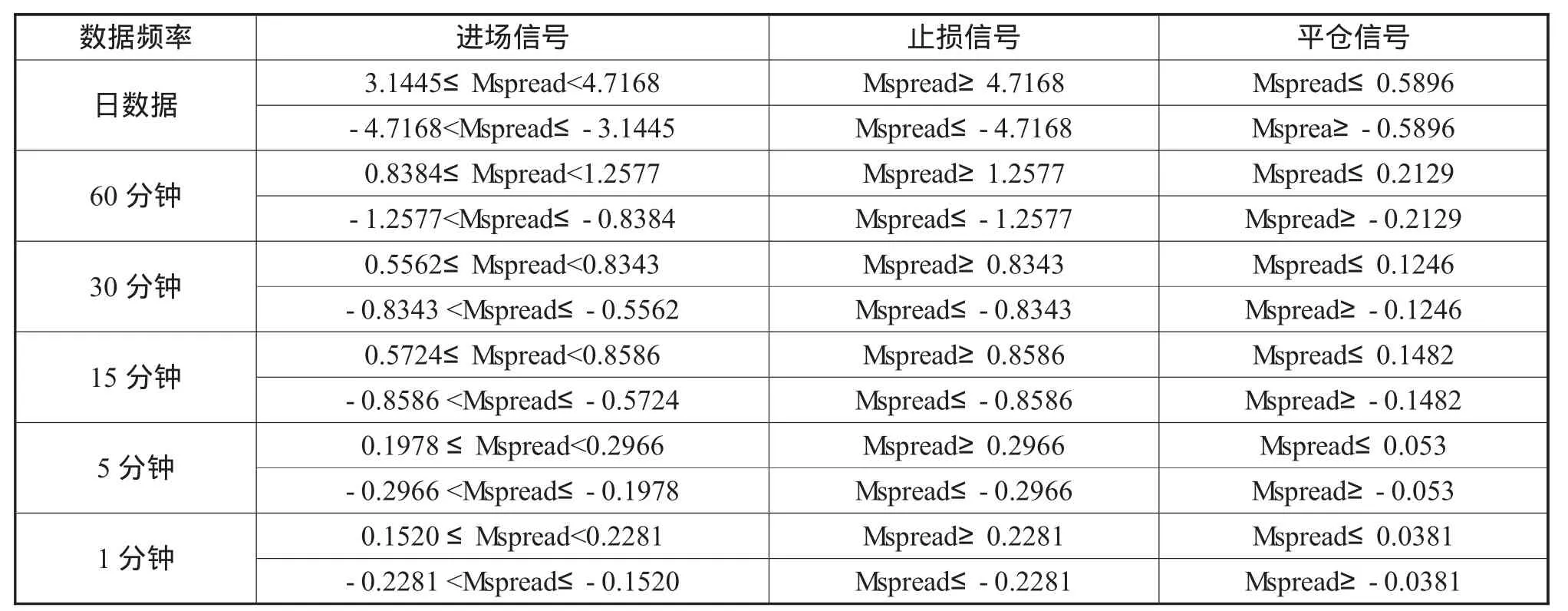
表2 基于协整模型的统计套利策略交易信号发出的具体规则

（2）基于卡尔曼滤波模型的统计套利策略交易信号发出的具体规则

通过协整分析发现，日数据、60、30分、15、5及1分钟数据的参数β依次为2.454235、2.479564、2.447274、2.430403、2.456503、2.448264，可见 β 参数确实存在时变性，因此将估计时变参数的理想模型——卡尔曼滤波模型引入到统计套利策略中，对β进行估计。卡尔曼滤波的分析结果表明：各个数据频率的量测方程的拟合程度都相当好，说明卡尔曼滤波分析是十分有效的。进一步计算价差序长期均值和标准差，并对其进行去中心化处理后，采用单一卡尔曼滤波模型运用日数据和5种日内高频数据对中国神华和中煤能源进行统计套利的交易信号的发出规则如表3所示。

表3 基于卡尔曼滤波模型的统计套利策略交易信号发出的具体规则

-0.2183 ＜Mspread≤-0.1455 Mspread≤-0.2183 Mspread≥-0.0364 5 分钟 0.1605≤Mspread＜0.2407 Mspread≥0.2407 Mspread≤0.0401-0.2407＜Mspread≤0.1605 Mspread≤-0.2407 Mspread≥-0.0401 1 分钟 0.1455≤Mspread＜0.2183 Mspread≥0.2183 Mspread≤0.0364

（四）组合策略的绩效评估

为了分析组合策略的有效性，将对单独采用协整模型或者单独采用卡尔曼模型的统计套利的绩效与采用组合策略的统计套利绩效进行比较分析。样本内外采用三种套利方案的绩效比较分别如表4、表5所示。

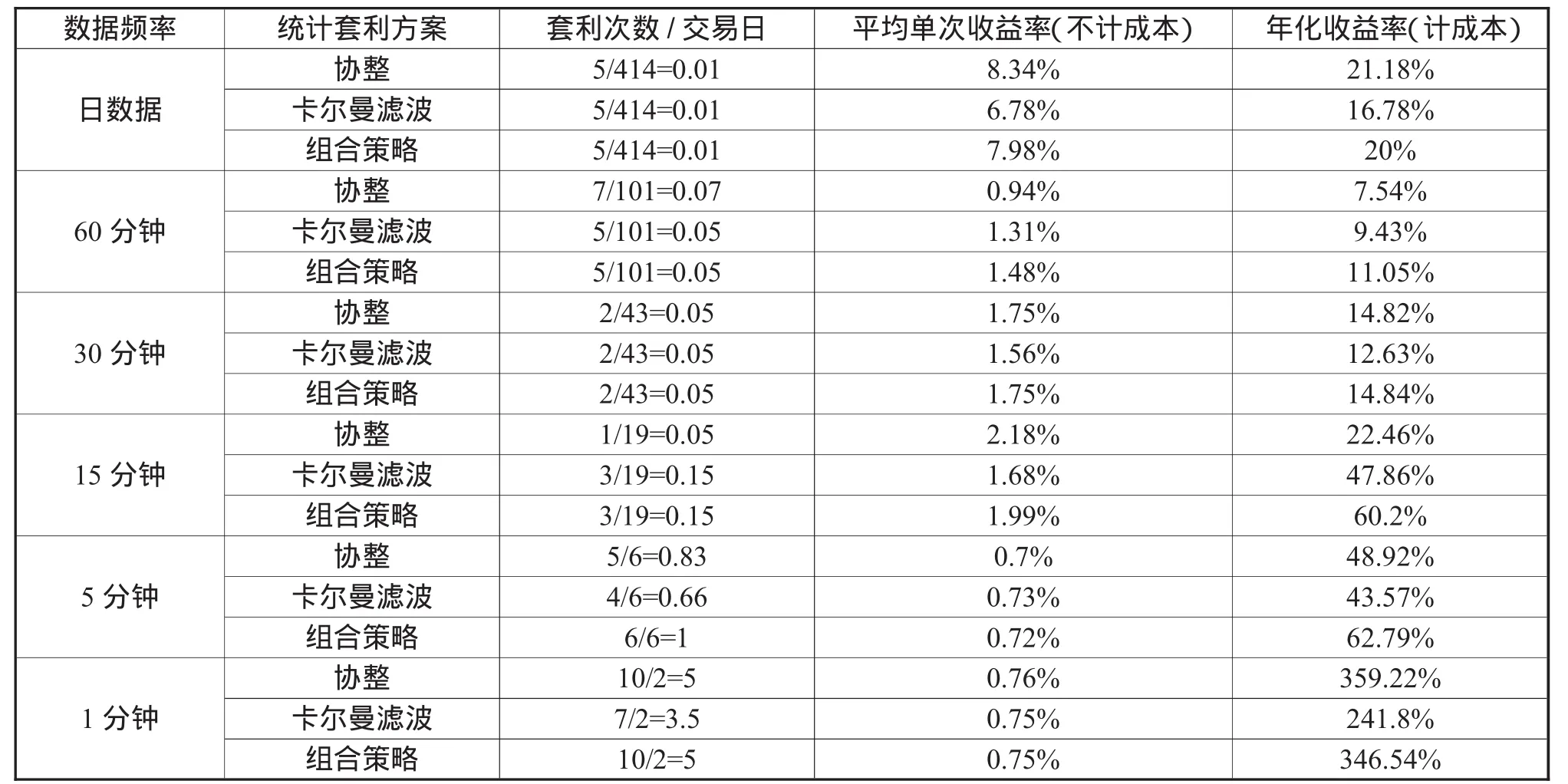
表4 样本内采用三种统计套利方案进行套利的绩效比较

表5 样本外采用三种统计套利方案进行套利的绩效比较

（1）组合策略的必要性分析

从表4可以看出，样本内，采用卡尔曼滤波模型与协整模型进行套利，各个频率数据套利的每交易日的交易次数、平均单次收益率均不存在一致变动现象；净年化收益率方面，采用卡尔曼滤波模型与协整模型运用各频率数据进行套利时，两模型效果存在轮流优劣现象。

从表5可知，样本外，采用协整模型与卡尔曼滤波模型用于统计套利，各频率数据进行套利时，发出交易信号的次数除了5分钟数据卡尔曼滤波模型显著高于协整模型外，其余各频率的交易信号次数均相同；并且两个模型在平均单次收益率方面也无明显优劣之分；在净年化收益率方面，运用日数据、30分钟、15分钟数据时，协整模型与卡尔曼滤波模型效果相同；运用60分钟及5分钟数据时，卡尔曼滤波模型优于协整模型；运用 1分钟数据时，协整模型优于卡尔曼滤波模型。

综合样本内外卡尔曼滤波模型与协整模型在统计套利策略中的绩效，引入的卡尔曼滤波模型应用于统计套利策略中是有效的，但其与协整模型相比，在各频率数据上均不存在明显的优劣之分，由于不同频率数据对应不同时间段，可见模型效果存在时变性。因此组合策略是必要的。

（2）组合策略的收益性分析

从表4可以看出，样本内，采用组合策略运用各频率数据进行统计套利时，在平均每交易日的套利次数方面，基本上大于（15、5分钟数据）或者接近（日数据、30、1分钟数据）采用单一模型进行套利时的发出进场信号较多的模型，仅运用60分钟数据时除外；在平均单次收益率方面，也基本上大于（60分钟）或者接近（日数据、30、15、5分钟数据）采用单一模型进行套利时的平均单次收益率较高的模型，仅运用1分钟数据时除外（由于采用1分钟进行套利，交易成本影响过大，因此不计）。可见组合策略达到了增加交易机会及扩大单次收益率的目的。在净年化收益率方面，采用组合策略运用各频率数据进行统计套利时，全部大于（60、30、15及5分钟数据）或者接近（日数据和1分钟数据）采取单一模型进行套利时年化收益率较高的模型，可见其达到了提高整体收益率的目的。因此，样本内，采用组合策略进行统计套利显著优于采取单一模型的策略。同时，我们仍要考虑组合策略在样本外的绩效，分析组合策略在样本外的有效性。

由表5可知，在样本外，采用组合策略，运用6个频率数据进行统计套利时，由于日数据和15分钟数据价差在均值附近波动，没有出现套利机会，采用60分钟、30分钟、5分钟及1分钟数据套利时可分别获得14.73%、39.92%、76.56%及-123.48%的净年化收益率。并且组合策略下交易信号的准确性得到了很好的体现，由于数据较少，样本外两模型的绩效仅在5分钟数据上有显著区别，此时卡尔曼滤波模型显著优于协整模型，而组合策略的绩效则接近较优的卡尔曼滤波模型绩效，可见组合策略能综合利用两模型的优势在5分钟数据上得到了很好的体现。

（3）组合策略的风险性

由于以上分析均是从收益率方面来考虑的，仍需综合考虑风险因素，采用最为广泛使用的夏普比率对该统计套利策略进行评价。夏普比率=（Rp-Rf）/σp其表示投资组合承担单位风险可获得的风险收益率与无风险收益率的差值。其值越大，说明收益率对承担风险的补偿程度越高，投资组合绩效越好，而其值为负时，则大小排序不具意义。Rp、Rf分别表示套利组合收益率和无风险收益率，其中无风险收益率本文采用一年期定期存款利率2.25%；σp表示套利组合收益率标准差。又因统计套利策略是一个市场中性策略，基于该策略产生的投资组合收益率对市场收益率的敏感程度也是衡量统计策略表现的指标。根据资本资产定价模型（CAPM模型），E（Rp）=Rf+β'[E（Rm-Rf）]，用β'（非前文协整分析中的β）系数表示。本文建立回归方程Rp=α+β'Rm+ε，运用最小二乘法来计算β'。

采用组合策略构建的套利组合及沪深300指数的夏普比率及β'如表9所示。其中套利组合的夏普比率均考虑了交易成本及费用，而沪深300指数则均未考虑交易成本及费用。

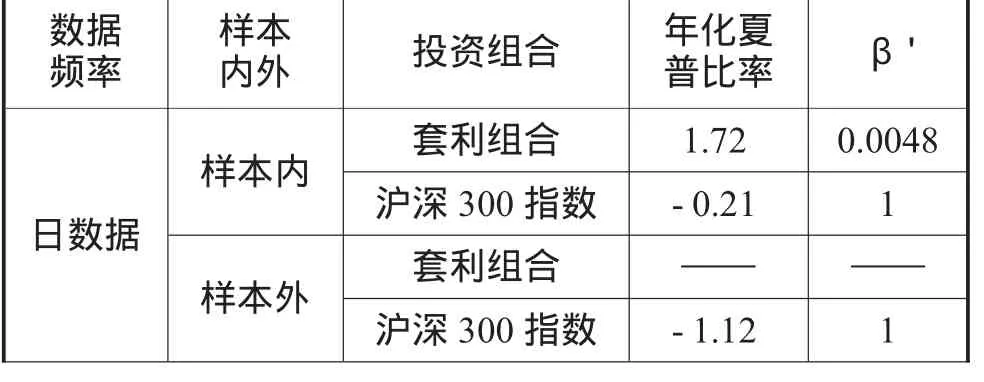
表6 基于组合策略的套利组合及沪深300指数的夏普比率与β'

沪深300指数样本外 套利组合60分钟样本内 套利组合沪深300指数沪深300指数30分钟样本内 套利组合沪深300指数样本外 套利组合样本外 套利组合-10.40 1.18 1.43-1.73-3.87 2.08-3.03 3.33-4.56-0.0082 1-0.0153 1 0.0183 1-0.0391-0.2382 1沪深300指数 -1.78 1样本内 套利组合 4.20 -0.0331 5分钟样本内 套利组合 5.05 0.0447沪深300指数 -2.16 1样本外 套利组合 4.88 0.0648沪深300指数 -2.94 1 1分钟样本内 套利组合 11.47 0.0633沪深300指数 0.64 1 15分钟 沪深300指数 -2.84 1样本外 套利组合 — —沪深300指数 -8.06 1

由表6可知，样本内，在计成本费用后，组合套利策略在各频率数据的夏普比率均大于1，说明均有投资价值，采用15、5及1分钟数据时的夏普比率分别高达4.20、5.05及11.47，可见风险收益率很好地补充了其所承担的风险，随着数据频率提高，年化夏普比率不断增大；而未计成本费用的沪深300指数在各频率数据（除1分钟数据外）的夏普比率均为负，而采用1分钟数据的夏普比率为0.64，小于1，说明沪深300指数在该研究期间不具投资价值，组合统计套利策略显著优于指数投资策略。并且套利组合在各频率数据上的 的绝对值均小于0.01，接近于0，可见组合统计套利策略是市场中性的，能很好地免疫市场风险。

样本外，计成本费用后，组合套利策略在各频率数据（除1分钟数据外）的夏普比率均大于1，说明均有投资价值，采用30分钟及5分钟数据时的夏普比率分别高达3.33及4.88，可见风险收益率很好地补充了其所承担的风险，并且在该策略下运用较高频率的数据大体上比较低频率的数据进行套利所获得的夏普比率较高，而且采用较高频率数据进行套利时，其套利期限较短，即使和较低频率获得的年化收益率相同，其也能分步实现收益率利于资金管理运用，因此较优；而不考虑交易成本及费用时，沪深300指数在各频率数据的夏普比率均为负，说明沪深300指数在该期间不具投资价值，组合统计套利策略仍然明显优于指数投资策略。并且套利组合在各频率数据上（除1分钟数据外）的 的绝对值均小于0.01，接近于0，可见组合统计套利策略是市场中性的，而采用1分钟数据的 为-0.24，远小于1，对市场风险的敏感性很低。

四、结论及展望

本文将组合预测思想引入到统计套利策略中，并利用日数据和五种日内高频数据进行了实证研究。结果表明：（1）考虑到金融时间序列模型参数的时变性而引入的卡尔曼滤波模型应用于统计套利策略是有效的，但其与传统协整模型并不存在明显优劣之分，因此组合策略是必要的。（2）组合策略达到了增加交易机会及扩大单次收益率从而提高整体收益率的目的。样本内，采用组合策略进行统计套利显著优于采取单一模型的策略。在样本外，组合策略交易信号的准确性及综合利用各模型的优势也得到了很好的体现，考虑交易成本及费用后，可获得可观收益率。（3）综合考虑风险因素，采用夏普比率及敏感系数对该组合策略进行评价得出，样本内外，在考虑了交易成本及费用的情况下，组合套利策略在各频率数据的夏普比率均大于1，说明均有投资价值；且采用高频数据的夏普比率更高，收益率更稳定。（4）各频率数据（除样本外1分钟数据）的绝对值均小于0.01，近似于0，接近市场中性的，而样本外采用1分钟数据的 为-0.24，远小于1，对市场风险的敏感性很低，可见组合统计套利策略独立于市场行情，能很好地免疫市场风险。

［1］Bolgun，Evren，Kurun，Engin and Guven，Serhat.Dynamic Pairs Trading Strategy For The Companies Listed In The Istanbul Stock Exchange [J].Working papers，2009

［2］ J Low.Equity Market Neutral：Diversifier Across Market Cycles[J].CREDIT SUISSE ASSET MANAGEMENT，2009

［3］WK Bertram.Optimal trading strategies for It?diffusion processes[J].Physica A，2009（388）：2865～2873

［4］方昊，统计套利的理论模式及应用分析——基于中国封闭式基金市场的检验[J].统计与决策，2005：14～16

［5］韩广哲，陈守东.统计套利模型研究——基于上证50指

［6］常宗琪.白糖统计套利理论模式研究及实例分析[J].经济师，2008（11）：30～31

［7］仇中群，程希骏.基于协整的股指期货跨期套利策略模型[J].系统工程，2008，26（12）：26～29

［8］徐光梅.从成对交易到动量检验——统计套利的学习与应用：[硕士学位论文].浙江：浙江大学，2008

［9］刘华.基于统计套利ETF期现套利方法应用研究：[硕士学位论文].大连：大连理工大学，2008

［10］张波.不完全信息下基于卡尔曼滤波的投资决策：[硕士学位论文].哈尔滨：哈尔滨工业大学，2008

［11］王苏生，王丽，陈搏，刘艳.基于卡尔曼滤波的期货价格期限结构模型[J].运筹与管理，2010，19（1）：113～118

［12］吴虹，尹华.ARIMA与SVM组合模型的石油价格预测[J].计算机仿真，2010，27（5）：264～266

［13］腾格尔，何跃.基于GMDH组合的中国GDP预测模型研究[J].统计与决策，2010（7）：17～19

［14］张伟，廖益琴.基于变权重组合模型的中国股市波动率预测经济[J].研究导刊，2010（4）：27～28

［15］杨怀东，伍娟.基于高频数据的成对交易统计套利策略实证研究.第五届中国管理学年会，2010.11