梯形嵌套加密截断有限元方法及收敛性分析
王雪玲,王奇生
王雪玲,王奇生
(五邑大学 数学与计算科学学院,广东 江门 529020)



考虑二维Poisson方程齐次边界条件的第一边值问题[4]




1 梯形嵌套加密方法简介

图1 标准单元
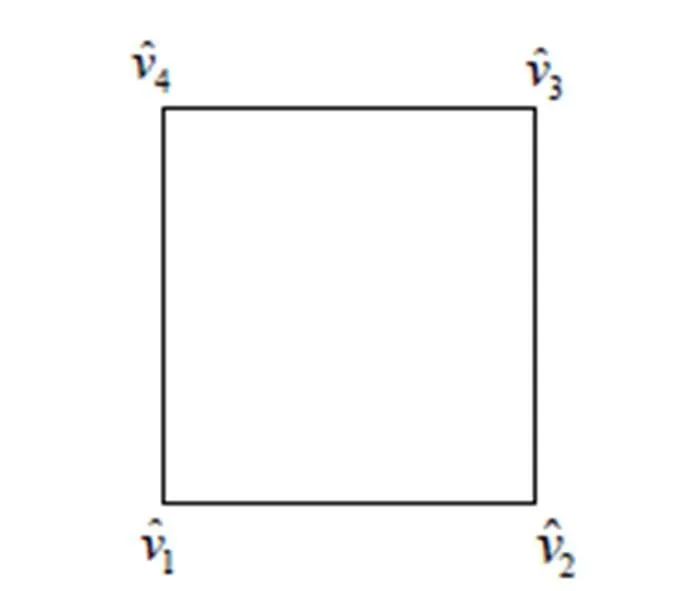
图2 参考单元
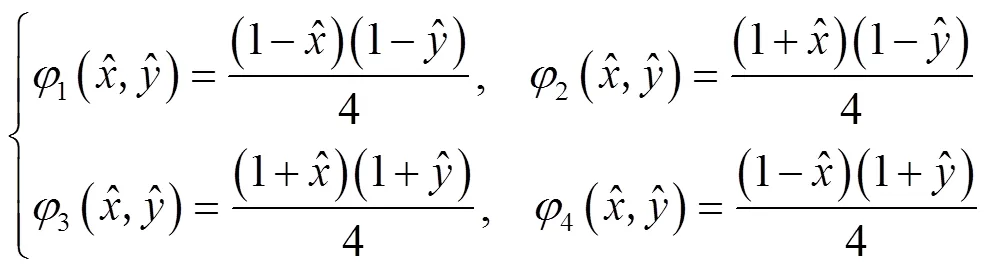
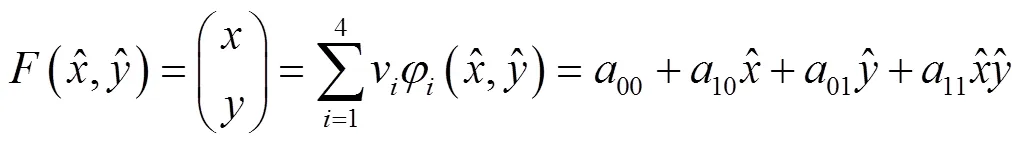
其中




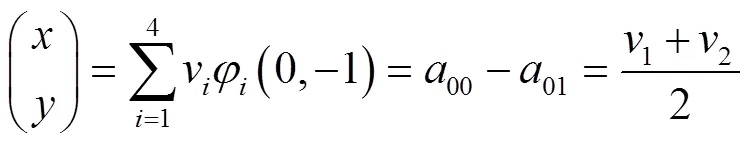


图3 梯形嵌套加密


一般地,有








和
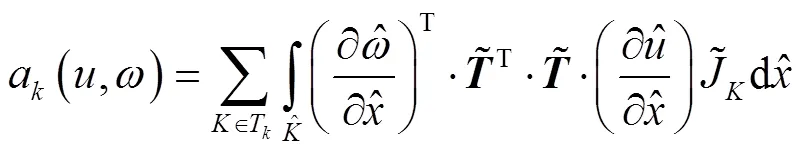
于是有
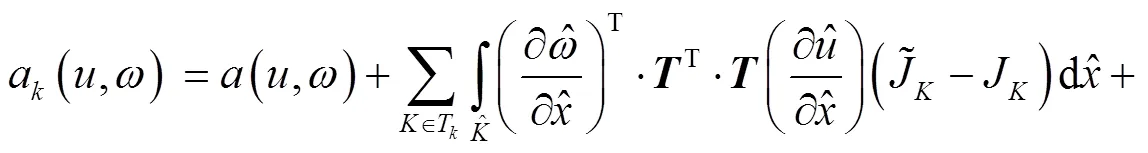






又由式(13)和式(15)可得,

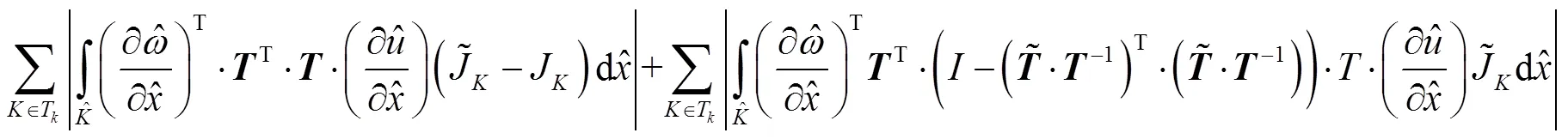

即


所以得估计式



故


从而


即有

所以得估计式

定理1证明完毕.

证明 由定理1的证明过程,很容易得到




证明 由Strang第一引理(参见文献[7]中定理4.1.1)
.
再由定理1和定理2,定理3得证.
[1] ZHANG Shangyou. On the nested refinement of quadrilateral and hexahedral finite elements and affine1 approximation [J]. Numer Math, 2004, 98: 559-579.
[2] ZHANG Shangyou. Numerical integration with Taylor truncations for the quadrilateral and hexahedral finite elements[J]. Journal of Computational and applied Mathematics, 2007, 205: 325-342.
[3]WANG Qisheng, WANG Xueling. Convergence analysis and the nested refinement for the trapezoid finite element[J]. Advanced Materials Research, 2011, 317-319: 1921-1925.
[4] 林群,严宁宁. 高效有限元构造与分析[M]. 保定:河北大学出版社,1996.
[5] 李荣华. 偏微分方程数值解法[M]. 北京:高等教育出版社,2005.
[6] 陈传淼,黄云清. 有限元高精度理论[M]. 长沙:湖南科学出版社,1995.
[7]CIARLET P G. The finite element method for elliptic problems[M]. Amsterdam North-Holland: 1978.

WANG Xue-ling, WANGQi-sheng
(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)


1006-7302(2012)02-0008-07
O241.82
A
2011-11-28
广东省自然科学基金资助项目(104529001005845)
王雪玲(1986—),女,河南商城人,在读硕士生,研究方向为微分方程数值解法;王奇生,教授,博士,硕士生导师,通信作者,研究方向为微分方程数值解法.

