图的色数与着色数的上界
史小艺,张宁,薛婷婷
图的色数与着色数的上界
史小艺,张宁,薛婷婷
(中国矿业大学 理学院,江苏 徐州 221116)

无向图;色数;着色数;围长

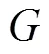

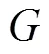

1 主要引理



2 主要结果
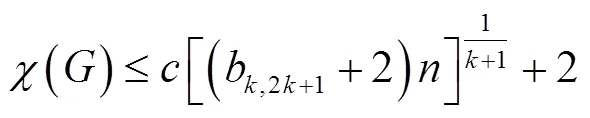

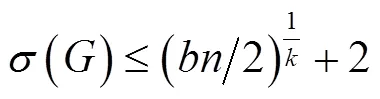
[1] JENSEN T R, TOFE B. Graph coloring problems[M]. New York: John Wiley &Sons, 1995.
[2] CHUNG F. Open problems of Paul Erdos in graph theory[J]. J Graph Theory, 1997, 25: 3-36.
[3] SPENCER J. Asymptotic lower bounds for Ramsey functions[J]. Discrete Math, 1997, 20: 69-76.
[4] ZAKER M. New bounds for the chromatic number of graphs[J]. J Graph Theory, 2008, 58: 110-122.
[5] EROS P, HAJNAL A. Chromatic number of finite and infinite graphs[J]. Discrete Math, 1985, 53: 281-285.
[6] ZAKER M. Bounds for chromatic number in terms of even-girth and booksize[J]. Discrete mathematics, 2011, 311: 259-270.
Bounds for Chromatic and Coloring Number of Graphs
SHIXiao-yi, ZHANGNing, XUETing-ting
(College of Sciences, China University of Mining and Technology, Xuzhou 221008, China)
undirected graph; chromatic number; coloring number; girth
1006-7302(2012)02-0015-03
O157.5
A
2011-10-21
中央高校基本科研业务费专项基金资助(2010LKSX06)
史小艺(1986—),女,江苏沛县人,在读硕士生,研究方向为图论及其应用.

