常型Sturm-Liouville算子特征值的渐近式和迹公式

陈莉敏



常型Sturm-Liouville算子特征值的渐近式和迹公式

陈莉敏

（常州工程职业技术学院 基础部，江苏 常州 213164）

应用迭代法计算了自伴型Sturm-Liouville微分算子特征值的渐近式，据此给出了算子的一类迹公式，并计算出其正则项和迹量.

Sturm-Liouville算子；特征值；迹公式

1 引言及预备知识

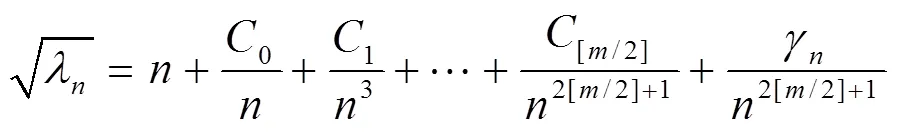
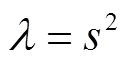
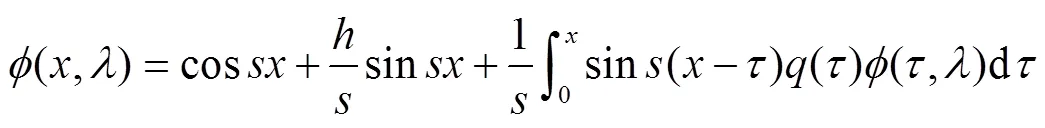
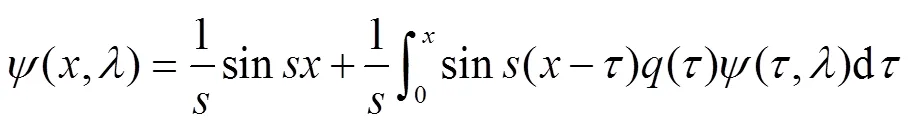
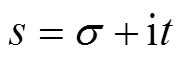
定理1[3]55自伴边条件下的特征值都是实的.

2 主要结果及其证明

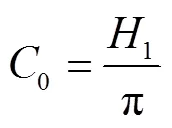
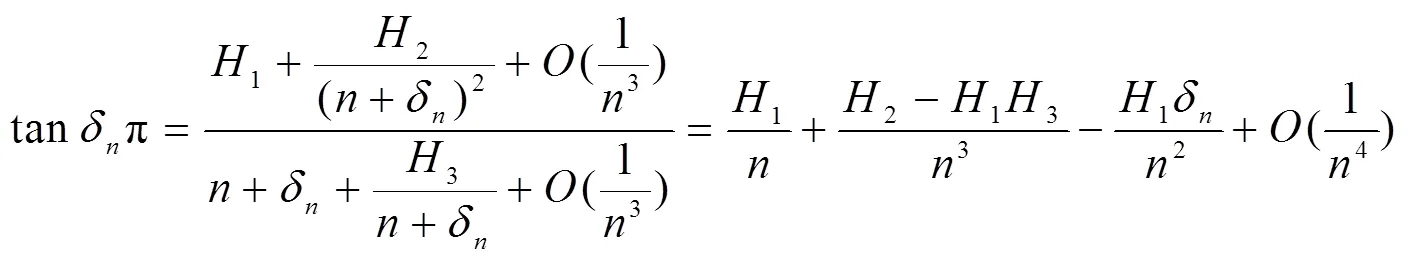
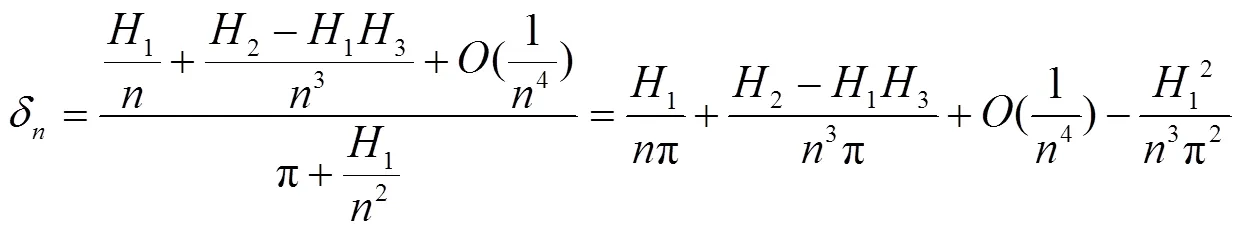
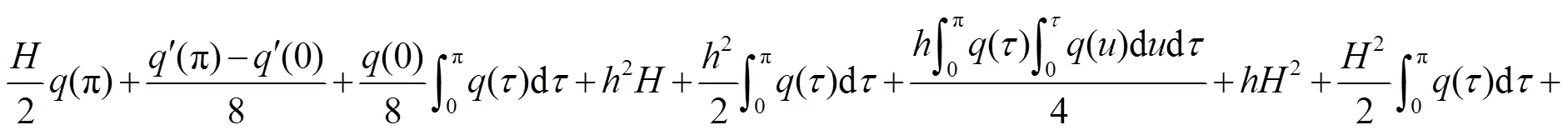
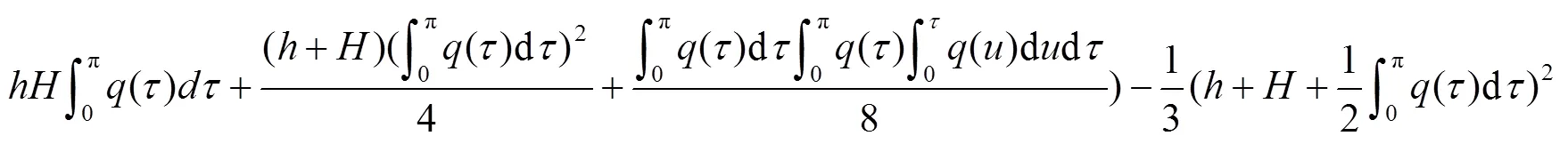
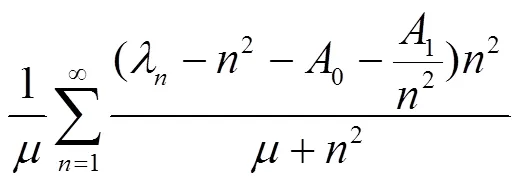
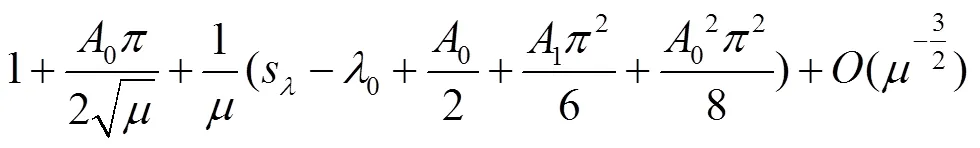
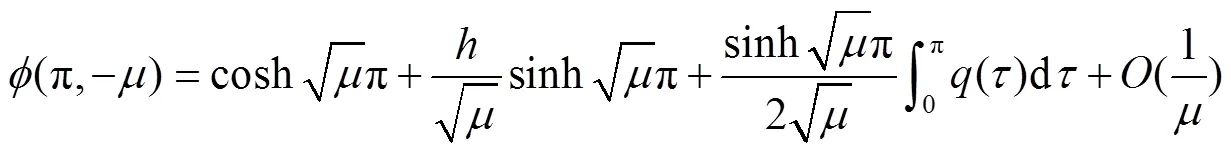
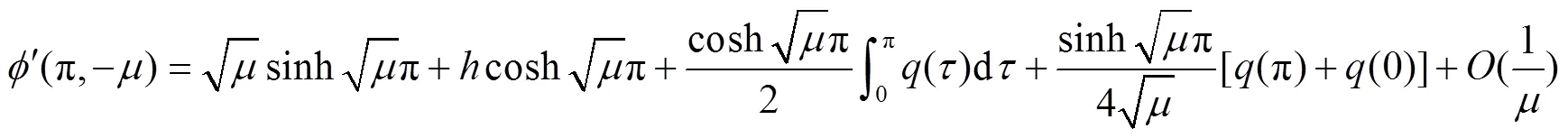
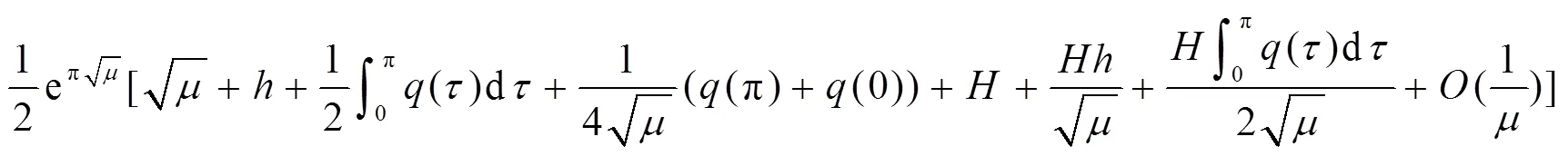
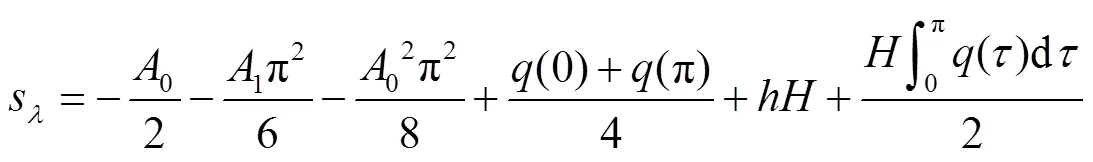
[1] ATKNSON F V. Discrete and continuous boundary problems[M]. New York: Academic Press, 1964.

[2]EATHEMATICA S P. On the location of spectral concentration for Sturm-Liouville problems with rapidly decaying potential[J]. Mathematica, 1998, 45: 23-36.

[3]刘景麟. 常微分算子谱论[M]. 北京：科学出版社，2009.

[4]LEVITAN B M, SARGSJAN I S. Sturm-Liouville and Dirac operators[M]. Dordrecht: Kluwer Academic Publishers, 1991.

An Asymptotic Expression and Trace Formula of Eigenvalues for Sturm-Liouville Operators

CHENLi-min

(Department of Basic Courses, Changzhou Institute of Engineering Technology, Changzhou 213164, China)

The coefficients in asymptotic formulae of eigenvalue for Sturm-Liouville operators with self-adjoined boundary condition are calculated, and on the basis of this, a new trace concept and its expressions are introduced.

Sturm-Liouville operators; eigenvalues; trace formulae

1006-7302（2012）02-0025-04

O175

A

2011-11-08

陈莉敏（1977—），女，江苏扬州人，讲师，硕士，研究方向为微分方程.