宇宙空间的变模分析
冯彪
宇宙空间的变模分析
冯彪
(湛江技师学院 职业教育研究所,广东 湛江 524037)
通过分析宇宙空间的测模变化和变模效应,论述了宇宙质量、能量的可测性起源,指出各种物质形态和能量变化均是时空流形不同结构的具体表现形式,只有研究清楚时空流形的拓扑结构和可拓变换才能掌握宇宙万物的变化发展规律.
宇宙空间;球面空间;时空流形;变模分析
1 欧几里得空间与球面空间
欧几里得空间简称欧氏空间,笛卡儿坐标系、极坐标系、球坐标系都可描述一个欧氏空间,同一个欧氏空间中的坐标系可进行坐标变换. 在欧氏空间的基础上,牛顿将绝对时空观发展成为物理学的经典时空观,并以之作为人类认识世界基本形式和理解科学理论的思维基础. 欧氏几何学反映的经典时空结构是均匀的、平直的,绝对时空观认为空间、时间脱离物质及其运动而客观存在.
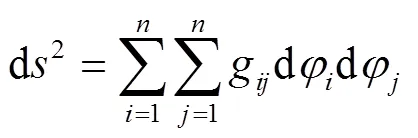
二维欧氏空间的平面不能包容二维球面:同理,三维欧氏空间不能包容三维球面空间,其需用四维欧氏空间包容. 事实上,人类不能直观感觉三维球面被四维欧氏空间包容的关系,因此,人类也不能直接观测自身所处的时间四维球面空间被五维欧氏空间所包容的等价关系,这需要通过测量物质的质量、能量等运动效应来间接认识宇宙球面空间的时空结构.
2 宇宙空间是时空四维球面空间

测量是一种比较(对比),人类认识的实践性体现在对客观对象的可测性(可操作性)上. 时间和空间作为物理学的基本量,其可测的前提是具有时空效应的差异性. 人类能直观感知的空间维度是欧氏时空四维,人类可测的宇宙空间是不超过五维的欧氏时空. 根据球面空间与欧氏空间的坐标变换关系,(弯曲的)四维球面空间等价于(平直的)欧氏五维空间,由此可知,人类所处的宇宙空间是时空四维球面空间.
按球面空间的定义,式(1)确定的空间是四维球面空间,
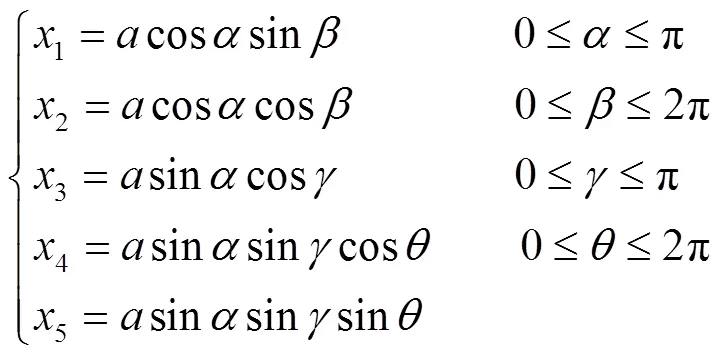
其相应的时空四维宇宙球面空间可用式(2)表示.
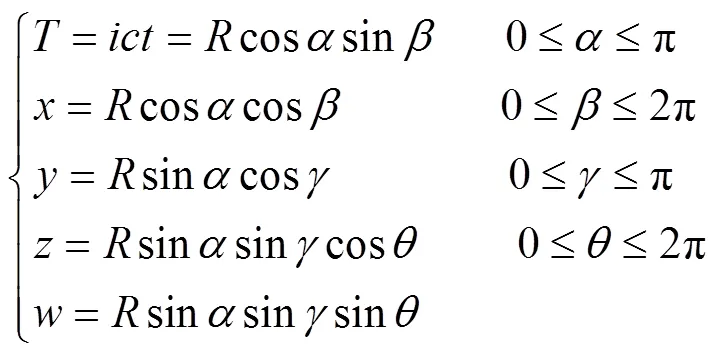
由(2)式得雅可比行列式:

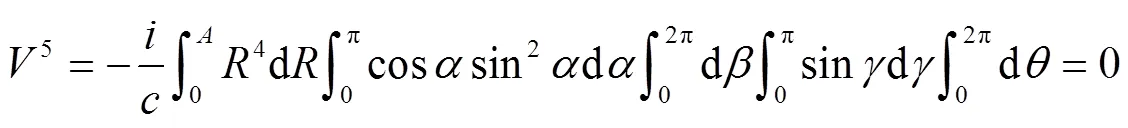
时空四维球面空间的面积(体积)
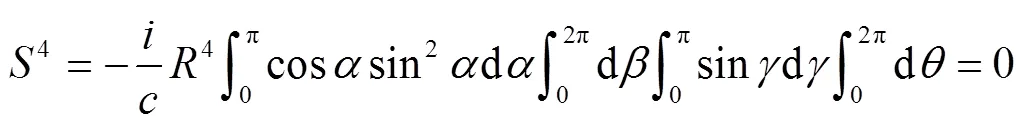
由式(4)、式(5)知,宇宙中任何一个观测者对时空四维宇宙球面空间的测度是互相抵消的,在总体上等于零(或说是虚无),即宇宙集为零测集.
3 可测性与测模
测量是对客观对象进行可操作性的比较(对比),可测性的精度显示差异化的表现程度. 事物的质由量构成并用量描述,量是可测的,可测性的量度由测模决定. 根据测模的定义,由式(2)所确定的时空四维宇宙球面空间测模的微分形式是:

时间和空间的“定性定义”和“定量定义”与测模紧密相连,运动(速度)是空间维度相对于时间维度的变化率,质量和能量等可通过运动效应来表现. 可测是一种客体到主体的映射,事物的实在性等价于可测性,只有可观测的量才是存在的;量纲是测量参数的转换,量子则是测量的基元(实在). 物理学的研究表明,客观对象(如原子)往往不是人的感官所能直接观测和认识的,而是需要借助复杂的科学仪器间接观测的,但在这一过程中势必引入导致客体本身发生变化的干扰或影响,从而产生观测误差,导致“波粒二象性”问题.
人类能直观感觉生活在三维空间和一维时间中,由于四维时空不能包容五维欧氏时空,故难以直观感觉空间的弯曲而只能通过变模效应来测度. 变模效应的表现形式之一是质量、能量对时空流形的改变. 由于宇宙集为零测集,故时空四维宇宙球面空间为局部可测空间,也存在不可测的部分;任一观测者对负空间的不可测性是宇宙对称性产生破缺(宇称不守恒)的根本原因.
3.1 光速不变与观测极限
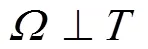
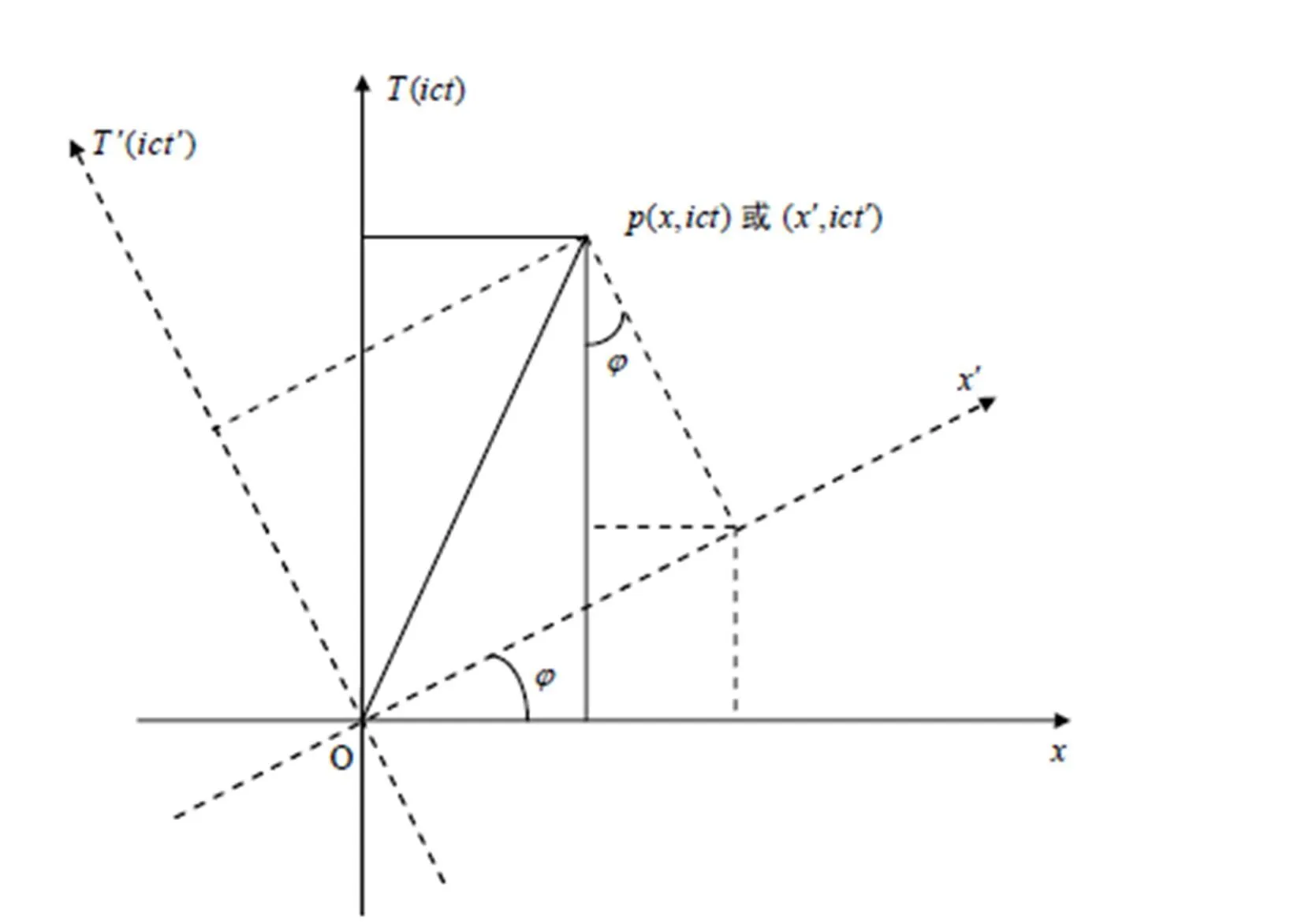
图1 观测系的旋转变换关系


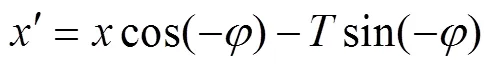


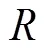
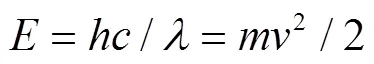
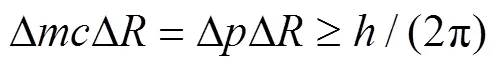
这就是海森堡测不准原理(不确定性原理)的表达式(实践中,式中的等号“=”视可测性精度取约等号“≈”).
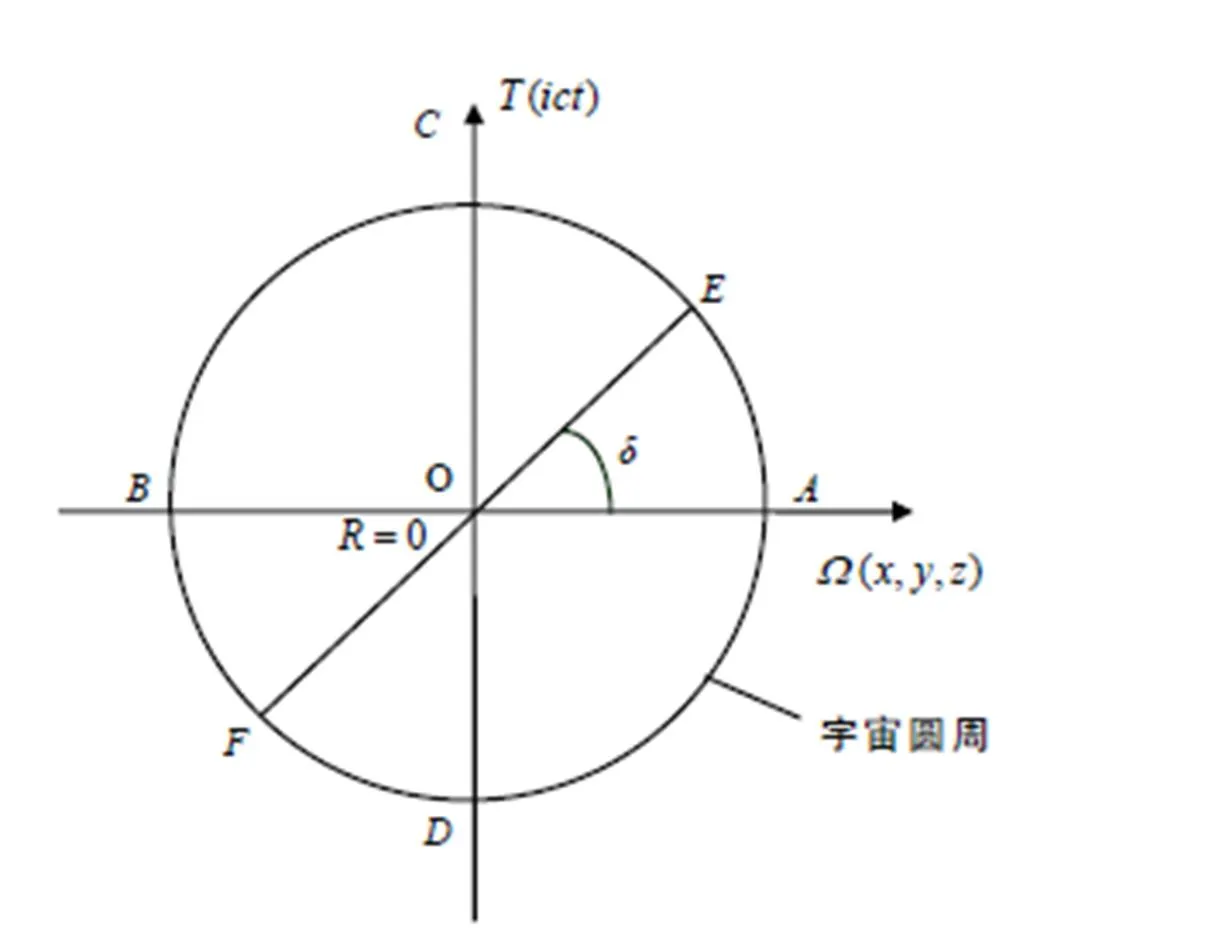
图2 宇宙圆周示意图
3.2 测模与红移现象
对于大于三维的高维空间,可借助“投影法”来解析. 即将时空四维宇宙球面空间(等价于五维欧氏时空)理解为光子(光波)作宇宙圆周运动,其在直径上的投影(简谐振动)使弯曲的球面空间化为平直的欧氏空间,以达到降维的目的. “化曲为直”(五维降为四维)的简谐振动属于周期性运动,光子的运动以质量、能量等形式产生变模效应,由此可以通过变模效应分析宇宙万物的时空结构.


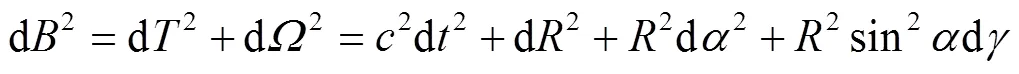

将式(11)和式(15)代入式(17),得:

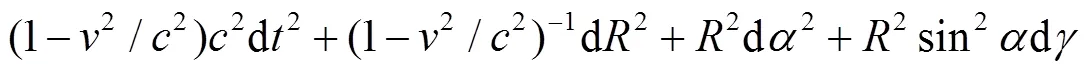
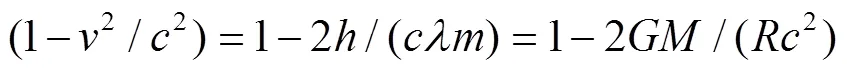
实验已证实,引力场使光源红移. 比如,太阳表面比地球表面的引力场强大,与氢在地球表面产生的光谱相比,它在太阳表面产生的光谱发生了红移. 由于光源红移,使观察者觉得光源物质的物理结构和性质也随之发生了变化,即观测值是观测者所处状态的函数. 观测者觉得自己处于正物质世界的引力中心,离引力中心越远的宇域内包括的正物质越多则宇域边上的引力场越强,红移量越大,这是宇宙远处离观测者越远红移量越大的原因. 如果已知显示红移处与观测者的距离和红移量,就可计算得出这个宇域内的物质质量,也可根据物质的质量和红移量计算出观测者处与显示红移处的距离.
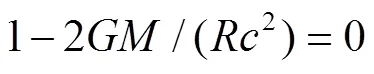

万有引力场效应导致了红移,观测者觉得自己所处的位置是万有引力中心,离中心越远其引力势越大、红移效应越大. 由于越远处红移越大,因此越远处的星系越难观测,任何观测者所观测到的宇宙星系不可能超过整个宇宙星系的一半.
3.3 测模与质量(惯性)
人类对客观世界的认知来源于客体的可测性. 由物理实验的观测可知,对时空四维球面空间,人们是在欧氏空间(平直空间)的基础上加上质量或能量的运动(变模)效应来认识的. 时空四维宇宙球面空间本身不存在中心点,观测者以其所处位置作纯几何中心点(不动点)从而使时空四维宇宙球面空间的各点具有了差异性.
一切物质形态均是时空流形的表现形式,均是时空的函数. 换言之,物质就是时空,物质的运动是时空流形在时间维度上的差异,这种差异具有可测性(测模),而质量和能量就来源于弯曲时空中测模的可测性. 物理量是量度物质的属性和描述其运动状态时所用的各种量值,例如,质量是量度物质惯性的物理量,质量等价于惯性,爱因斯坦把引力质量等于惯性质量称为等效原理. 根据式(20)有:
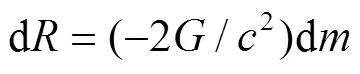
可见,质量是时空曲率半径(流形惯性)的量度.
由实验知,一对正、反物质的电子可同时由一对光子相会合而产生,p介子可变为电子和光子等粒子,电子在构成p介子的结构中做接近于光速的运动以形成比电子质量重得多的p介子静质量. 其他重粒子的静质量可类似产生,质子、中子等可变为p介子和电子等粒子. 由于光源的发光频率取决于光源物质本身,因此,人们在感觉光源红移的同时觉得物质结构也发生了变化,在宇宙红移条件下正物质世界的人只能看见正物质世界的部分宇宙.
4 变模角与变模方式
根据测模值和变模角是否变化可将空间分为变模空间和常模空间. 常模空间的测模为定值,变模空间的测模为变量. 一个空间是否可作为常模空间,不以尺度大小为标准,而是要看其在某一范围内是否有统一的测模(不随观测者的改变而改变). 若有统一的测模,不论空间尺度有多大,都可作为一个常模空间;在时空测模不能统一的情况下,如果不能在实际中把变模角产生的变模效应忽略,则经典牛顿力学就不适用了,且不管其空间尺度多小都不能视为常模空间.
因变模角不同而在时空各维度产生的变模效应差异会引起不同的变模路径和方式,由此导致空间拓扑的分维和分形,这是宇宙万物变化发展具有无限可拓性的根本原因.
4.1 变模与量变和质变
事物的质由量刻画,而量由测模确定,测模的变化反映时空流形的弯曲特性. 物质的性质就是时空拓扑结构的性质,物质表现时空的弯曲,时空反映物质如何运动. 任一事物,其质有规定性而无确定性. 质性(质的规定)和量性(量的规定)是相对的,事物运动过程中的变量可分为质性变量和量性变量,可表示如下:
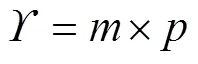
人类认识世界的逻辑顺序是先比较后归纳,反映在主观上,质是事物籍以比较的依据,如果没有质的存在,那么事物之间也就无法进行比较. 量也同质一样,是事物之间可以互相比较的依据;因此,质变与量变均可表示为运动的特性. 质变量变规律是变量的变化规律,事物是有限可分的而不是无限可分的,但在一定的边界极限时会产生模糊性,如物质由粒子性变成波动性,其确定性是无法“操作的”. 再如,在人类的实用领域里,常将极限当有限(不确定性看成确定性),牛顿、莱布尼兹等人创立的微积分正是将无穷小(并不等于0)当作零来处理,从而在工程上取得了巨大的成功[2].
另一方面,由于时间的有序性和空间的结构性引起事物的时空不相容性,使事物的“质的规定性”具有了层次. 事物的存在就是事物各个层次属性的综合,不同层次的规定就有不同层次的质,质的规定性也就是事物之间可区别的确定性. 质的规定性是由量的规定性来定义的,任何质的规定性都是由若干个“量”来表达,而任何“量”又都是由质来表述(定性)的. 质与量是相对而言的,低层次的质可用来定义高层次质的量. 事物运动变化的根本原因是测模的改变,由于测模具有可测性极限,因而万物新陈代谢也具有极限. 质变是事物某个层次质的变化,“度”是保持事物在某一层次上质的数量界限,物质在某层次上量的变化,如未到极限则不引起该层次质的变化.
4.2 变模拓扑与时空流形
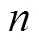
力是时空流形保持拓扑联系的表现形式,力的作用速度极限就是光速,不存在力的超距作用,作用量是一种量度,是时空流形固有的一种属性. 物质的各种表现形态是时空流形的不同弯曲形式,每一种形态就是一种拓扑结构,可以通过研究时空的拓扑结构来分析物质的结构和性质. 变模会导致变维,变模拓扑使时空维度的分维具有无限可能性(表现为分形结构的复杂性),故物质结构的变化具有无限可能性,这就是事物变化发展的动力.
5 结语
人类所处的宇宙空间是时空四维球面空间,光速极限和红移现象,将宇宙空间分为可测部分和不可测部分,可测部分的测模为正值称为正空间,人类生活于正空间,有正质量、正能量,不可测部分为负空间,有负质量、负能量,正负空间在总体上互相抵消,故宇宙集为零测集. 时空四维宇宙球面空间是变模空间,由于时空的运动效应(变模效应)将时空流形的惯性转化为质量、能量进而演变为各种形式的宇宙万物,物质的各种形态是时空结构的不同表现形式,事物量变质变的不同过程取决于时空结构的变模方式. 物质结构是时空流形的拓扑结构,事物变化发展具有无限性是因为时空拓扑结构具有无限可拓性. 因此,研究清楚时空流形的拓扑性质也就认识了宇宙万物的性质,通过分析时空结构的拓扑性质和变模效应就能掌握宇宙万物的变化发展规律.
[1] 冯彪. 物理空间的测度分析[J]. 五邑大学学报:自然科学版,2010, 24(1): 33-38.
[2] 冯彪. 数学中的极限与连续问题及其哲学涵义[J]. 保山师专学报,2009, 28(2): 20-22.
[3] 尤承业. 基础拓扑学讲义[M]. 北京:北京大学出版社,1997.
An Analysis of Modal Changes in Cosmic Space
FENGBiao
(Vocational Education Research Institute, Zhanjiang Technicians College, Zhanjiang 524037, China)
Through an analysis of changes in measurement modes and modal change effect, this paper discusses the measurable origin of cosmic mass and energy and points out that various matter forms and energy changes are concrete manifestation forms of different structures of the space-time manifold. Only when the topological structure of the space-time manifold and the extension transformation are made clear can the change and development law of the universe be mastered.
cosmic space; spherical space; space-time manifold; modal change analysis
1006-7302(2012)02-0029-08
O411.1
A
2011-09-30
冯彪(1967—),男,广东湛江人,高级讲师,硕士,研究方向为数学物理.

