一类分数阶微分方程多点边值问题解的存在唯一性

吴婷，顾长超



一类分数阶微分方程多点边值问题解的存在唯一性

吴婷，顾长超

（安徽大学 数学科学学院，安徽 合肥 230039）

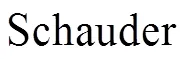
Caputo导数；边值问题；Green函数；不动点定理；存在性；唯一性

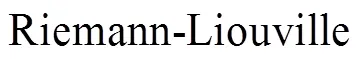
1 预备知识

利用不动点定理研究非线性分数阶微分方程多点边值问题

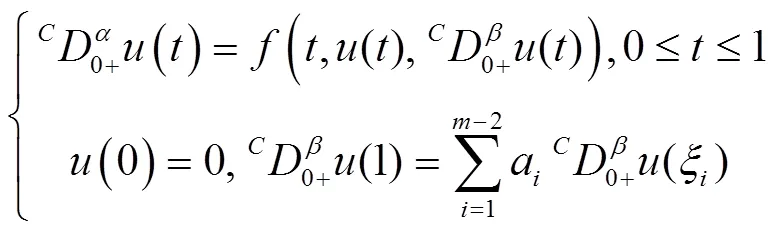
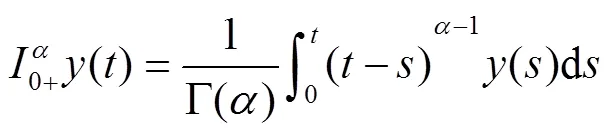
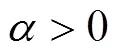
下面给出分数阶微分方程的Green函数.

有唯一解：

其中

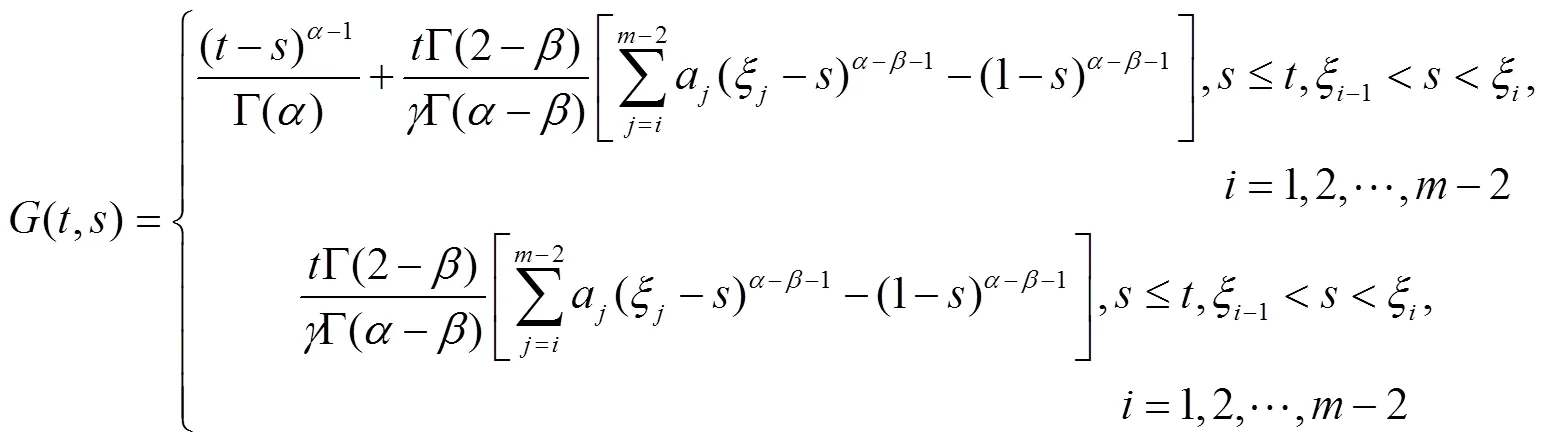
式（3）称作边值问题（2）的Green函数.

证明 由引理1和引理2，先将式（2）转化成等价的积分方程

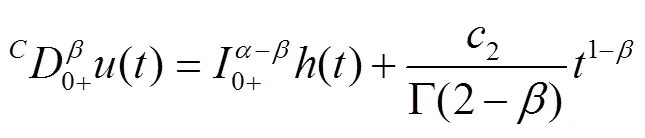
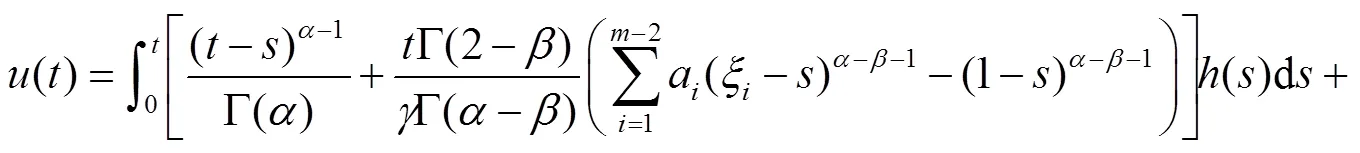
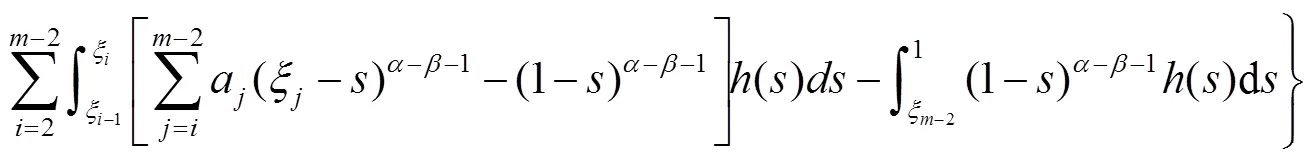
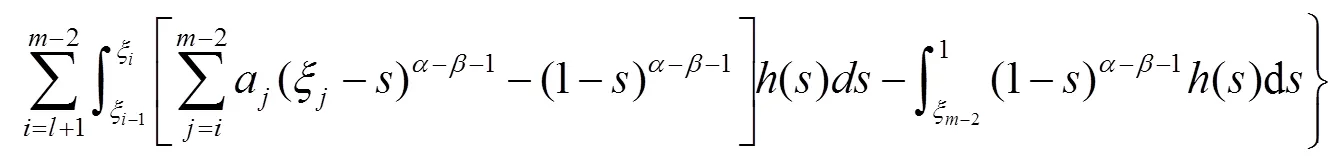
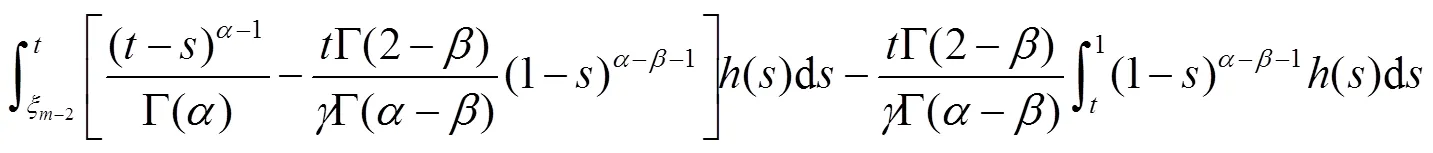
因此，式（2）的唯一解是

引理4 式（3）给出的Green函数满足下列性质：

2 主要结果

首先，给出以下条件：

为方便引入下面的记号

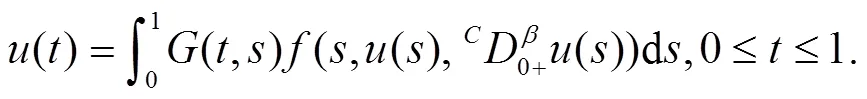
则有下面的结论：

从而得到

同时有

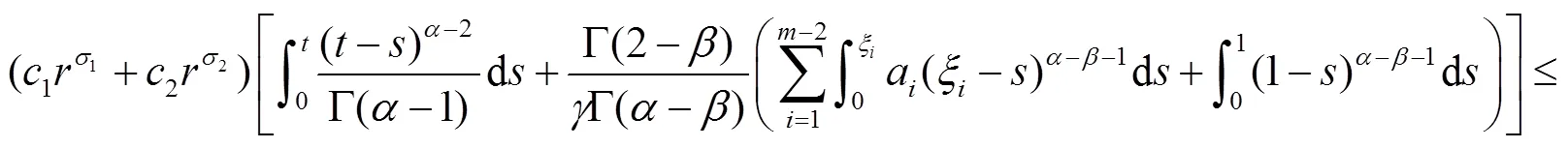
因此

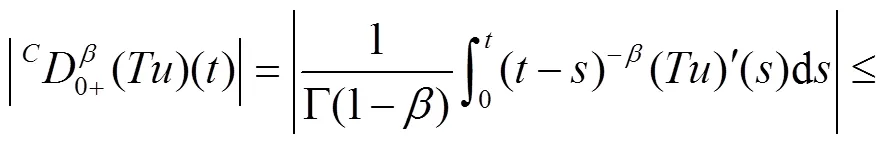
由范数的定义得

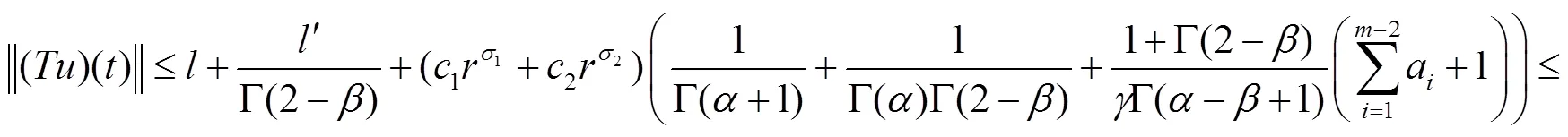
从而有

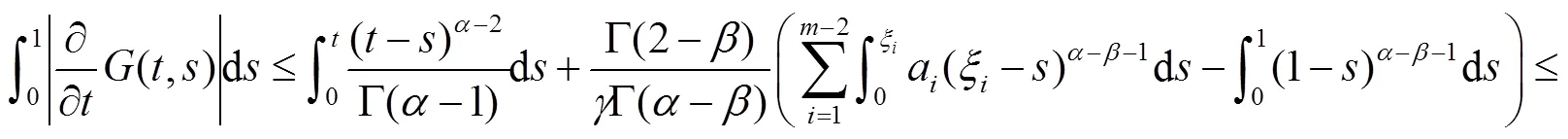
从而有

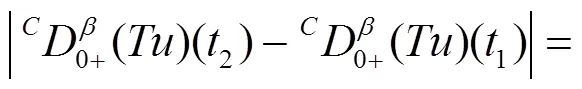
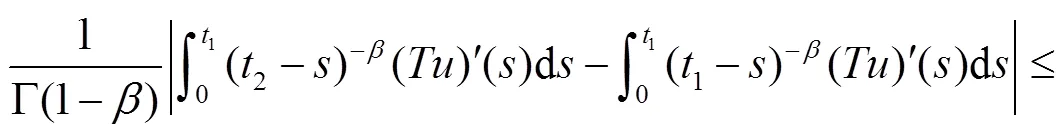
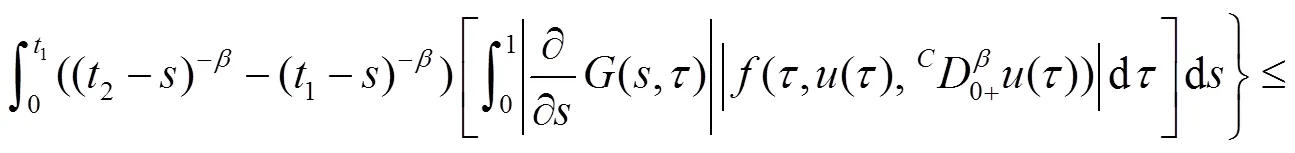
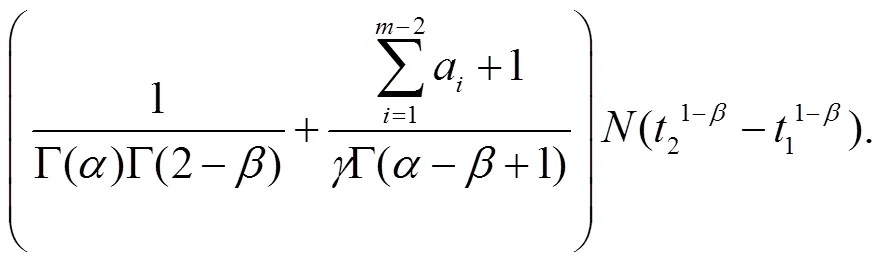
因此

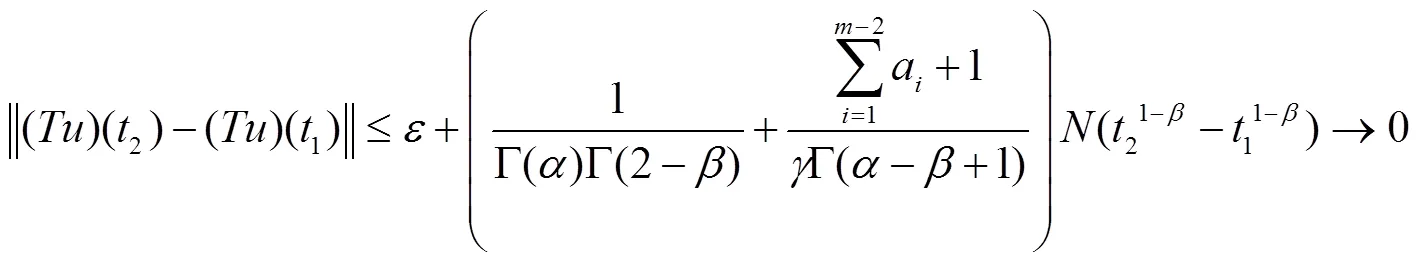
第二个结果是利用压缩映像原理得到边值问题（1）解的唯一性的一个充分条件：

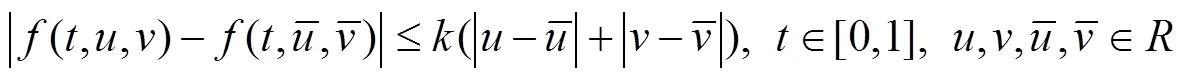
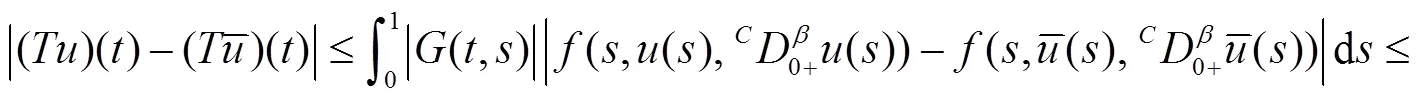
同时有

由压缩映像原理可知，边值问题（1）有唯一解.

3 举例

例1 考虑如下边值问题

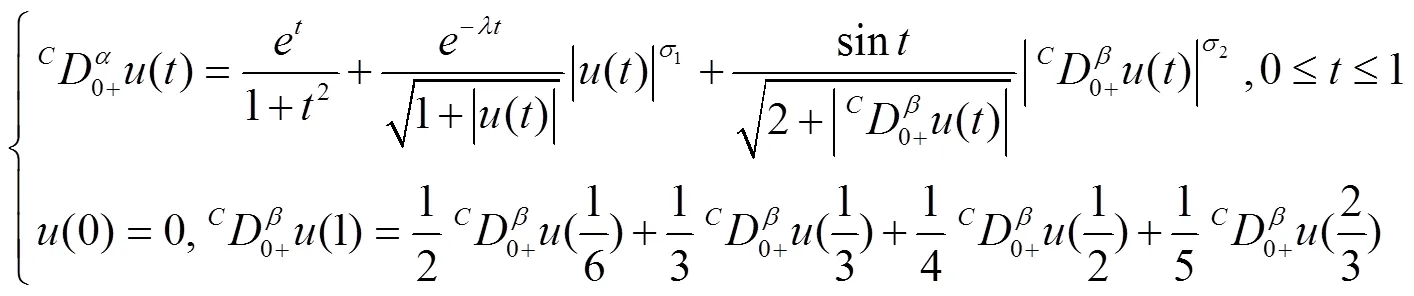
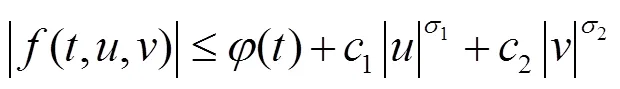
例2 考虑如下边值问题

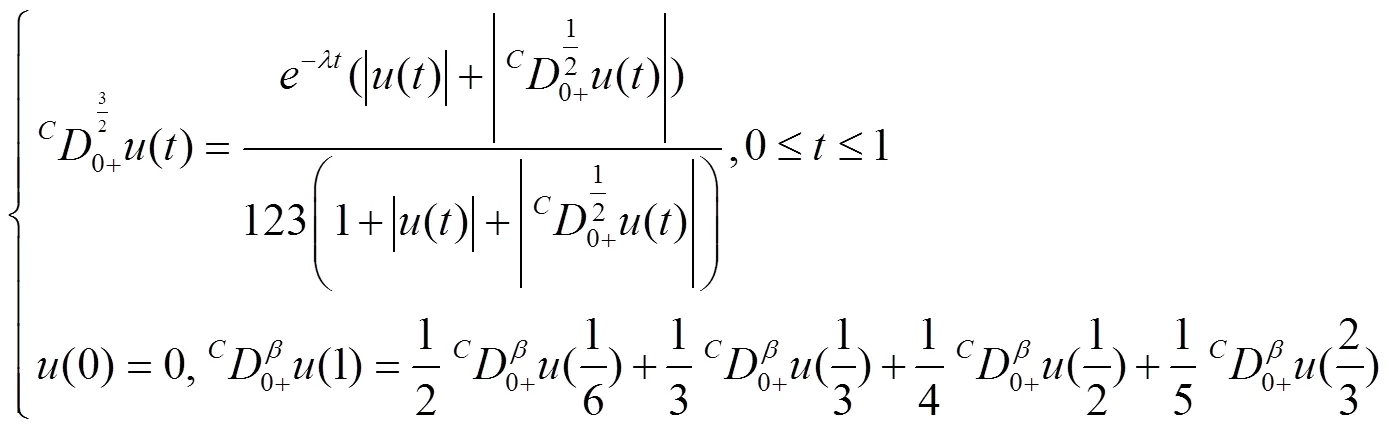
显然式（6）满足定理2的条件，于是有

由定理2，边值问题（5）有唯一解.

[1]葛渭高. 非线性常微分方程边值问题[M]. 北京：科学出版社，2007.

[2]KILBAS A A, SRIVASTAVA H M, TRUJILLO J J. Theory and applications of fractional differential equations[M]. Amsterdam: Elsevier Science B V, 2006.

[3]朱彦，李鑫. 一类非线性分数阶微分方程三点边值问题的解[J]. 黑龙江科技学院学报，2012, 22: 93-97.

[4]许晓婕，孙新国，吕炜. 非线性分数阶微分方程边值问题正解的存在性[J]. 数学物理学报，2011, 31: 401-409.

[5] BAI Zhanbing. On positive solutions of a nonlocal fractional boundary value problem[J]. Nonlinear Analysis, 2010, 72: 916-924.

[6] REHMAN MU, KHAN R A. Existence and uniqueness of solutions for multi-point boundary value problems for fractional differential equations[J]. Applied Mathematics Letters, 2010, 23: 1038-1044.

[7]BAI Zhanbing, ZHANG Yinghan. The existence of solutions for a factional multi-point boundary value problem[J]. Applied Mathematics and Computation, 2010, 60: 2364-2372.

[8]EL-SHAHED M, NIETO J J. Nontrivial solutions for a nonlinear multi-point boundary value problem of fractional order[J]. Computers and Mathematics with Applications, 2010, 59: 3438-3443.

Existence and Uniqueness of Solutions for a Class of Multi-point Boundary Value Problems in Fractional Differential Equations

WUTing, GUChang-chao

(School of Mathematical Sciences, Anhui University, Hefei 230039, China)

The paper is concerned with the existence and uniqueness of solutions for a class of multi-point boundary value problems of fractional differential equations by the use of the Schauder fixed point theorem and the contraction mapping principle. Two examples are given to illustrate the results at the end.

Caputo derivative; boundary value problem; Green function; fixed point theorem; existence; uniqueness

1006-7302（2012）03-0028-07

O175.8

A

2012-03-12

教育部博士点基金资助项目（20113401110001）.

吴婷（1988—），女，安徽省安庆人，在读硕士生，研究方向为微分方程.