带分布型时滞的分数阶控制系统能观性的条件

朱彦



带分布型时滞的分数阶控制系统能观性的条件

朱彦

（安徽大学 数学科学学院，安徽 合肥 230039）

通过Mittag-Leffler矩阵函数构造的能观性Gram矩阵和Cayley-Hamilton定理获得了一类带Caputo导数、具有分布型时滞的分数阶控制系统

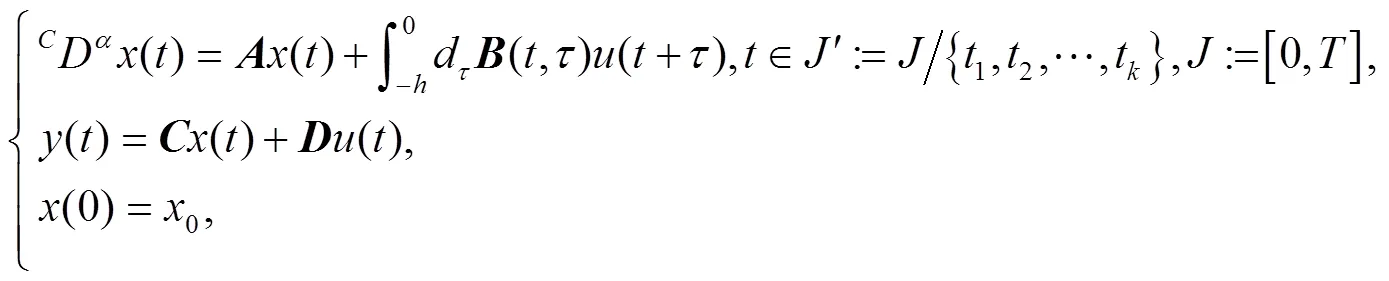
分数阶控制系统；Caputo导数；分布型时滞；能观性；格拉姆矩阵

由于实际控制系统大多是非整数阶控制系统且普遍存在着时滞现象，因此，用带分布型时滞的分数阶模型能较好地模拟实际系统，并得到满意的动态性能和稳定性能. 能控性和能观性分别从控制和观测角度描述了系统的基本特性，它是Kalman在上世纪60年代初首先提出的. 能观性指系统状态的可观测性，它表征了系统的内部状态（通常不可直接测量）被系统输出（通常可直接测量）反映的能力. 近年来，分数阶微积分学及其应用研究正迅猛发展[1-3]，同时分数阶控制系统也吸引了广大学者的研究[4-8]. Balachandran[4]研究了一类带分布型时滞的分数阶控制系统的能控性，本文在此基础上，研究该系统能观性的判断问题.

考虑下面带分布型时滞的分数阶控制系统：

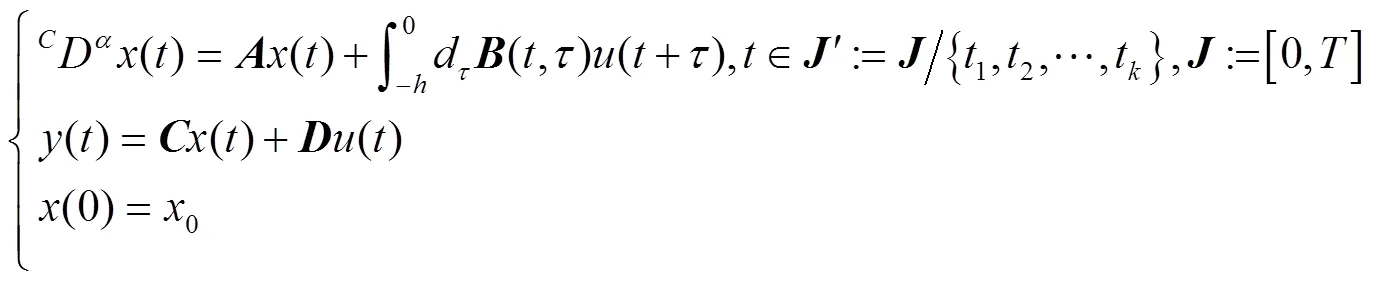
1 预备知识和Green函数

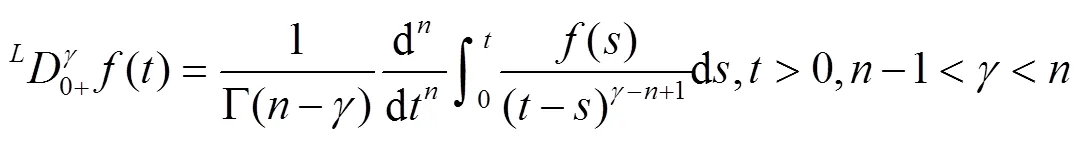
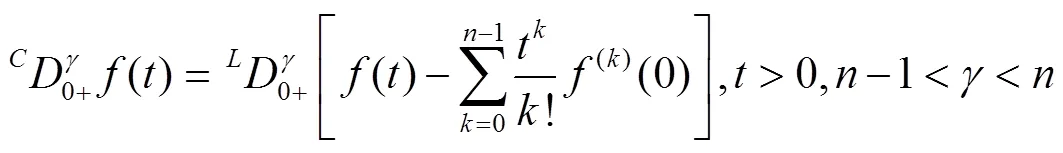
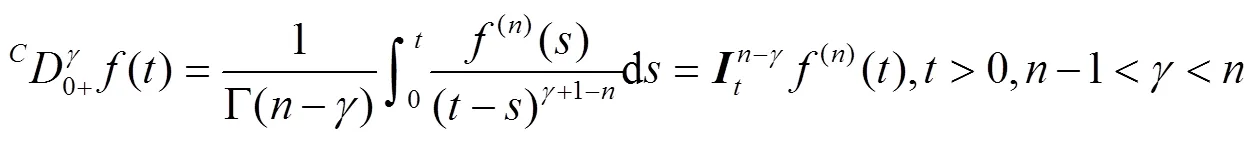
2）常数的Caputo导数恒为0.

定义4 含两参数的Mittag-Leffler函数定义为

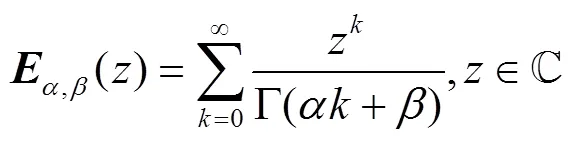
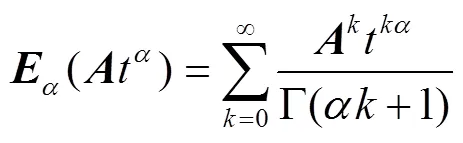
由文献[4]可知，系统（1）的解可以表示为

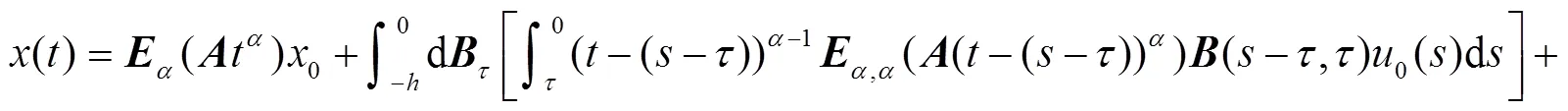
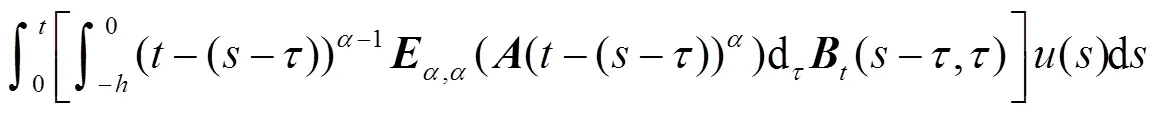
其中

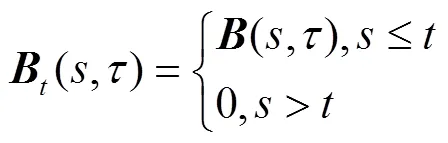
2 能观性的充分必要条件

系统（1）能观性的充分必要条件可记为

.

证明 系统（1）的输入可表示为

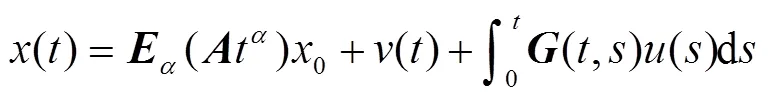
从而控制输出可表示为

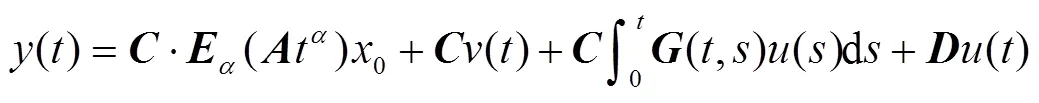
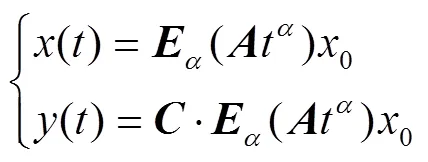
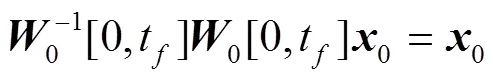
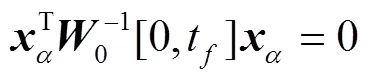
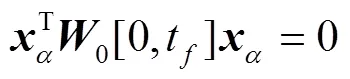
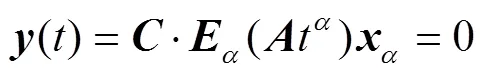
定理2 对于系统（1），构造能观性判别矩阵为

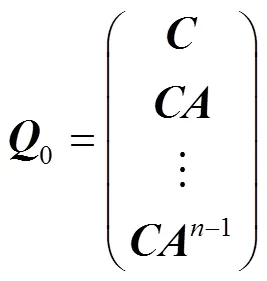
证明 由定理1的证明，得

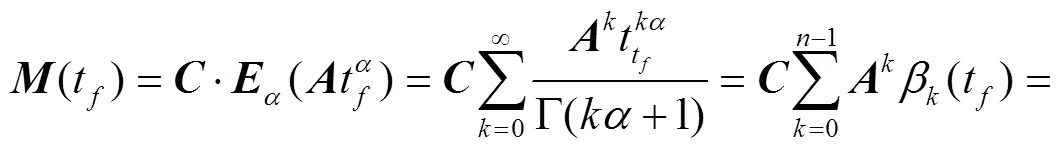
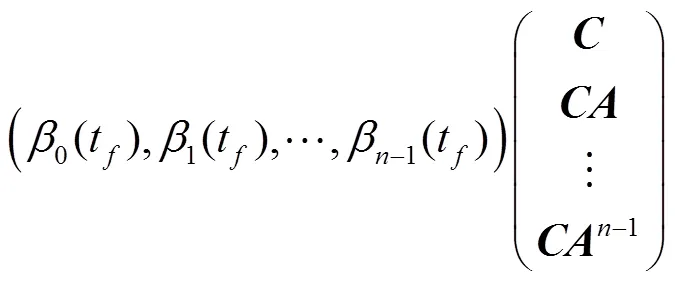
3 举例

例 考虑下列系统的能观性

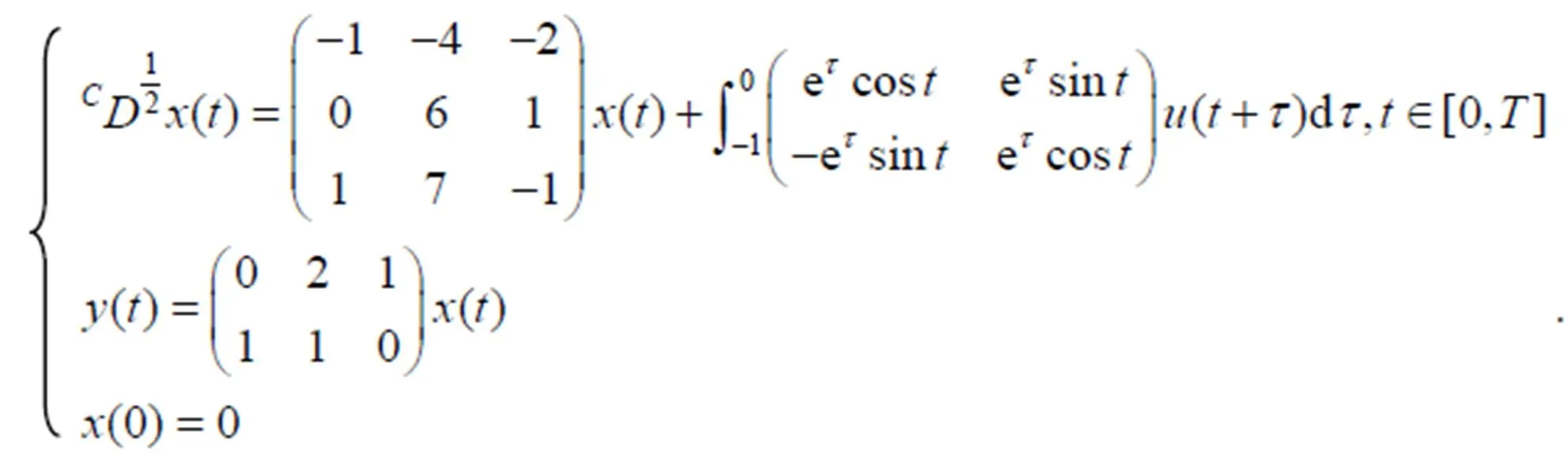
[1] PODLUBNY I. Fractional differential equations[M]//Mathematics in Science and Engineering. New York, London, Toronto: Academic Press, 1999.

[2] LAKSHMIKANTHAM V, BAINOV D D, SIMEONOV P S. Theory of impulsive differential equations[M]. Singapore: World Scientific, 1989.

[3] KILBAS A A, SRIVASTAVA H M, TRUJILLO J J. Theory and applications of fractional differential equations[M]. Amsterdam: Elsevier Science B V, 2006.

[4] BALACHANDRAN K, ZHOU Yong, KOKILA J. Relative controllability of fractional dynamical systems with distributed delays in control[J]. Computers and Mathematics with Applications, 2012. doi: 10. 1016/j. camwa. 2011. 11. 061.

[5] BALACHANDRAN K, PARK J Y, TRUJILLO J J. Controllability of nonlinear fractional dynamical systems[J]. Nonlinear Analysis, 2012, 75: 1919-1926.

[6] GUAN Zhihong, QIAN Tonghui, YU Xinghuo. On controllability and observability for a class of impulsive systems[J]. Systems & Control Letters, 2002, 47: 247-257.

[7] XIE Guangming, WANG Long. Controllability and observability of a class of linear impulsive systems[J]. Mathematical Analysis and Applications, 2005, 304: 336-355.

[8] GUO Tianliang. Controllability and observability of impulsive fractional linear time-invariant system[J]. Computers and Mathematics with Applications, 2012. doi:10. 1016/j. camwa. 2012. 02. 020.

Observability of Fractional Dynamical Systems with Distributed Delays

ZHUYan

(School of Mathematical Sciences, Anhui University, Hefei 230039, China)

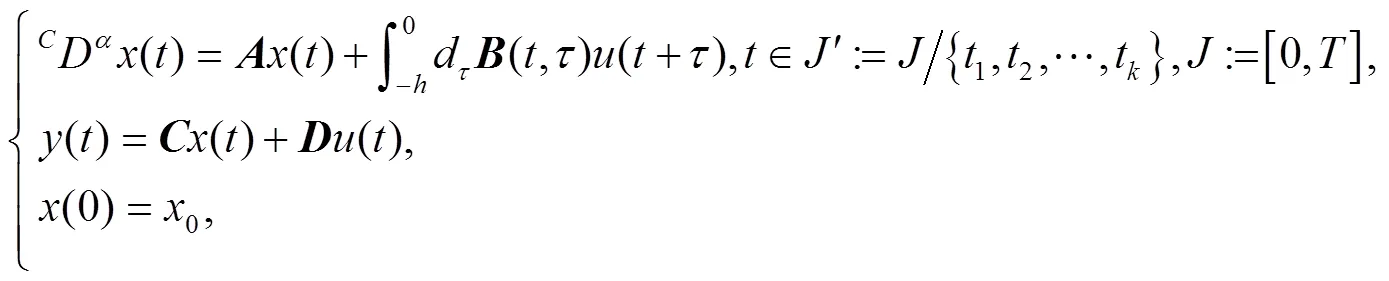
fractional order control system; Caputo derivatives; distributed delays; observability; Gram matrix

1006-7302（2012）03-0023-05

O175. 8

A

2012-03-07

教育部博士点基金资助项目（20113401110001）

朱彦（1988—），女，江苏省泰州人，在读硕士生，研究方向为微分方程.