超立方体网络的限制边连通性

刘芳，欧见平



超立方体网络的限制边连通性

刘芳，欧见平

（五邑大学 数学与计算机科学学院，广东 江门 529020）

超立方体；限制边连通度；网络可靠性

1 超立方体的分解

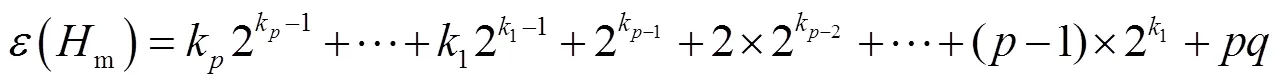
用和分别表示由的点集对所有的和对所有的所导出的子图. 当为偶数时，这两个子图都同构于图，即；当为奇数时，. 不难看出，当为偶数时，和之间存在一个完美匹配；同样的，当为奇数时，和之间也存在一个完美匹配. 这两种情况如图1描述.

证明 由公式（1）可以得出

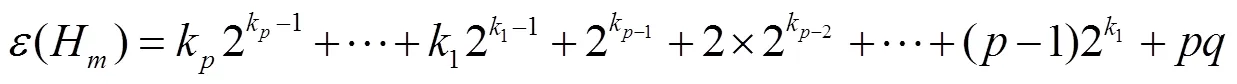
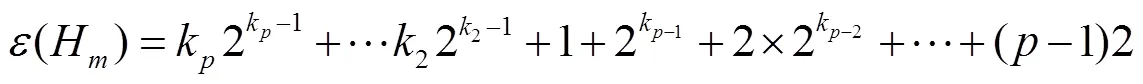
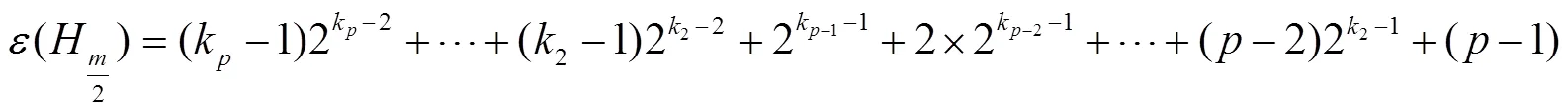
所以，引理成立.

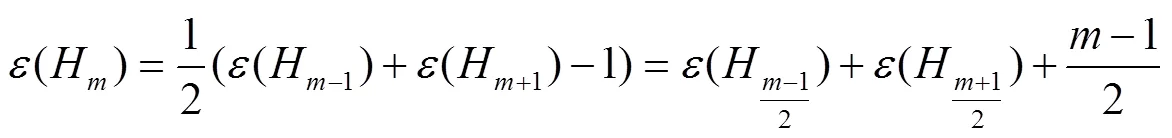
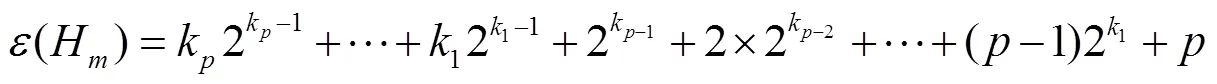
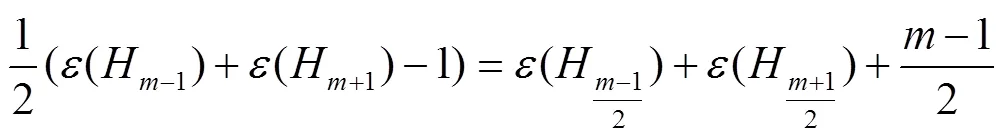
引理得证.

.

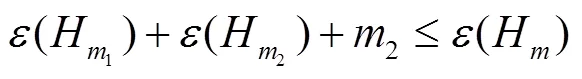
2）如果为奇数、为偶数，由引理2和3得到：

.

3）如果和均为偶数，由引理2和3得到

.

4）如果为偶数、为奇数，那么

.

综上所述，引理成立.

引理5 如果是超立方体中一个顶点数为的子图，那么.

证明 当时结论是成立的，证明省略. 当时，令表示由中的顶点集导出的子图；表示由中的顶点集导出的子图. 则存在正整数，使得. 令，不失一般性假设. 设表示端点分别在和中的边构成的集合. 注意到且，由引理4对进行归纳证明可得：

.

因此，引理成立.

2 限制边连通度

由公式（1）和引理5易得引理6，证明省略.

引理6 如果有，那么.

.

因此，引理成立.

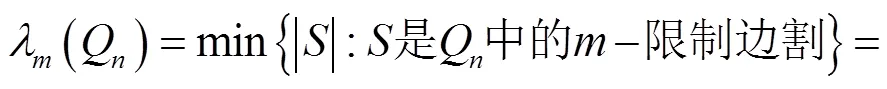
定理成立.

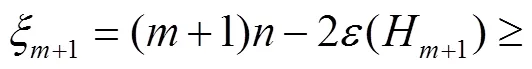
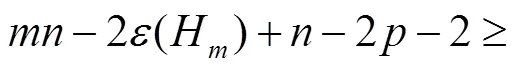
[1]BONSMA P, UEFFING N, BOLKMNN L. Edge-cuts leaving components of order at least three[J]. Discrete Math, 2002, 256:431-439.

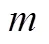
[3]HAJIAGHAYI M T, HAJIAGHAYI M. A note the bounded fragmentation property and its application in network reliability[J]. European J Combin, 2003, 24: 891-896.

[4]HELLWIG A, BOLKMANN L. Maximally edge-connected and vertex-connected graphs and digraphs[J]. Discrete Math, 2008, 308:3265-3296.

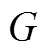
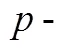
[7] OU Jianping. On optimizing edge connectivity of product graphs[J]. Discrete Math, 2011, 311: 478-492.

[8]WANG Ming, LI Qiao. Conditional edge connectivity properties, reliability comparison and transitivity of graphs[J]. Discrete Math, 2002, 258: 205-214.

[9] OU Jianping, ZHANG Fuji. 3-restricted edge connectivity of vertex transitive graphs [J]. Ars Combin, 2005, 74: 291-302.

[10] BONDY J A, MURTY U S R. Graph theory with applications[M]. New York: Elserier, 1976.

Restricted Edge Connectivity of Hypercube Networks

LIUFang, OUJian-ping

(School of Mathematics and Computation Science, Wuyi University, Jiangmen 529020, China)

hypercube; restricted edge connectivity; network reliability

1006-7302（2012）03-0001-05

O157.5

A

2012-05-14

国家自然科学基金资助项目（11126326）

刘芳（1985—），女，山东济宁人，在读硕士生，研究方向为图论及其应用. 欧见平，教授，博士，硕士生导师，通信作者，研究方向为图论及其应用、网络的可靠性与容错性、化学图论、图的连通性理论.