矩阵方程AXB+CYD=E的Toeplitz矩阵解

孙庆娟，郭文彬，王柄中

(聊城大学数学科学学院，山东聊城252059)

0 前言

矩阵方程是数值代数的重要研究领域。关于矩阵方程

的研究取得了不少进展。例如，1987年，文献［1］利用广义奇异值分解(GSVD)给出了矩阵方程(1)的极小范数解;1998年，文献［2］利用标准相关分解(CCD)研究了该矩阵方程的最小二乘解;2006年，文献［3］利用广义奇异值分解(GSVD)和标准相关分解(CCD)研究了该矩阵方程的极小范数最小二乘解;2007年，文献［4］利用Moore-Penrose广义逆给出了该矩阵方程的对称极小范数最小二乘解;2008年，文献［5］利用矩阵的Kronecker积与广义逆讨论了该矩阵方程的矩阵极小范数对称解，并给出了解存在的充分必要条件及解的表达式;2010年，文献［6］利用构造迭代算法讨论了该矩阵方程的对称最小范数最小二乘解。

然而，文献［1－8］中的方法用于解决矩阵方程(1)的Toeplitz矩阵解有一定的困难。因此，本文将利用Kronecker积、矩阵的拉直算子、Moore-Penrose广义逆来研究矩阵方程(1)的Toeplitz矩阵解和对称Toeplitz矩阵解的表达式，及其最小二乘解的一般形式。

1 基本定义

本文用ℝm×n表示全体m×n阶实矩阵的集合，In表示n阶单位矩阵集合。对于任意矩阵A，B∈ℝm×n，定义A与B的内积〈A，B〉=tr(BTA)，则由此内积所诱导出的范数是矩阵A的Frobenius范数。

定义 1［9］对于 n 阶方阵 X=(xij)∈ ℝn×n，存在一组数 x－(n－1)，x－(n－2)，…，x－1，x0，x1，…，xn－2，xn－1使得X的元素满足xij=xj－i(i，j=1，2，…，n)，则称X为Toeplitz矩阵，记作T(x－(n－1)，x－(n－2)，…，x－1，x0，x1，…，xn－2，xn－1)。全体 n 阶 Toeplitz矩阵的集合记作 Tℝn×n。

定义 2 对于 n 阶方阵 X=(xij)∈ ℝn×n，存在一组数 x0，x1，…，xn－2，xn－1使得 X 的元素满足

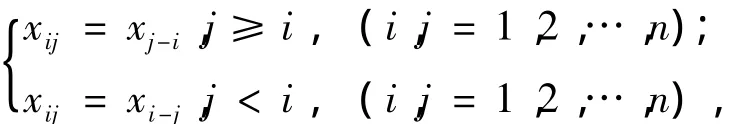
则称 X 为对称 Toeplitz矩阵，记作 ST(x0，x1，…，xn－2，xn－1)。全体 n 阶对称 Toeplitz矩阵的集合记作 STℝn×n。

定义 3［9］设 A ∈ ℝm×n，B ∈ ℝp×q，称 A ⊗ B=(aijB)∈ ℝmp×nq为 A 与 B 的 Kronecker积。

定义 4 设 A=(aij)∈ ℝm×n，记 ai=(a1i，a2i，a3i，…，ami)(i=1，2，3，…，n)，令

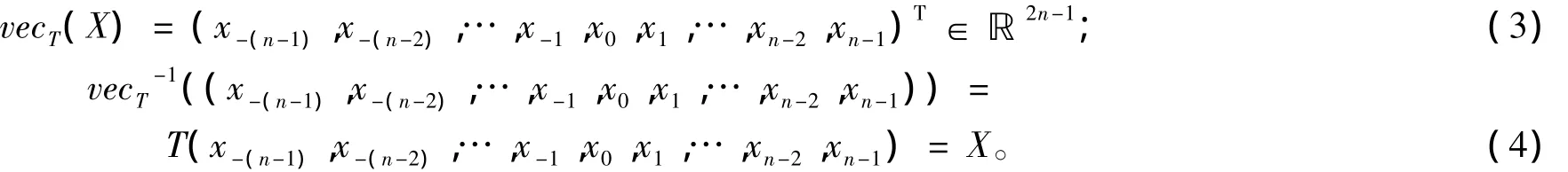
定义 6 当矩阵 X=ST(x0，x1，…，xn－2，xn－1)为 n 阶对称 Toeplitz矩阵时，令

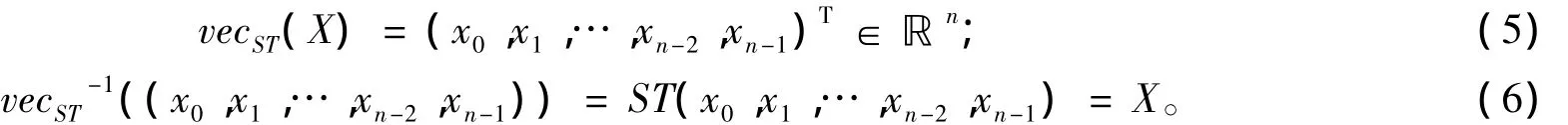
2 矩阵方程AXB+CYD=E的Toeplitz矩阵解

引理 1［9］对于任意的矩阵 A ∈ ℝm×n，B ∈ ℝn×s，C ∈ ℝs×t，总有 vec(ABC)=(CT⊗ A)vec(B)。

引理2 对X∈ℝn×n，则X∈Tℝn×n⇔vec(X)=PnvecT(X)，其中vecT(X)∈ℝ2n－1由式(3)给出，

其中ei为n阶单位矩阵In的第i列。

证明 如果X∈Tℝn×n，则由Toeplitz矩阵的定义可得

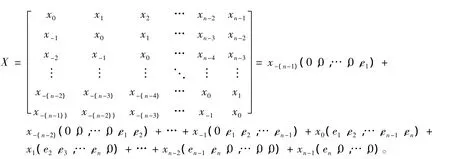
将等式两边拉直有

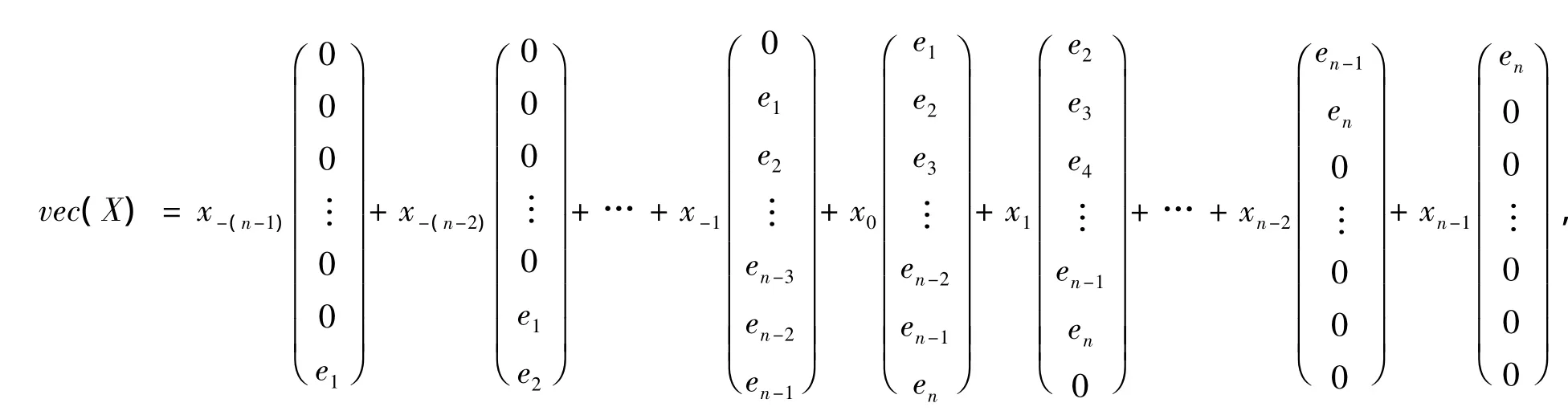
进一步可得

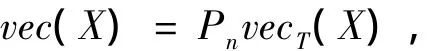
反过来，若 X ∈ ℝn×n且 vec(X)=PnvecT(X)，则可得 X ∈ Tℝn×n。证毕。

引理3［9］设A∈ℝm×n，b∈ℝn，则线性方程组Ax=b有解的充分必要条件为AA+b=b，这时Ax=b的通解是x=A+b+(I－A+A)y，其中y∈ℝn是任意的。

引理4［9］设A∈ℝm×n，b∈ℝn，则不相容线性方程组Ax=b的最小二乘解为x=A+b+(I－A+A)y，其中y∈ℝn是任意的。

下面给出矩阵方程AXB+CYD=E的Toeplitz矩阵解。

定理 1 对给定的 A ∈ ℝm×n，B ∈ ℝn×s，C ∈ ℝm×k，D ∈ ℝk×s，E ∈ ℝm×s，Pn如式(7)所示，

其中，ei为k阶单位矩阵Ik的第i列。vec(X)如式(2)所定义，令W1=(BT⊗A)Pn，W2=(DT⊗C)Pk，则当(W1，W2)+(W1，W2)vec(E)=vec(E)时，矩阵方程(1)的Toeplitz矩阵解可表示为

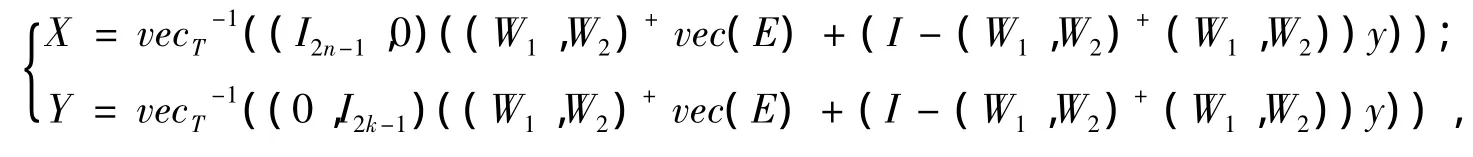
其中y为适当维数的任意向量。

证明 设X、Y分别为矩阵方程(1)的Toeplitz矩阵解，则由引理2知

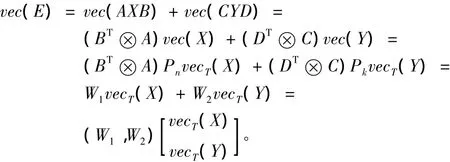
由引理3 知，AXB+CYD=E 有 Toeplitz解当且仅当(W1，W2)+(W1，W2)vec(E)=vec(E)，通解为

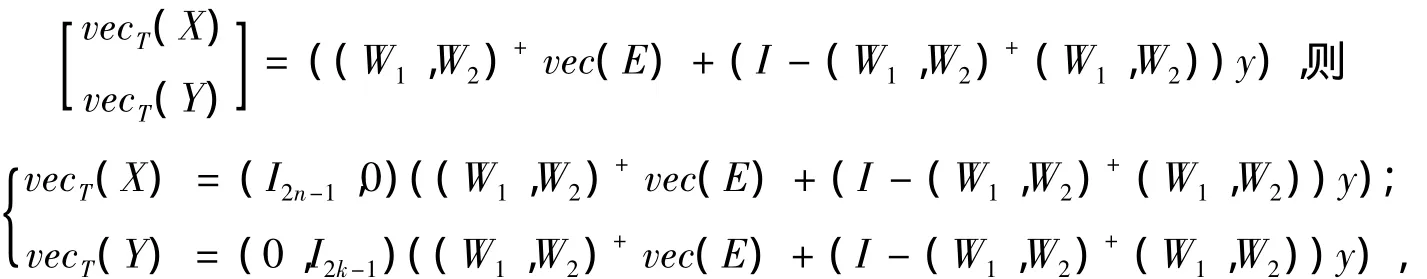
其中y为适当维数的任意向量。

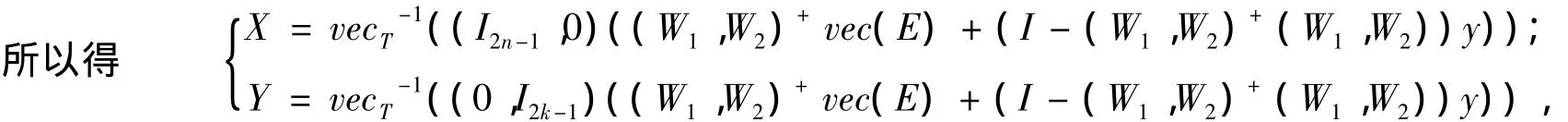
其中y为适当维数的任意向量。证毕。

定理 2 对给定的 A ∈ ℝm×n，B ∈ ℝn×s，C ∈ ℝm×k，D ∈ ℝk×s，E ∈ ℝm×s，Pn如式(7)所示，

其中，ei为k阶单位矩阵Ik的第i列。vec(X)如式(2)所定义，令W1=(BT⊗A)Pn，W2=(DT⊗C)Pk，则当矩阵方程(1)不相容时，满足 AXB+CYD－E=min的最小二乘解的一般形式为

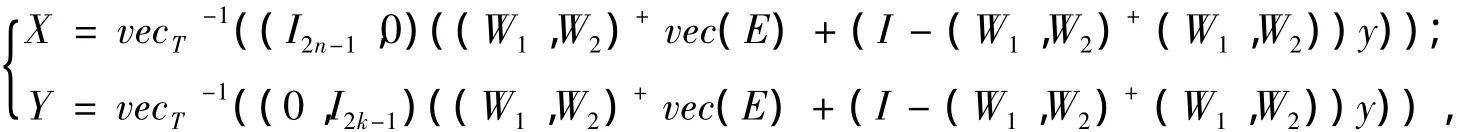
其中y为适当维数的任意向量。

证明 证明与定理1的证明类似，这里省略。

3 矩阵方程AXB+CYD=E的对称Toeplitz矩阵解

引理5 对X∈ℝn×n，则X∈STℝn×n⇔vec(X)=KnvecST(X)，其中vecST(X)∈ℝn由式(5)给出，

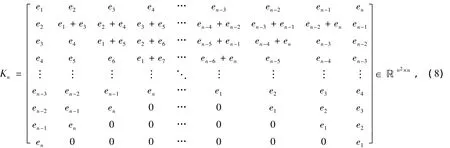
其中ei为n阶单位矩阵In的第i列。

证明 证明与引理2的证明类似，这里省略。

定理 3 对给定的 A ∈ ℝm×n，B ∈ ℝn×s，C ∈ ℝm×k，D ∈ ℝk×s，E ∈ ℝm×s，Kn如式(8)所示，

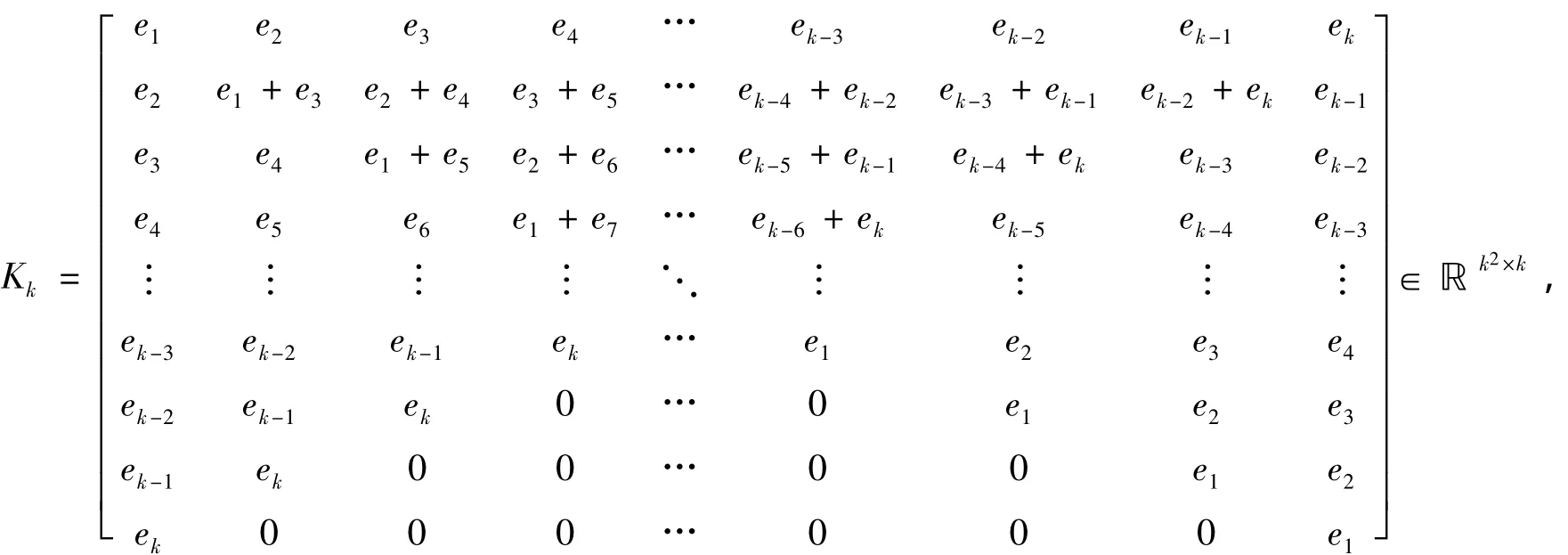
其中，ei为k阶单位矩阵Ik的第i列。vec(X)如式(2)所定义，令U1=(BT⊗A)Kn，U2=(DT⊗C)Kk，则当(U1，U2)+(U1，U2)vec(E)=vec(E)时，矩阵方程(1)的对称Toeplitz矩阵解可表示为

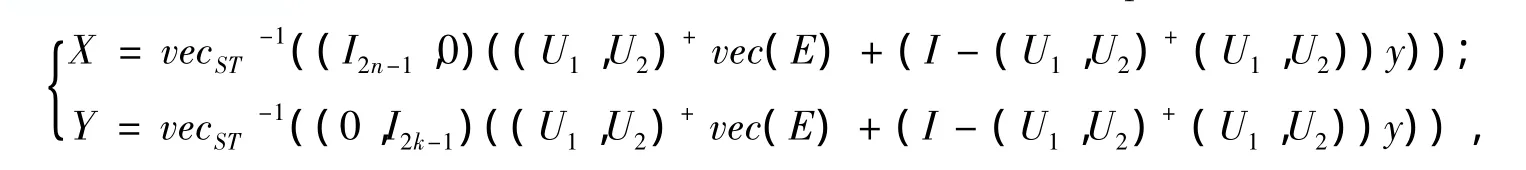
其中y为适当维数的任意向量。

定理 4 对给定的 A ∈ ℝm×n，B ∈ ℝn×s，C ∈ ℝm×k，D ∈ ℝk×s，E ∈ ℝm×s，Kn如式(8)所示，

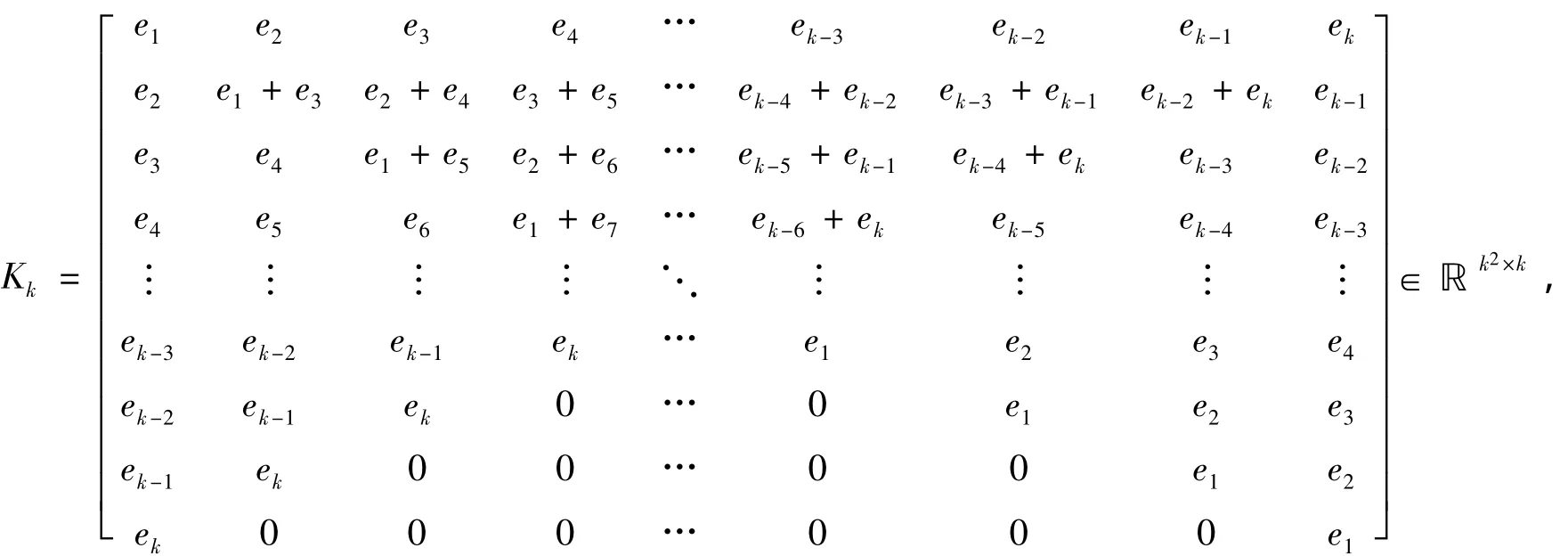
其中，ei为k阶单位矩阵Ik的第i列。vec(X)如式(1)所定义，令U1=(BT⊗A)Kn，U2=(DT⊗C)Kk，则当矩阵方程(1)不相容时，满足 AXB+CYD－E=min的最小二乘解的一般形式为

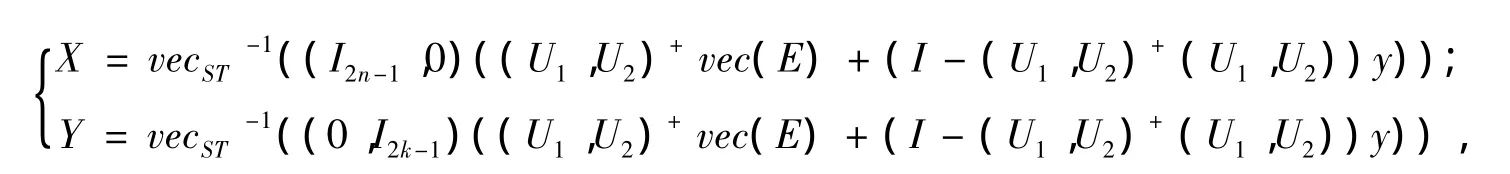
其中y为适当维数的任意向量。

［1］Chu K E.Singular Value and Generalized Singular Value Decompositions and the Solution of Linear Matrix Equations［J］.Linear Algebra Appl，1987，88:83 －98.

［2］Xu G P，Wei M S，Zheng D S.On Solutions of Matrix Equation AXB+CYD=F［J］.Linear Algebra Appl，1998，279:93 －109.

［3］Liao A P，Bai Z Z，Lei Y.Best Approximate Solution of Matrix Equation AXB+CYD=E［J］.SIAM J Matrix Anal Appl，2006，27(3):675 －688.

［4］袁仕芳，廖安平，雷渊.矩阵方程AXB+CYD=E的对称极小范数最小二乘解［J］.计算数学，2007，29(3):203－216.

［5］蒋家尚，袁永新.Symmetric Solutions of the Matrix Equation AXB+CYD=E［J］.南京大学学报:数学半年刊，2008，25(2):141－148.

［6］方玲，廖安平，雷渊.矩阵方程AXB+CYD=E对称最小范数最小二乘解的极小残差法［J］.高等学校计算数学学报，2010，32(1):71 －81.

［7］任俊艳，任颜波，郑华杰，等.交换环上矩阵的加权Moore-Penrose逆与其加边矩阵［J］.河南科技大学学报:自然科学版，2011，32(1):79 －81.

［8］任俊艳，赵丽英.环上矩阵的加权Moore-Penrose逆［J］.河南科技大学学报:自然科学版，2009，30(2):78－81.

［9］戴华.矩阵论［M］.北京:科学出版社，2001.