电势降落对DNA分子器件电荷输运的影响

康大伟，孙孟乐，尤景汉，姬江涛

(1.河南科技大学a.物理与工程学院;b.车辆与动力工程学院，河南 洛阳471003;2.洛阳理工学院 数理部，河南 洛阳471023)

0 前言

随着器件小型化和电路高集成度的发展，传统的集成电路将走到其物理极限。为了克服这一难题，一门新的多领域交叉学科——分子电子学应运而生。分子电子学是利用组装和合成工艺直接从分子尺度上“从下到上”的设计电路。脱氧核糖核酸(DNA)作为一种生物大分子，由于其独有的自组装和自识别特性，特别适合分子电子学的要求，DNA分子中的电荷输运性质已经成为生命科学、化学、物理学等多个交叉学科的研究热点。随着纳米技术的发展，近年来有很多实验直接将单个或一束DNA分子连接到金属电极间，来测量它的电导。这些实验可以更直接的揭示DNA的导电性质，也为DNA作为分子器件的可能性进行了直接的实验验证［1］。这类实验的结果比较复杂，揭示DNA分子可能是绝缘体、半导体、导体甚至超导体［2－7］。导电性的多样结果一是源于DNA本身的性质，DNA的多种序列和分子形态;二是来源于外界环境的影响:温度，溶液中的离子，电极与DNA分子的接触［8－11］。在直接测量实验中，金属电极与DNA分子界面处的良好接触是实验可重复性的一个重要因素，因此有必要研究界面的影响。DNA分子与电极间的连接是实验结果可重复性的一个关键因素，降低界面处的接触电阻是提高器件导电特性的一个有效途径。最近的实验中［12］，DNA分子器件中出现了负微分电导现象，实验结果发现通过DNA分子的电流随着电压的升高反而出现了下降的趋势。在以前的研究中，往往假设电势全部降落在DNA分子与电极的界面处，而在DNA分子上电势降落为零。如果考虑DNA分子上有电势降落，负微分电导的出现是否与界面处的电势降落有关需要进一步的研究。本文拟采用格林函数方法和Landauer-Büttiker公式来研究不同的界面电势降落情况下DNA分子器件中的电荷输运性质。

1 模型和方法

对于金属电极连接的DNA分子器件(见图1)，选取1个螺旋周期(包含11个基对)的Poly(G)-Poly(C)DNA分子。整个体系的哈密顿可以用下式来表示

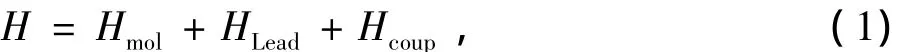
其中Hmol描述了Poly(G)-Poly(C)DNA分子的π轨道。

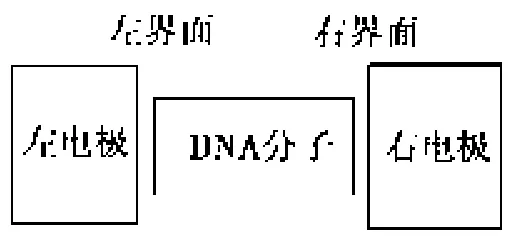
图1 DNA分子器件示意图

金属电极的哈密顿由下式给出

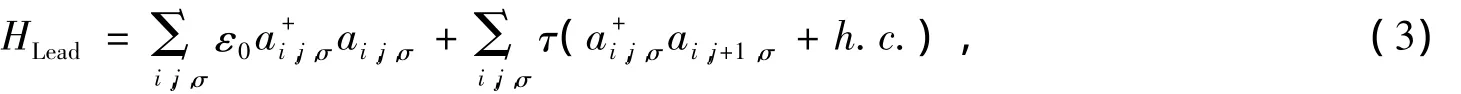
其中，ε0和 τ分别是电极的在位能和相邻格点的跃迁积分是电极中在格点(i，j)位置上产生或消灭一个自旋为σ的电子的算符。

Hcoup描述了电极与DNA分子间的耦合，这个耦合只发生在金属电极和DNA分子的接触界面上

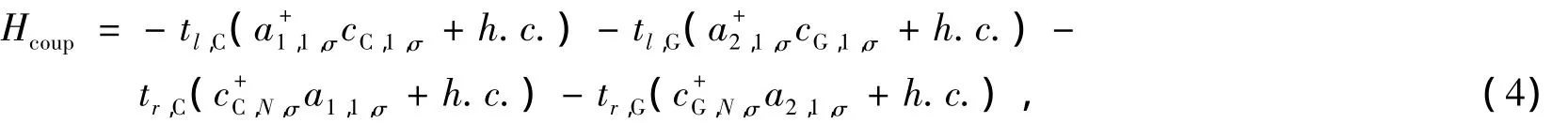
其中假定界面耦合是自旋非相关的。

通过体系的电流就可以通过Landauer-Buttiker公式给出，

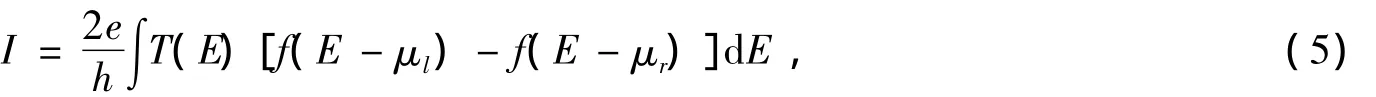
其中，h是普朗克常数;T(E)是电子从左电极到右电极的透射系数

是电极中的费米分布函数，其中μl(r)是左(右)电极的化学势，kB是玻耳兹曼常数，T是温度。透射系数T(E)可以通过Fisher-Lee关系从体系的晶格格林函数得出，

其中I是单位矩阵算符。

本文中参数的选取如下:对于Poly(G)-Poly(C)DNA分子，将其最低占据能级(LUMO)设为在位能:εG=1.14 eV，εC=－1.06 eV。一条链上相邻碱基间的跃迁积分设为tG(C)=0.45 eV，链间的互补碱基间的跃迁积分设为t⊥=0.60 eV，这些都是在参数选取的合理区间。金属电极参数的选取为:τ=1.50 eV。电极的费米面选在DNA带隙的中间。界面耦合设为自旋非相关的，取值为0.40 eV。本文选取的温度为室温T=300 K。

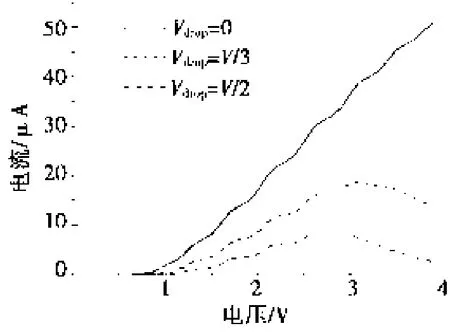
图2 DNA分子器件在不同的电势降落下的电压电流曲线

2 结果与讨论

在金属电极连接的DNA分子器件电荷输运性质的直接实验测量中，分子与电极间良好的界面接触是实验数据可重复性测量的必要条件。当DNA分子与金属电极形成良好的接触后，在金属电极施加外加偏压，这时候左右两个电极处在高低两个不同电势下。在以往的研究中，往往假设电势对称的降落在DNA分子与金属电极的界面处，具体情况为左右两个界面处各降落V/2。这种情况下系统的输运性质如图2中所示。当电压比较小时，体系的电流基本为零，此时金属电极的费米面处于DNA分子禁带内，因此没有分子轨道进入导电窗口。当电压大于0.7 V时，电流开始显著增大，对应着DNA分子的导电能级开始进入导电窗口。随着电压的进一步增大，更多的导电分子能级进入导电窗口，这导致电流进一步增大。因此，此时的电压电流曲线呈现出非线性的单调递增的趋势。由电流随着电压的上升趋势可以看出:在某个导电能级进入导电窗口时，电流上升趋势很快;当电极费米面处在两个导电能级间时，电流随着电压的上升趋势较缓。体系通过的电流在电压为4 V时达到了50 μA，此结果与最近的实验［12］符合。

在实际的实验中，如果分子与电极的界面处电势降落小于电极上施加的电压，则有部分电压会降落在DNA分子上。电势降落不只是发生在界面处的情况下，图2的虚线和点划线分别给出了DNA分子中的电势降落达到总电势降的1/3和1/2两种情况下的电压电流曲线。由图2可以看出:DNA分子上的电势降落压制了通过其中的电流。在低电压下，电流将小于无电势降落的情况。而且随着电压的继续升高，当电压大于3 V时电流反而出现了下降的情况，即出现了负微分电导现象。当DNA分子上的总电势降落所占的比重更大时，即电势有一半降在分子上时，电流进一步降低，而且在电压大于2.6 V时就开始出现负微分电导现象。所以在DNA分子上的电势降落越大，体系的电流越小。而在相同的电势降落下，随着电压的升高，都会出现负微分电导现象。对于DNA分子中电压降落Vdrop=V/3这种情况，当电压达到3 V左右时，电流开始随着电压的升高而降低。而当Vdrop=V/2时，当电压达到2.5 V左右时，电流就会随着电压的升高而降低。可见，随着电势降落在DNA分子上的比例的升高，其负微分电导出现的电压值越低。

为了具体分析产生负微分电导的原因，画出了在不同的电势降落下，LUMO能级(最低未占据能级)对应的波函数的形状。如图3a所示，其中纵坐标为波函数的数值，横坐标为DNA分子碱基对应的坐标。当DNA分子中不存在电压降落时，LUMO能级对应的波函数是扩展在整个分子中的，而扩展的分子轨道可以提供较大的电子透射几率，此时通过体系的电流较大。当 DNA分子中存在电势降落时，如图3b所示，LUMO能级对应的波函数局域在DNA分子的右端，局域轨道阻碍了电子的隧穿，从而降低了通过体系的电流。负微分电导的出现可以解释为:随着偏压的增大，DNA分子上的电势降落持续增大，因而各个导电的分子轨道倾向于局域化，这个效应是减少电流的趋势。另一方面，电压增大导致更多的导电通道进入导电窗口，这是电流增加的趋势。当两方面的因素相互达到平衡时，电流随着电压的升高开始出现拐点，当电压继续增大时，分子轨道局域化的效应开始压制更多导电通道进入导电窗口的效应，因此，电流开始随着电压的升高而下降。

如果电压降落在DNA分子上的比例相对于降落在界面处的比例很小时，波函数的局域效应较弱，而随着电压升高更多的导电通道进入导电窗口，这个效应占主要，所以电流随着电压升高会持续上升。在早期的DNA分子器件导电实验中［13－15］，是通过物理吸附将DNA分子与电极连接，DNA分子与金属电极间的连接不是化学连接，所以接触电阻较大。此时，电势将主要降落在界面处。如果界面处接触很好，电压将被迫降落到DNA分子上，当电压降的比例升高到一定程度，就会出现负微分电导的现象。

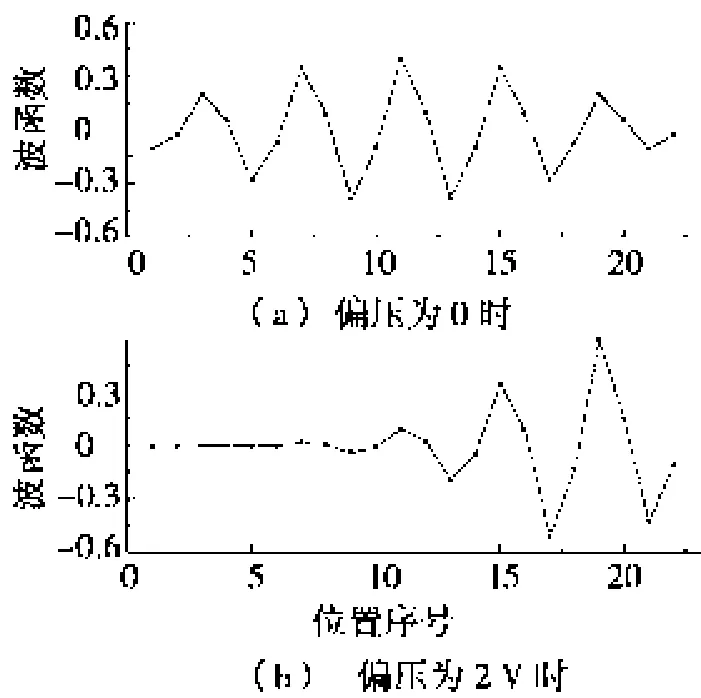
图3 LUMO能级的波函数

3 结论

研究了DNA分子器件中电势降落分布对电荷输运性质的影响。当电势降落全部在界面时，电流随着电压升高是持续上升的;当电势开始降落在DNA分子上时，电流相比DNA分子上没有电势降落的情况会有所降低，而且开始出现负微分电导的现象;当电势降落在DNA分子上的比例进一步提高时，负微分电导出现时对应的电压值更小，而且下降的趋势更明显。分析了产生负微分电导的原因，发现电势降落引起的分子轨道的局域是主要因素，电势降落越大，分子局域现象越明显，这就进一步促使了负微分电导的出现。

［1］Endres R G，Cox D L，Singh R R P.Colloquium:The Quest for High-conductance DNA［J］.Rev Mod Phys，2004，76:195 －214.

［2］Fink H W，Schonenberger C.Electrical Conduction Through DNA Molecules［J］.Nature，1999，398:407 －410.

［3］Porath D，Bezryadin A，Vries S de，et al.Direct Measurement of Electrical Transport Through DNA Molecules［J］.Nature，2000，403:635 －638.

［4］Roy S，Vedala H，Roy A D，et al.Direct Electrical Measurements on Single-molecule Genomic DNA Using Single-walled Carbon Nanotubes［J］.Nano Lett，2008(8):26 － 30.

［5］Song B，Elstner M，Cuniberti G.Anomalous Conductance Response of DNA Wires Under Stretching［J］.Nano Lett，2008(8):3217－3220.

［6］Xu B Q，Zhang P M，Li X L，et al.Direct Conductance Measurement of Single DNA Molecules in Aqueous Solution［J］.Nano Lett，2004(4):1105 －1108.

［7］Yoo K H，Ha D H，Lee J O，et al.Electrical Conduction Through Poly(dA)-Poly(dT)and Poly(dG)-Poly(dC)DNA Molecules［J］.Phys Rev Lett，2001，87(19):198102.

［8］Cuniberti G，Craco L，Porath D，et al.Backbone-induced Semiconducting Behavior in Short DNA Wires［J］.Phys Rev B，2002，65:241314.

［9］Guo A M，Xiong S J.Effects of Contact and Efficient Charge Transport in G4-DNA Molecules［J］.Phys Rev B，2009，80:035115.

［10］Maciá E，Triozon F，Roche S.Contact-dependent Effects and Tunneling Currents in DNA Molecules［J］.Phys Rev B，2005，71:113106.

［11］Wang X F，Chakraborty T.Charge Transfer Via a Two-Strand Superexchange Bridge in DNA［J］.Phys Rev Lett，2006，97:106602.

［12］Ning K，Artur E，Elke S.Observation of Negative Differential Resistance in DNA Molecular Junctions［J］.Appl Phys Lett，2010，96:023701.

［13］Cohen H，Nogues C，Naaman R，et al.Direct Measurement of Electrical Transport Through Single DNA Molecules of Complex Sequence［J］.Proc Nat Acad Sci，2005，102:11589.

［14］Ullien D，Cohen H，Porath D.The Effect of the Number of Parallel DNA Molecules on Electric Charge Transport Through‘Standing DNA’［J］.Nanotechnology，2007，18:424015.

［15］Nogues C，Cohen S R，Daube S，et al.Sequence Dependence of Charge Transport Properties of DNA［J］.J Phys Chem B，2006，110:8910.1a21a1b