模糊PID参数的相平面法整定策略

孙建延，王振成

(中州大学工程技术学院，河南郑州450044)

0 前言

PID控制即比例－积分－微分控制，它是建立在经典控制理论上的一种控制策略，在工业过程中得到广泛应用。常系数PID控制器为线性控制器，将误差的比例、积分、微分通过线性组合构成控制量，对被控对象进行控制，其对大多数单输入单输出线性过程具有令人满意的控制效果，而对于复杂过程却无能为力［1－2］。为了改进PID控制效果，出现了多种改进型PID［3］。变系数PID是其中一种重要的形式，模糊推理为变系数PID系数提供平滑切换的方法。模糊推理与PID结合的模糊PID控制器在实际中得到广泛应用［3－6］。

模糊PID的整定往往采用试凑法，整定过程慢，控制性能无法得到保证。文献［7］将模糊PID的整定分为非线性和线性两级整定，非线性级为模糊规则库的整定，线性级为量化因子的整定。模糊规则库决定了控制器的非线性性能，本文着重介绍了基于相平面法的规则库。根据控制对象的动态响应特征，在相平面划分为不同的区域，将不同区域映射到规则库，由此整定规则库内容［4，8－10］。该整定方法直观，通用，方便实施。

1 模糊PID控制器

图1是模糊PID控制器结构原理图，KP、KI、KD为比例、积分、微分系数，e，△e为误差及误差变化率。其利用模糊推理理论建立参数KP、KI、KD与e，△e之间的模糊逻辑关系，不同的e和△e要有不同的KP、KI、KD与之相对应，以使系统在不同的工作环境达到最优。

模糊PID的离散形式为

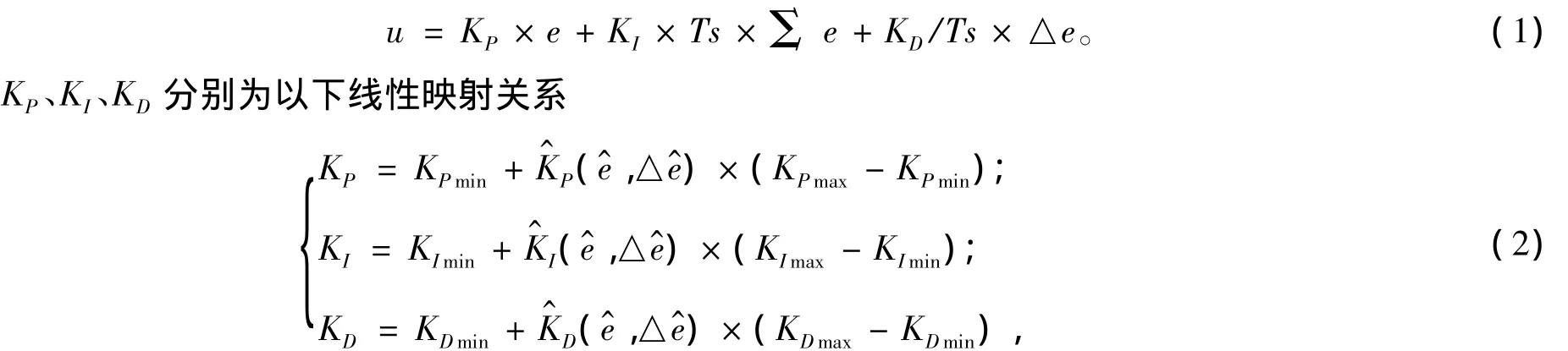
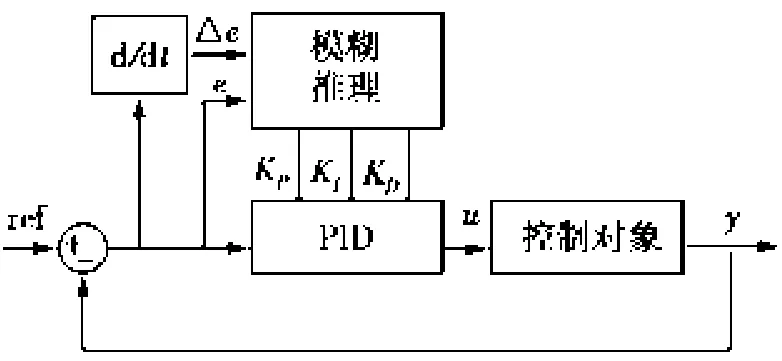
图1 模糊PID控制器参数整定原理图

上述模糊推理过程如果采用带有乘积推理机、单值模糊器、中心平均解模糊器的模糊推理系统，则的解析表达式如式(3)～式(5)所示。其中的隶属度函数，KPij、KIij、KDij为单值模糊器所对应的 KP、KI、KD的模糊值，即模糊 PID 规则库。

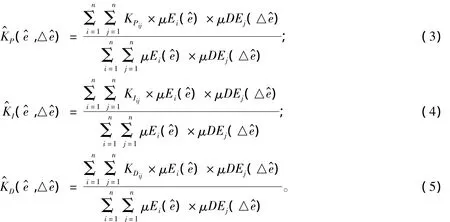
2 非线性级(模糊规则表)的整定

控制对象的典型阶跃响应曲线如图2所示。阶跃响应在相平面上的轨迹如图3所示。根据(e，△e)在相平面上所处的象限，将阶跃响应曲线分为A、B、C、D、E 区语言变量取{NB NS ZE PS PB}，分别表示负大、负小、零、正小、正大，隶属度函数取对称三角函数，中心均匀分布在［－1，1］语言变量取为{B S Z}，分别表示大、小、零，采用单值模糊化，中心分别在［0 0.5 1］，其隶属度函数如图4所示。语言变量将相平面分为5×5的区域，根据动态响应过程又可分为起动区、加速区、制动区和回调区，如图4所示。

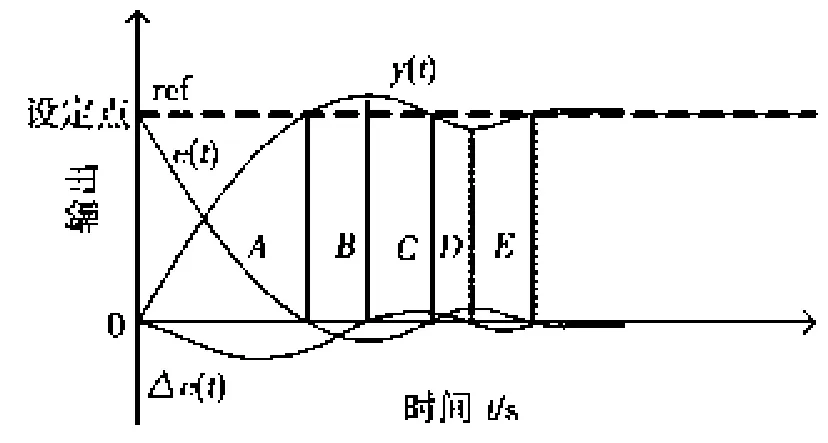
图2 控制对象阶跃响应

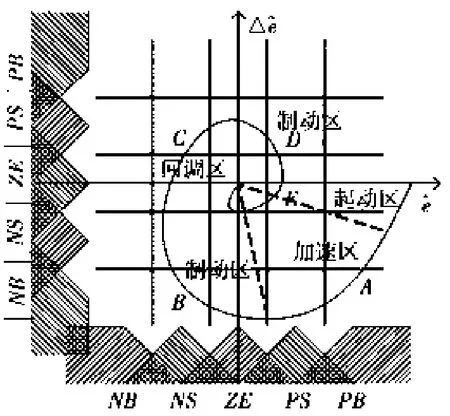
图3 5×5语言相平面及响应轨迹图

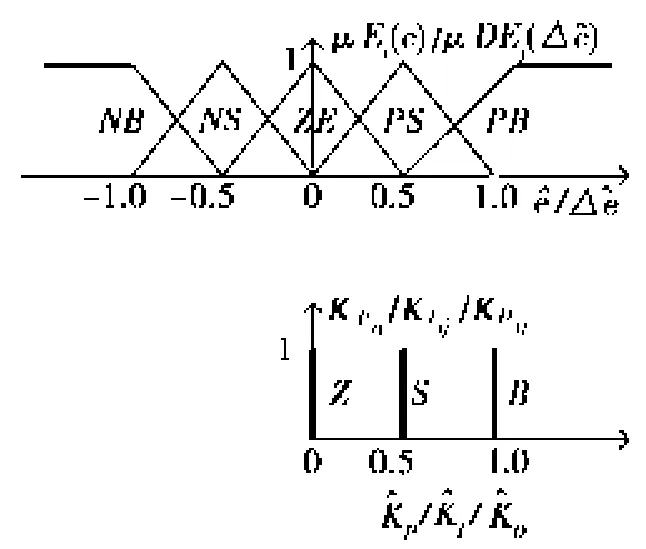
图4隶属度函数

KP、KI、KD的作用分别为:KP越大，系统的响应速度越快，但易产生超调，甚至会导致系统不稳定;KI越大，系统的静态误差消除越快，但KI过大，在响应过程的初期会产生积分饱和现象，从而引起响应过程的较大超调;KD是在响应过程中抑制偏差向任何方，但KD过大，会使响应过程提前制动，从而延长调节时间，而且会降低系统的抗干扰性能。

为使系统阶跃响应较高的动态性能、超调小，并能消除稳态误差，对应于图4相平面，在各个区域分别有:

(Ⅰ)在起动区，为加快系统响应速度，KP系数取B;为防止积分饱和，KI系数取Z;△e为负值，抑制了加速过程，KD系数取Z。

(Ⅱ)在制动区，为防止超调，KP系数取Z;KD系数取B。

(Ⅲ)在加速区，为使PID系数光滑过渡，KP系数取S;KD系数取S。

(Ⅳ)在回调区，为使输出回到参考值，KP取B，KI取B。

(Ⅴ)在稳定区，为降低对噪声的敏感性，KP取S，KD取S;为消除静差增大KI，KI取B。根据性能要求，稳定区应灵活取值，若是“紧控制”，KP取B，KD取B;若是“近似控制”，KP取Z，KD取Z，仅有积分起作用。

(Ⅵ)在右上与右下区域，为(e，△e)轨迹远离给定的方向运动，KP取B，KI取B，KD取B。

由此，制定KP、KI、KD模糊规则表，分别见表1、表2和表3。由表1所对应的曲面如图5所示。e，△e经量化后为e^，△e^，取值限制在［－1，1］，p.u.为标幺值。由表2所对应的曲面如图6所示。将式(1)中积分项改写为Ts×Σ (KI×e)，式(1)具有分离积分的作用。由表3所对应的曲面如图7所示。

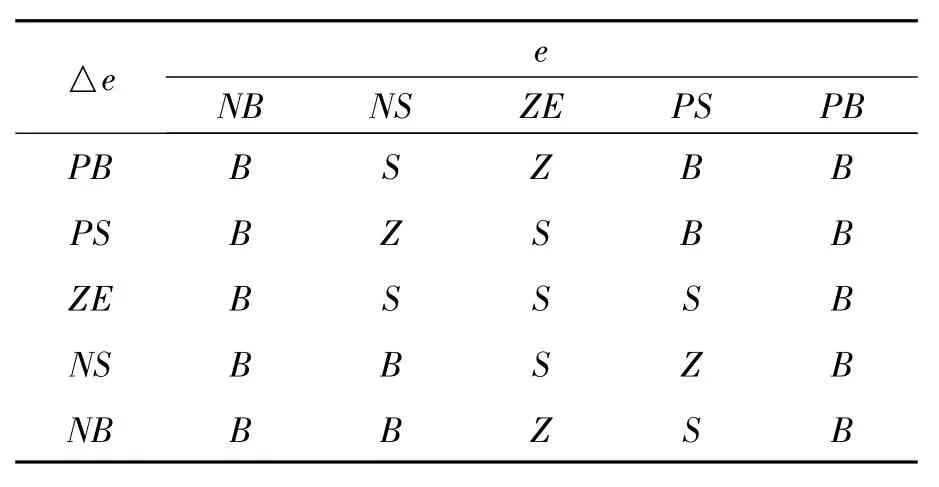
表1 模糊规则表KP

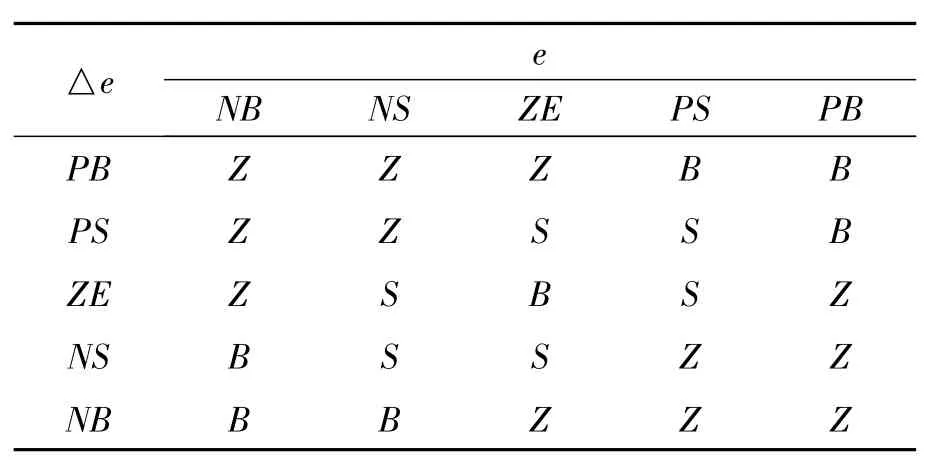
表2 模糊规则表KI

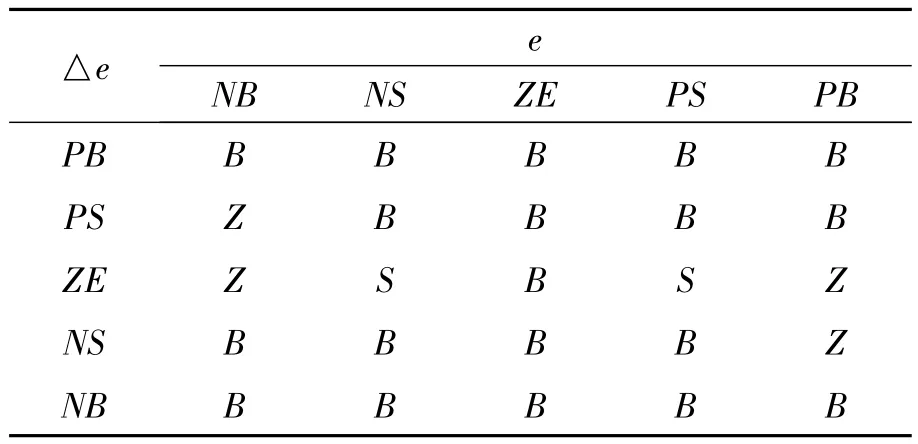
表3 的模糊规则表KD

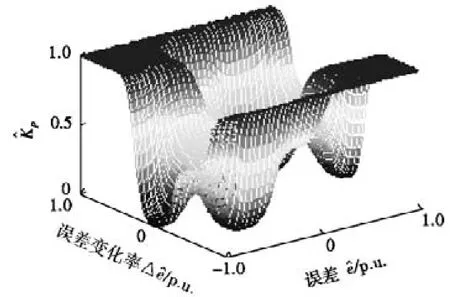
图5 曲面

3 线性级(量化因子)的整定

量化因子的作用是将e，△e量化到图3所设定的区域中，使KP、KI、KD按照预先设定的切换。

对控制对象 P(s)，给定为30，emax=30。超调不超过1，应将量化前e［－1 1］设定在回调区［－0.25 0］内，取量化因子Gc=0.1，e^隶属函数中心对应量化前e为10×［－1 －0.5 0 0.5 1］。

P(s)稳态增益为0.02，控制器输入限幅［－25，25］，采样周期0.2 s，由此得到△emax=25 ×0.02 ×0.2=0.1，设量化因子Gc=10，△隶属函数中心对应量化前△e为0.1×［－1－0.50 0.51］。如果控制对象未知，△emax也可通过试验的方法得到。

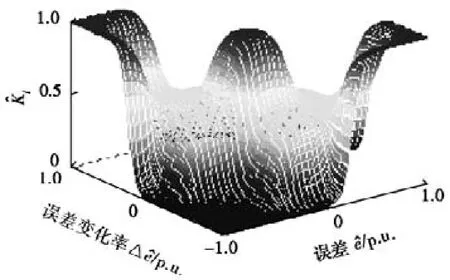
图6 曲面

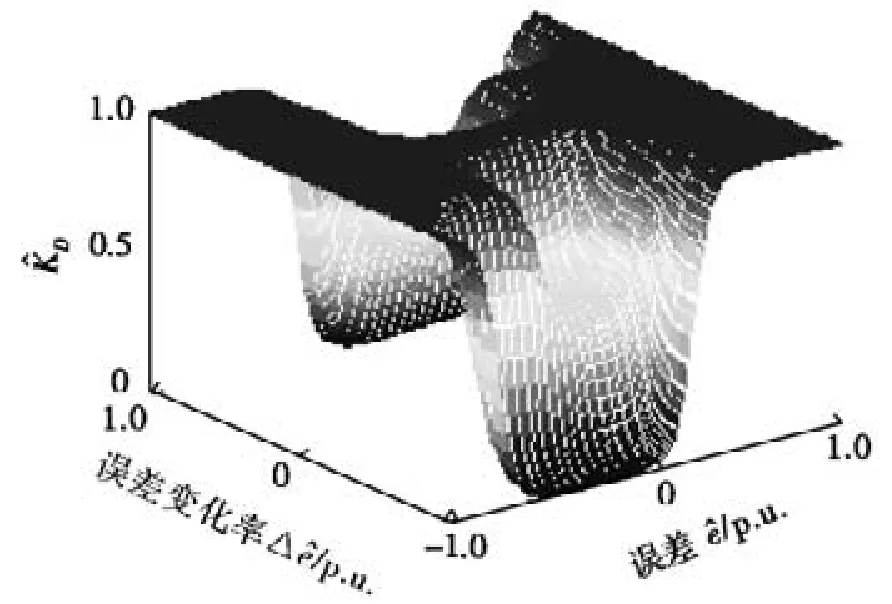
图7 曲面

4 仿真试验结果

通过仿真确定 KP、KI和 KD取值区间分别为 KPmin=0，KPmax=5;KImin=0，KImax=0.005;KDmin=0，KDmax=500。

P(s)阶跃响应如图8所示。模糊PID具有积分项，如果执行器存在死区等非线性环节时，可很快消除静差。P(s)有一个0极点，但积分项的存在并没有引起大幅超调。

由仿真结果(见图9)可知:模糊PID与常系数PID控制器(KP=3，KI=0，KD=500)控制效果相比，超调小，调节时间短。

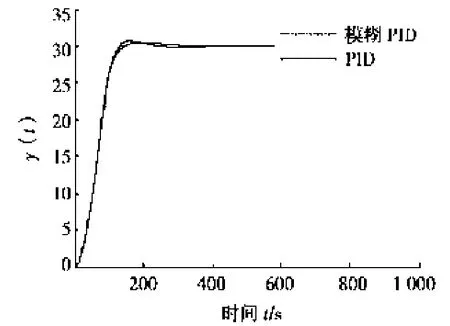
图8 阶跃响应y

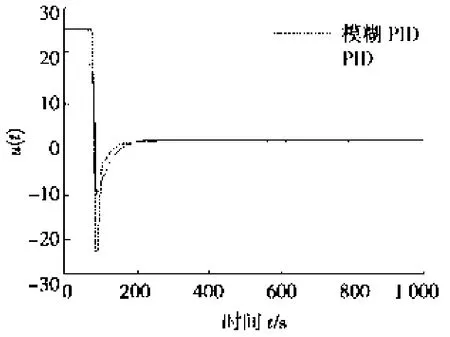
图9 控制器输出u

5 结论

本文分析了在相平面上设计模糊PID规则库的方法，给出了一般性的设计步骤，以相平面为工具克服了模糊PID规则库设计的随意性和盲目性［5－6，9，11－12］。规则库可以根据对象的相平面上表现的动态特征灵活修改，从而正确描述对象的非线性特征。该设计方法直观通用，对模糊PID控制器的整定有较强的指导意义和工程价值。

［1］吴宏鑫，沈少萍.PID控制的应用与理论依据［J］.控制工程，2003，10(1):37－42.

［2］Mohan B M，Sinha A.Analytical Strcture and Stability Analysis of a Fuzzy PID Controller［J］.Applied Soft Computing，2008，8(1):749－758.

［3］刘金锟.先进PID控制MATLAB仿真［M］.北京:电子工业出版社，2004.

［4］张立权.模糊推理系统技术［M］.北京:机械工业出版社，2009.

［5］李强华，张根宝.模糊PID控制在水位控制中的应用与仿真［J］.河南科技大学学报:自然科学版，2006，27(4):49－51.

［6］李水良，杜迎慧，闫守成.电磁离合器电流的模糊自调整PID控制［J］.河南科技大学学报:自然科学版，2010，31(2):43－46.

［7］George K I M，Hu B G，Raymond G G.Two-Level Tuning of Fuzzy PID Controllers［J］.IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics，2001，31(2):263 －269.

［8］胡寿松.自动控制原理［M］.4版.北京:科学出版社，2007.

［9］张吉礼，欧进萍，于达仁.基于相平面轨迹特征的规则自调整模糊控制方法［J］.控制理论与应用，2003，20(4):607－611.

［10］盖晓华，刘叔军.一种新的相平面分区控制器的分析与仿真［J］.计算机仿真，2009，26(7):208－211.

［11］王述彦，师宇，冯忠绪.基于模糊PID控制器的控制方法研究［J］.机械科学与技术，2011，30(1):166－172.

［12］王正林.MATLAB/Simulink与控制系统仿真［M］.2版.北京:电子工业出版社，2008.