广义Ito方程组的对称和新的显式解

张颖元，刘希强，王岗伟

(聊城大学数学科学学院，山东聊城252059)

0 前言

本文将利用修正的CK直接方法研究下述广义Ito方程组［1］

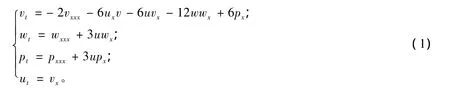
方程组(1)是著名的Ito可积模型的推广，把它称作GIto。利用Hirota双线性方法，文献［2］找到了GIto方程组中p=0时的3孤子解和4孤子解。随后，文献［3］对其可积性进行了研究，发现它们都具有潘勒韦意义下的可积性。在文献［4］中，利用改进的雅克比椭圆函数法得到了方程组(1)的双周期解。文献［5-6］中，找到了方程组(1)的许多行波解。为了求解方程组非线性模型的精确解，已经提出了许多解决的方法。如Backlund变换法和Darboux变换法［7］，截断潘勒韦分析方法［8］，扩展的Riccati方程方法［9］等。本文首先利用修正的CK直接方法，建立了方程组(1)的新、旧解之间的关系，推广了文献［4］中相应的结果，导出了对称群理论。其次，得到了方程组(1)的相似约化和一些新的显示解。最后，给出了相应的结论。

1 GIto方程组的新旧解之间的关系和对称群

假设方程组(1)具有下述形式的对称群

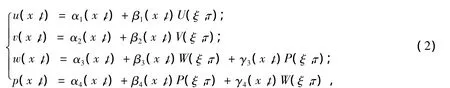
其中，αi、βi(i=1，2，3，4)、γ3、γ4、ξ和 τ 都是关于{x，t}的待定函数，并且在变换{x，t，u，v，w，p}→ {ξ，τ，U，V，W，P}下要求 U(ξ，τ)、V(ξ，τ)、W(ξ，τ)、P(ξ，τ)也满足方程组(1)，即

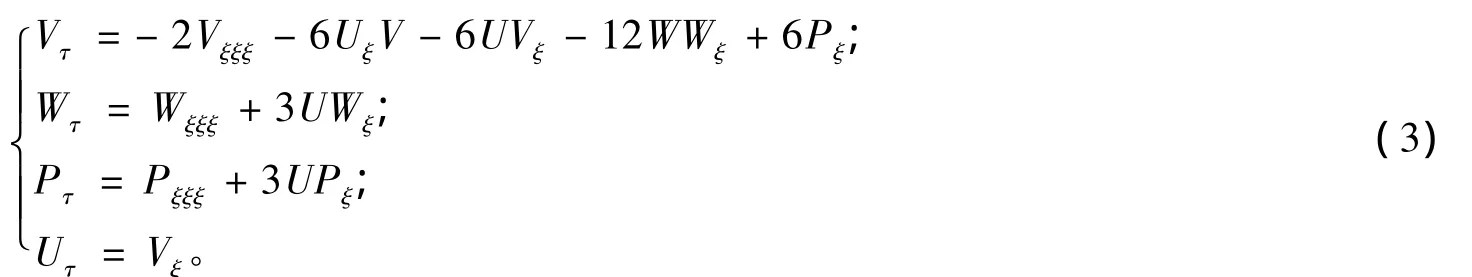
把式(2)代入方程组(1)，并利用约束方程组(3)消去 Uτ、Vτ、Wτ、Pτ，令 U(ξ，τ)、V(ξ，τ)、W(ξ，τ)、P(ξ，τ)和它们的导数项的系数为0，得到下述超定方程组

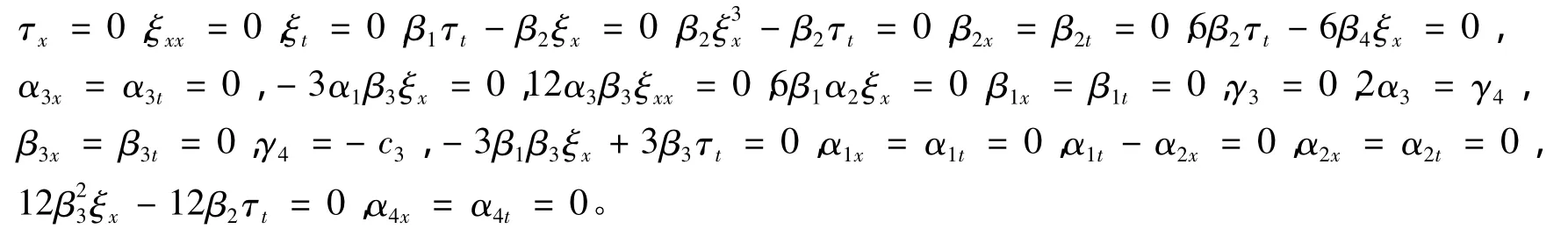
解上述方程组，得到

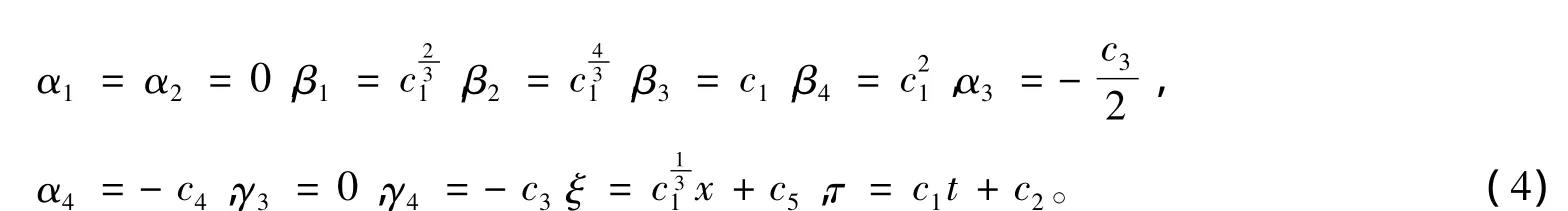
其中，c1、c2、c3、c4和 c5是任意常数。

根据上述过程，对于GIto系统，有下述对称群定理:

定理1 如果 U=U(ξ，τ)，V=V(ξ，τ)，W=W(ξ，τ)，P=P(ξ，τ)是方程组(1)的解，那么下列u、v、w和p也是方程组(1)的解，其中ξ和τ由式(4)决定。

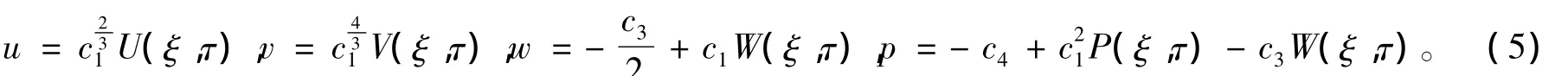
利用定理1，可以推广相应的已知解，从而建立了Ito方程组的新旧解之间的关系。通过文献［4］中的解，可以得到以下椭圆函数解

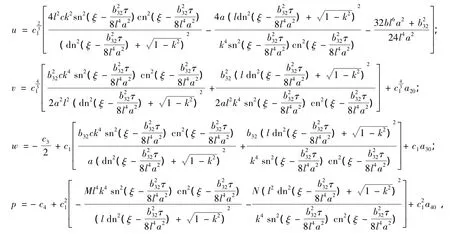
其 中，a、b、c、a20、a30、a40、l 和 b32是 任 意 常 数和τ由式(4)决定。

根据定理1，可以限制c1=1+εc1;c2= εc2;c3= εc3;c4= εc4;c5= εc5，其中，ε 是无穷小参数，并且c1、c2、c3、c4和c5是任意常数，则可以通过以上变换得到方程组(1)的李点对称群。

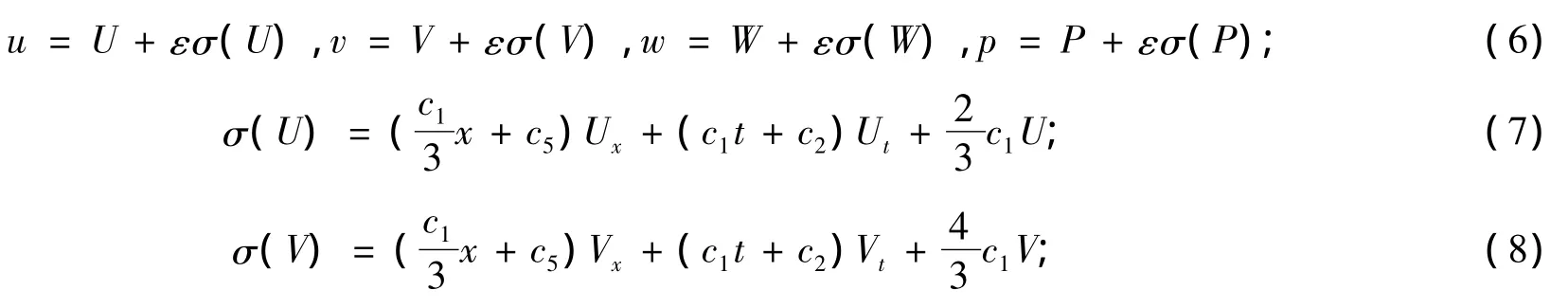
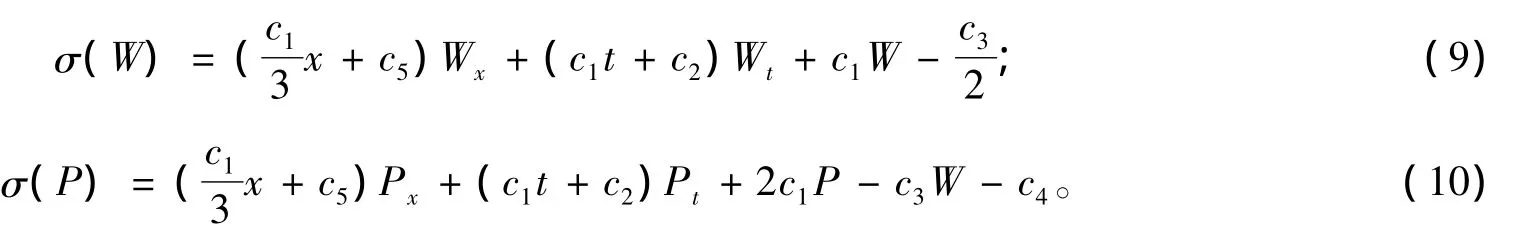
2 GIto方程组的相似约化和显式解

为了求出方程组(1)的相似约化和精确解，根据对称可得下述对应的特征方程组

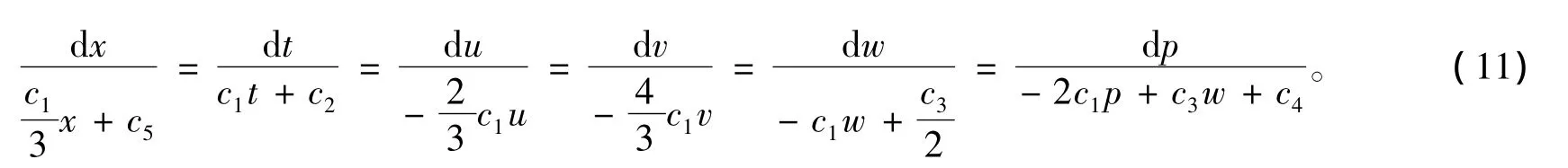
选取下述情况讨论:

情况1 c1=1，c2=c3=c4=c5=0。解相应的特征组可得函数

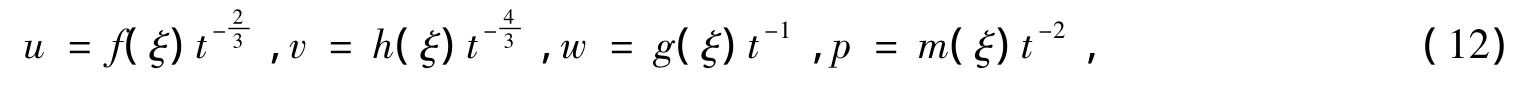
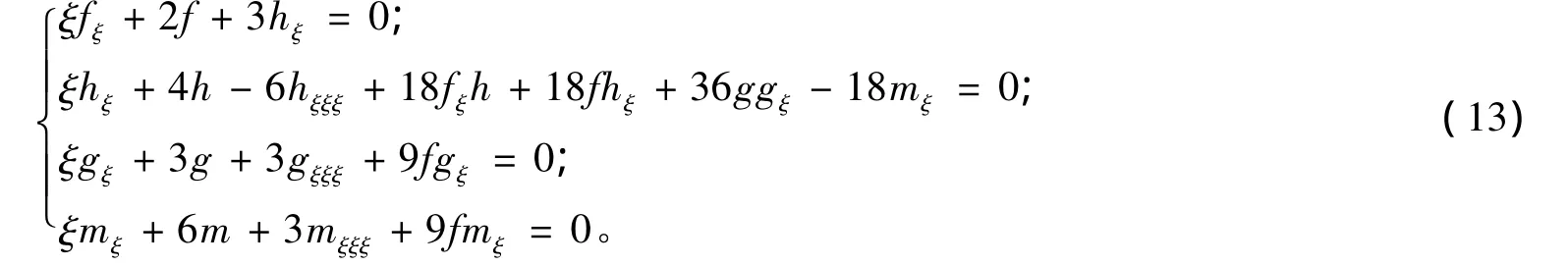
情况2 c1=c2=c4=0，c3=c5=1。解相应的特征方程组，则函数u、v、w和p可以表示为

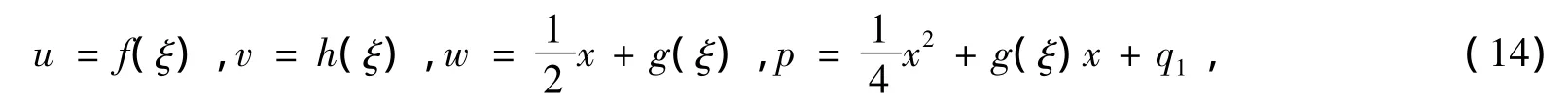
其中，ξ=t;q1是任意常数。函数u，v，w和p可满足下述约化方程

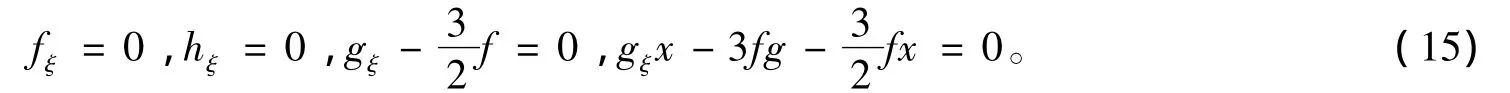
情况3 c1=c3=c4=c5=0，c2=1。可得下述相似变量和函数

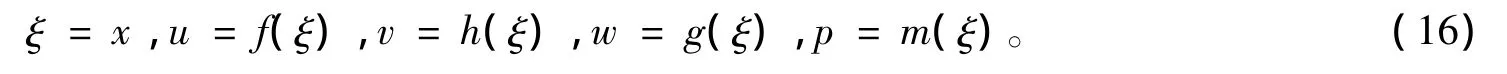
把式(16)代入方程组(1)，可得方程(1)的约化方程为

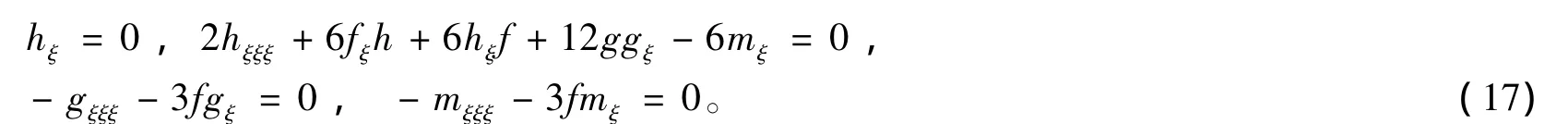
情况4 c2=c5=1，c1=c3=c4=0。可得下述不变量 ξ和函数 u、v、w、p，

把式(18)代入方程组(1)，则方程组(1)的约化方程可以表示为

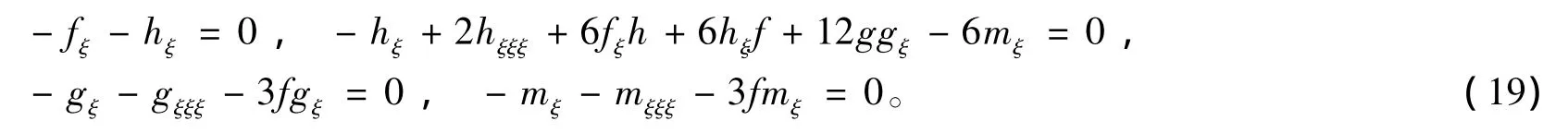
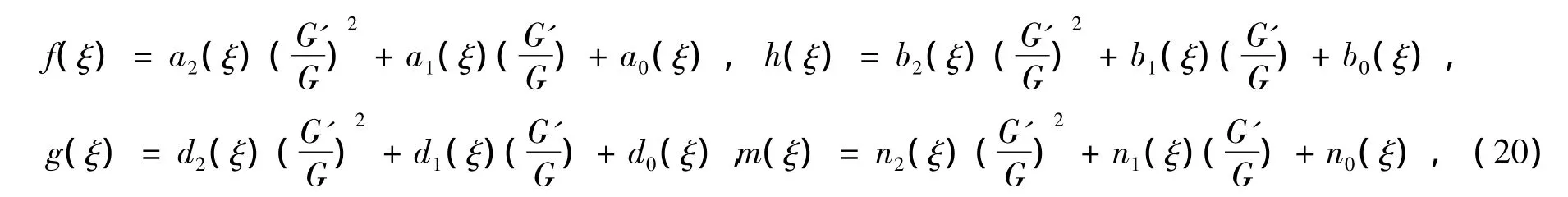
其中，G=G(ξ)满足二阶线性常微分方程

其中，λ、μ 是任意常数;ai、bi、di和 ni(i=0，1，2)是待定函数。

把式(20)和式(21)代入方程组(13)，并按(G')的次数合并同类项，令(G')的各次方的系数为零G

解代数方程组可得:当λ=0，μ=1时，

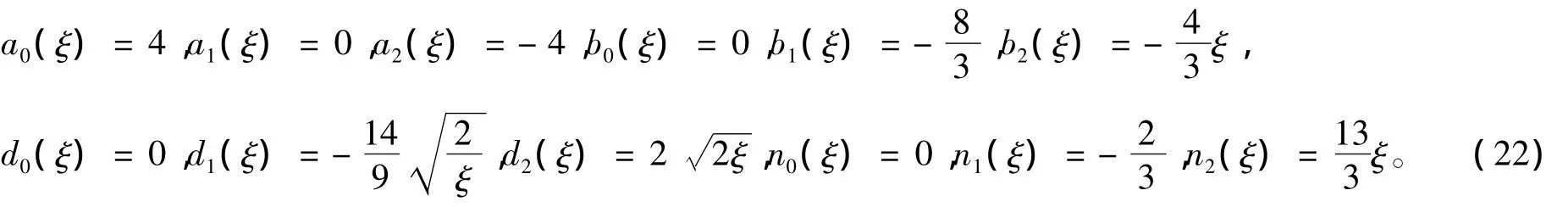
因此，变系数约化方程组(13)的解为

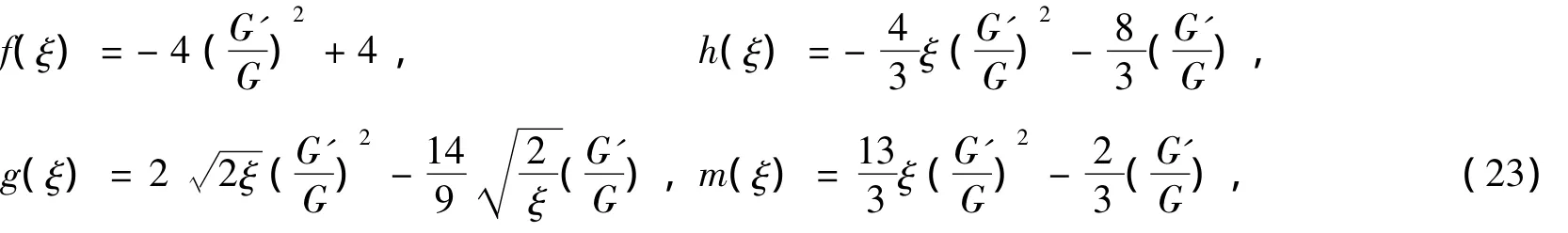
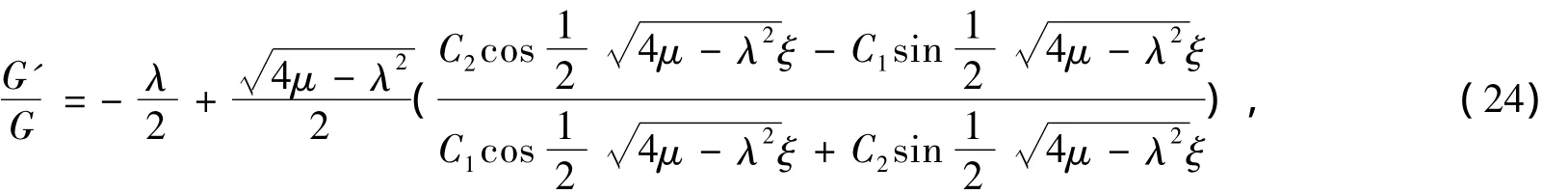
其中，C1、C2是任意常数更多形式的解见文献［10］。

根据式(23)和式(24)就可以得到变系数方程组(13)的解，再联合式(12)可得GIto方程组的解。同时，根据定理1可以得到更广泛的显式解。

为了求解方程(19)，通过齐次平衡，假设方程组(19)具有下述形式的解

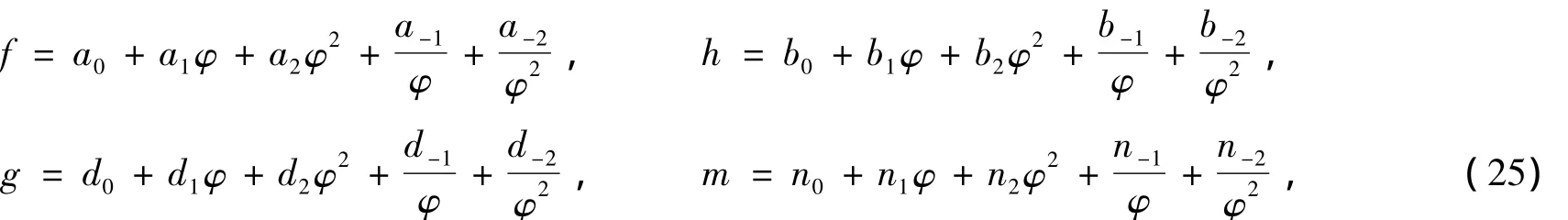
其中，ai、bi、di和 ni(i=0，1，2，-1，-2)是待定常数。

利用辅助方程

其中k是参数。

把式(25)和式(26)代入方程组(19)，令φ(ξ)的系数为零，借助于maple软件和吴消元法［11］，求解关于 ai、bi、di和 ni(i=0，1，2，-1，-2)的超定方程组，可得下述结果

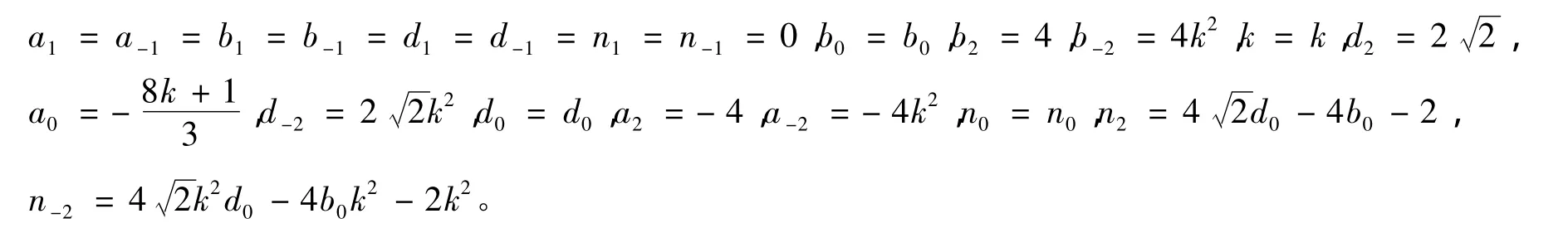
从而可得

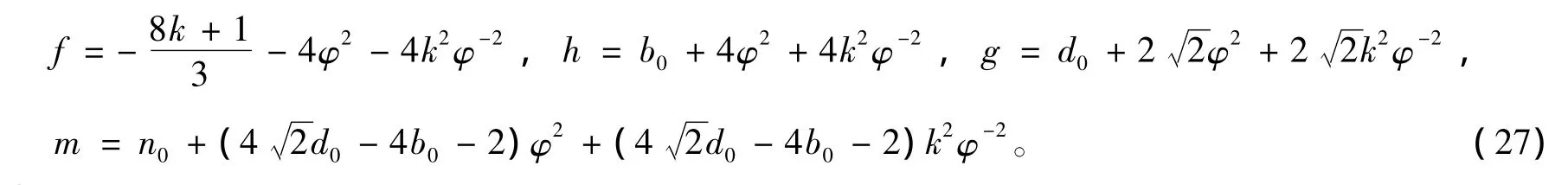
其中，φ(ξ)满足广义Riccati方程并具有下述广义解

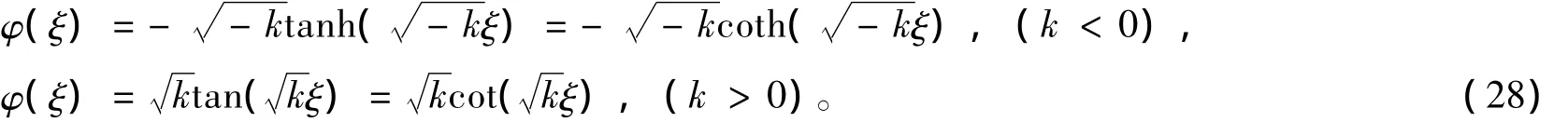
根据式(18)，式(27)和式(28)，可得到原方程组的显式解。同时，将求得的解作为种子解再利用定理1，可以得到方程组(1)的更广泛的显式解。

3 结论

本文利用修正的CK直接方法得到了广义Ito方程组的对称群理论，建立了新、旧解之间的关系，根据定理1，推广了文献［4］中相应的结果。同时，根据对称σ=0与原方程组的相容性，获得了相应的约化方程，通过求解约化方程得到了一些新的显式解。

［1］李画眉，林机，许友生.两组新的广义的Ito方程组的多种行波解［J］.物理学报，2004，53(2):349-355.

［2］Tam H W，Hu X B，Wang D L.Two Integrable Coupled Nonlinear Systems［J］.J Phys Soc Jpn，1999，68(2):369-379.

［3］Ayse K K，Atalay K，Sergei S.Integrability of a Generalized Ito System:The Painlevé Test［J］.J Phys Soc Jpn，2001，70(5):1165-1166.

［4］Zhao Xueqin，Zhi Hongyan，Zhang Hongqing.Improved Jacobi-function Method with Symbolic Computation to Construct New Double-periodic Solutions for the Generalized Ito System［J］.Chaos Solitons Fract，2006，28:112-126.

［5］Fan E.A New Algebraic Method for Finding a Series of Travelling Wave Solution to a Coupled Ito System［J］.J Phys Soc Jpn，2002，71(11):2663-2668.

［6］Robert A，Van G.Solutions to a Novel Casimir Equation for the Ito System［J］.Commun Theor Phys，2011，56:801-804.

［7］Lee J H，Pashaev O K，Rogers C，et al.The Resonant Nonlinear Schrödinger Equation in Cold Plasma Physics Application of Bäcklund-Darboux Transformations and Superposition Principles［J］.J Plasma Phys，2007，73:257-272.

［8］Clarkson P A.Painleve Equations-nonlinear Special Founctions［J］.Appl Math Comput，2003，153:127-140.

［9］Li Biao，Chen Yong，Xuan Hengnong.Generalized Riccati Equation Expansion Method and its Application to the(3+1)-dimensional Jumbo-Miwa Equation［J］.Appl Math Comput，2004，152(2):581-595.

［10］李灵晓，李二强.6阶KdV方程的精确解［J］.河南科技大学学报:自然科学版，2011，32(4):83-86.

［11］Wu W T.Algorithms and Computation［M］.Berlin:Springer，1994.