制冷机冷却风扇转子动平衡技术的研究

张洪彬

(哈尔滨商业大学)

制冷机冷却风扇转子动平衡技术的研究

张洪彬

(哈尔滨商业大学)

基于现场动平衡技术，通过对制冷机冷却风扇转子动平衡性能的分析，推导出制冷机现场动平衡过程中的单位质量影响系数，便可方便地推算出风扇转子的实际配重，从而简便有效的实现现场配重工作。

制冷机;冷却风扇转子;现场动平衡

0 前言

制冷机冷却风扇转子在工作过程中，会经常出现不平衡的状况，是制冷机的常见故障之一，风扇转子的不平衡要引起使用者高度重视，因为它将引起风扇及强烈的振动，但是风扇如果出现不平衡，要是将其解体分析，会很麻烦，因此是否可以在不解体的情况下，实现风扇的现场平衡技术是我们探索的方法之一。基于这种思路，现力求给出一种制冷机冷却风扇转子在不解体的前提下进行现场平衡。

1 建立制冷机冷却用风扇转子振动的数学模型

如图1所示为一制冷机冷却风扇简化的单自由度振动系统图。设转子的转速为n(rpm)，则有ω=2πn/60，那么有相应的关系式

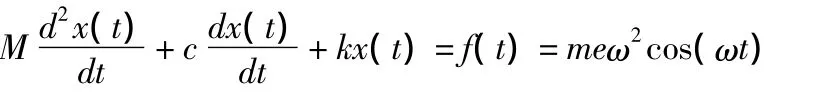
式中:M为风扇的总质量，kg;c为转子的阻尼系数;k为转子的弹性系数;m为转子的偏心质量，kg;e为转子的偏心距，mm;ω为转子的工作频率，Hz;x(t)为风扇振动的幅值响应，mm。

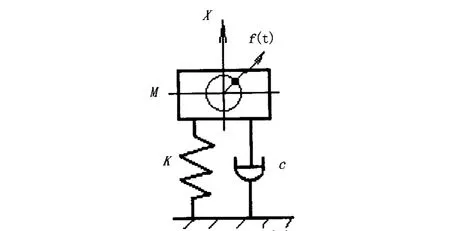
图1 内燃机冷却风扇动力学模型

解此方程，得

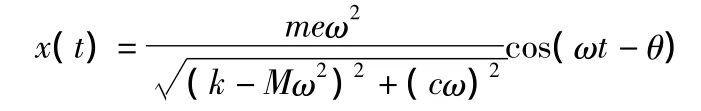
式中:θ为相位差，且

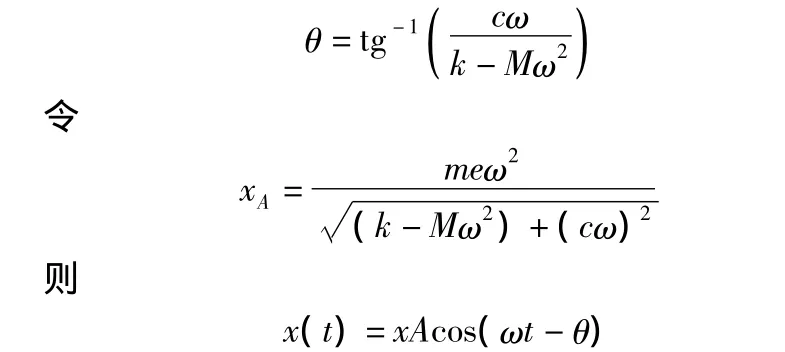
设系统的固有角频率为 ω0，且令 λ =ω/ω0，ζ=ω20/(2M)则

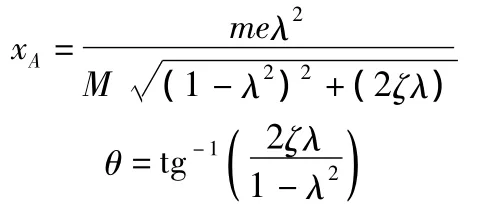
讨论:(1)对于幅频特性:

当 λ ＜ ＜1(λ→0)时，xA→0;

当λ＞＞1时，且ξ很小，xA=me/M=const;

当 λ→1时，xA=me/(2Mξ)，因为 ξ很小，所以 xA出现峰值。

(2)对于相频特性。

当λ→1时，无论ξ多大，θ=π/2;

当 ξ→0，λ 由1-→1时，θ=0;

λ由1+→1时，θ=π/2。

(3)转子不平衡的振动过程。

当转子刚启动时，转子的振动响应为零，随着转速的提高，振幅随之加大，xA↑;

当 n=ω0/(2π)时，xA→me/(2ξ);

当 n＞ ＞ ω0/(2π)时，xA=me/M。

2 不解体情况下制冷机冷却风扇转子现场的动平衡

所谓不解体就是在在不拆卸转子的情况下，在现场安装各种测试传感器，对风扇转子机械系统自身消除me的过程，在现场可直接观测其平衡效果。如图2所示为转子现场动平衡实验装置，其实施现场平衡过程如下。

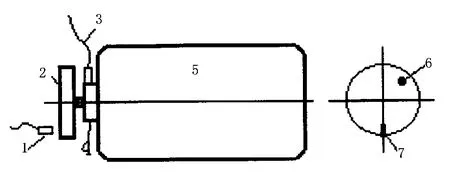
图2 现场动平衡实验装置

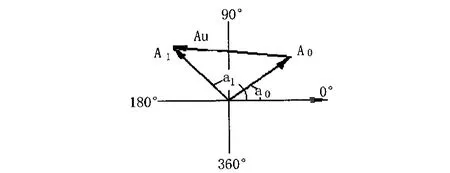
图3 振动量矢量图

第一步:启动制冷机，使欲平衡的转子保持稳定的工作转速n，由振动传感器测得在轴承处的原始振动量为A0，则

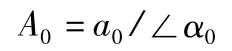
式中:a0为偏心质量;∠α0为偏心质量所对应的相位。

然后降速停机。

第二步:在停机后，在转子上加上一已知试重UT，则

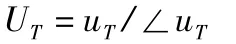
式中:UT为已知试重质量;∠uT为已知配重质量所对应的相位。

第三步:再次开机，使转子再次达到其工作转速n，测得轴承处的振动量为

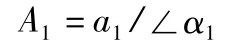
由于振动量呈现线性特性，根据线性系统理论可知，如图3所示A0是由转子原始不平衡量U0引起的，而A1是由U0+UT引起的。故由图3可知

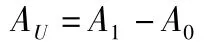
设:单位质量的影响系数为α，则

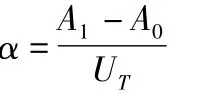
影响系数的物理意义为检测过程中，在转子的圆盘上加装单位质量试重，从而引起转子系统在检测处振动位移的变化量，为矢量计算。

试重消除后，则有

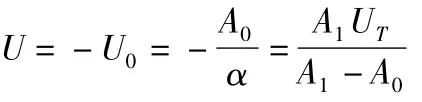
假设不消除其试重，则实际配重为

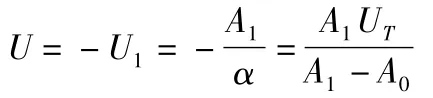
下面用一具体实例进行说明:某工业用制冷机的风扇以1 459.5 rpm逆时针转动，基于不解体检测技术，使用测振仪测得原始不平衡量产生的振幅和相位为:A0=5g/∠-40°。加试重后测得UT=2g/∠-30°，第二次启动后测得数据为A1=9g/∠ -140°。则

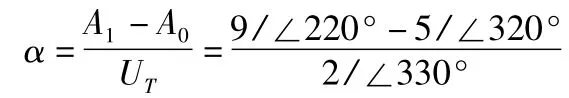
那么将实际试重消除后，有

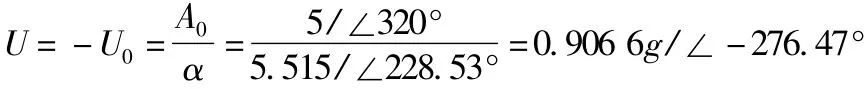
在不消除试重时，有

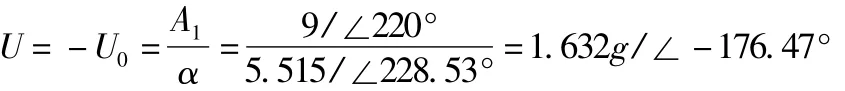
3 结论

本文对制冷机在不解体的情况下，通过对冷却风扇转子不平衡的测试分析，推导出一套制冷机的现场平衡技术，由分析得知制冷机冷却风扇转子为单自由度振动系统，这样，使转子的单位质量的影响系数很容易测得，也就可以方便地计算出风扇转子的实际配重，因此这种方法是在不解体的情况下，在现场较为容易实施的一种平衡方法。

［1］缪道平.活塞式制冷压缩机(第二版)［M］.北京:机械工业出版社，1992.

［2］屈维德.机械振动手册［M］.北京:机械工业出版社，1992.

［3］安胜利.转子现场动平衡技术［M］.北京.国防工业出版社，2007.

［4］倪振华.振动力学［M］.西安:西安交通大学出版社，1988.

U467

C

1008-3383(2012)01-0090-02

2011-10-18

张洪彬(1985-)，男，研究方向:热能与动力工程。