基于STFT的卫星导航接收机抗干扰算法研究

申蕾蕾，张会生，李立欣

（西北工业大学 陕西 西安 710129）

卫星导航系统在军事和民用领域越来越广泛的应用，同时也暴露出自身存在的一些问题[1]。由于卫星导航信号自身的局限性，使得无论是军用还是民用的卫星导航接收机都受到或多或少的影响，在严重的恶意干扰情况下，有可能使整个系统停止工作。因此卫星导航系统的抗干扰研究具有十分重要的意义[2]。

时频分析是同时在时域和频域描述信号的分析方法，将时频联合处理应用到卫星导航接收机抗干扰技术中更是有着较好的前景。同时域滤波技术和频域滤波技术相比，时频域滤波技术的干扰抑制性能有大幅度的提高，因而引起了广泛的关注和研究。其中，STFT（Short Time Fourier Transform）是最简单、最直观的一种时频分布。通过对混有干扰的接收信号进行STFT变换，将信号变换到另一个变换域进行处理。在新的变换域，由于时频变换对干扰信号具有非常好的聚集性，干扰信号呈现出能量的高度聚集，利用窄带滤波或遮隔运算抑制掉干扰信号的能量，从而去除干扰[3]。但是由于STFT固定的时窗宽度使得时频分辨率也是固定的，它内在具有时间分辨力和频率分辨力的矛盾，干扰信号的“局部”平稳性很难保证。本文提出的是一种修正的STFT算法，在STFT算法的基础上，通过对窗函数在时间尺度上的变换，实现时频分辨率随信号频率变化自动可调，克服了STFT分析所有窗口的大小固定不变的缺陷，为非平稳信号的处理提供了强有力的工具。

1 基本STFT算法

STFT算法的基本思想是：傅立叶分析是频域分析的基本工具为了达到时域上的局部化，在信号傅立叶变换前乘上一个时间有限的窗函数，并假定非平稳信号在分析窗的短时间间隔内是平稳的，通过窗在时间轴上的移动从而使信号逐段进入被分析状态，这样就可以得到信号的一组“局部”频谱，从不同时刻“局部”频谱的差异上，便可得到信号的时变特性[4]。

给定一个时间宽度很短的窗函数h（t），让窗滑动，则信号 x（t）的 STFT 定义为：

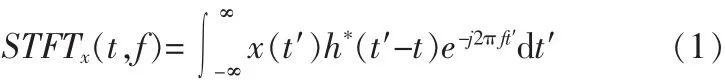
式中*代表复数共轭，x（t）为卫星导航接收信号，一般由有用信号、干扰和噪声组成：

其中，n（t）为均值为零的加性高斯白噪声。

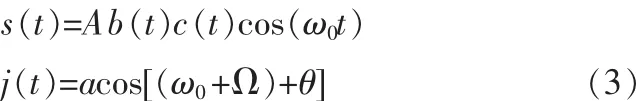
式（3）中 ，A，a为 幅 值 ，b（t）为 接 收 到 的 卫 星 导 航 数据，c（t）为伪随机码，ω0为载波频率，Ω 为频偏，θ为在[02π]上均匀分布的随机相位。

由式（1）可见，正是由于窗函数h（t）的存在，使得短时傅立叶变换具有了局限特性，它既是时间的函数，也是频率的函数。 对于给定的时间t，STFTx（t，f）可看作是该时刻的频谱。信号x（t′）在时间t处的短时傅立叶变换就是信号乘上一个以t为中心的“分析窗”h（t′-t）后所作的傅立叶变换。 因为信号x（t′）乘以一个短窗函数h（t′-t）等价于取出信号在分析时间点t附近的一个切片，所以短时傅立叶变换STFTx（t，f）可以理解为信号x（t′）在时间点t附近的傅立叶变换，即“局部频谱”[5]。

在上面的信号处理中，窗函数起着关键的作用，所加的窗函数能否正确反映信号的时频特性，与窗函数及其长度有关。与当前信号最佳匹配的窗，满足信号x（t）的时-频域上的信号支撑TBP最小。

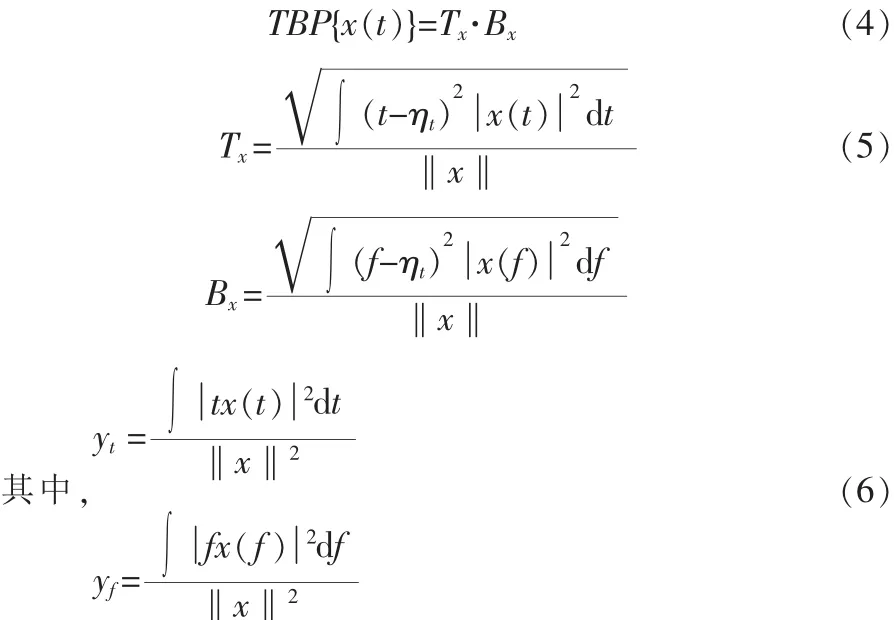
窗函数长度的选择由于Heisenberg测不准原理[6]的影响，使得STFT变换的时间分辨率和频率分辨率之间存在矛盾。STFT算法的缺陷是对于窗函数一旦选则在整个分析过程中都使用相同的窗，其分辨率在时间-频率平面上的所有局域都是相同的。

2 改进的算法

由于STFT算法中时间分辨率和频率分辨率之间的矛盾，使得STFT算法不适合分析较高及较低频率的信号。为此，对窗函数做些修正，使得成为一个可调的时间-频率窗，当观察高频信号时窗函数自动变窄，而研究低频信号时窗函数自动变宽。

窗函数h（t）通过伸压缩和位移得到窗函数族

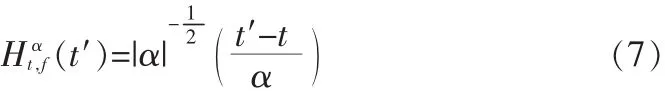
将上式代入到等式（1）中，可得到

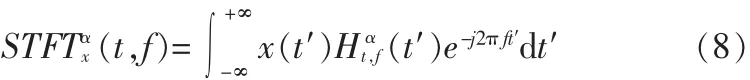
上式为改进的STFT算法的定义。假设窗函数h（t）的中心为τ，半径为 Δh，则函数Hαt，f（t′）是一个中心为t+ατ 且半径为αΔh的一个窗函数。因此，式（8）定义的改进STFT算法给出了信号x（t）在时间窗：

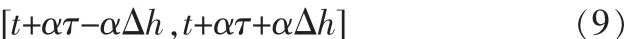
的局部信息，相比于基本STFT算法时间窗

由式（9）定义的时间窗对于小的α值变窄，对于大的α值变宽。

令H（f）为窗函数h（t）的 Fourier变换，设它的中心频率为f*，半径为 Δf，则时间窗Hαt，f（t′）的Fourier变换为中心频率为f+f*/α，半径为 Δf/α 的Hα（f），则改进窗函数的频率范围为

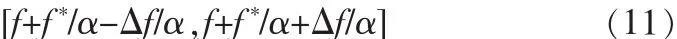
频率带宽为2Δf/α，与变换因子α成反比。

结合式（9）和式（11）可以看出，当α为较小值时，即频率较高时，时间窗变窄；当α为较大值时，即频率较低时，时间窗变宽。改进的STFT算法克服了传统STFT算法的缺陷。

3 计算机仿真

3.1 干扰抑制模型的建立

图1为基于改进算法的干扰抑制模型，其中接收机输入信号就是式（2）定义的x（t），对这个接收信号进行改进STFT，将其映射到时频面上，扫频每个频率点f所在的时间段，对大于检测门限时频点进行遮隔处理，对通过处理后的信号进行ISTFT，将其变换回时域，得到干扰抑制后的信号。

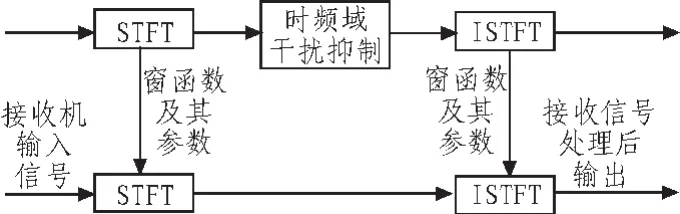
图1 基于改进算法干扰抑制模型Fig.1 The interference suppression model based on improved algorithm

3.2 两种算法对干扰抑制的仿真

图2中，（a）图为无干扰时接收机信号的功率谱密度。（b）图为加入0.1 MHz窄带干扰后信号功率谱密度，对比（b）图和（a）图可以发现在4 MHz频率附近有明显的干扰。（c）图为传统STFT算法抑制干扰后的信号功率谱密度，可以看到，（c）图中4 MHz频率附近的干扰被抑制了一部分，但仍然比较明显。（d）图为改进STFT算法抑制干扰后信号功率谱密度，对比（c）图可以看出，改进STFT算法比传统STFT算法的干扰抑制效果多5 dB，同（a）图比较，接收信号的干扰基本抑制掉了。

由上图可以看出，利用传统STFT算法和改进STFT算法抑制干扰后，信号的误码率明显降低，并且改进算法要优于传统算法。随着SNR的增大，3条曲线更加接近，改进算法抑制干扰后信号的误码率更加接近无干扰时信号的误码率。

4 结 论

文中在深入分析时频域STFT算法的基础上对其缺陷进行改进，提出了一种改进了的STFT算法，并将其应用到卫星导航接收机抗干扰中。利用文中方法，使STFT算法不再受固定时间窗函数时间分辨率和频率分辨率相互制约的约束，从而保证了算法可以处理高频率和低频率的信号。仿真结果表明，文中方法在抗干扰性能和误码率方面要优于传统的STFT算法。总体来说本文所提方法计算量小、抗干扰效果好，是一种简单实用的抗干扰有效方法。

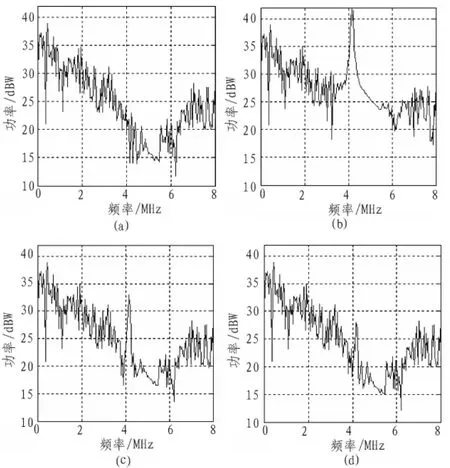
图2 4种情况下功率谱密度对比图Fig.2 The figures of power spectral density in four situations

[1]叶宝盛.GNSS抗干扰接收机技术研究[D].成都：电子科技大学，2010.

[2]王运东，徐锦，李军，等.GPS接收机系统的抗干扰技术[J].舰船电子工程，2006，26（3）：31-39.

WANG Yun-dong，XU Jin，LI Jun，et al.The anti-jamming technology of GPS receiver[J].Ship Electronic Engineering，2006，26（3）：31-39.

[3]徐立.卫星导航接收机时频联合干扰抑制算法研究 [D].成都：电子科技大学，2008.

[4]张细政.一种新的基于时频分析扩频通信去干扰技术[J].湖南工程学院学报，2004，14（4）：50-54.

ZHANG Xi-zheng.A new anti-jamming technology based on time-frequency analysisforspectrum communication[J].Hunan Institute of Engineering，2004，14（4）：50-54.

[5]栾海妍，江桦，刘小宝.自适应短时傅立叶变换算法的研究[J].通信技术，2007，40（8）：217-222.

LUAN Hai-yan，JIANG Hua，LIU Xiao-bao.The study if adaptive short time Fourier transform algorithm[J].Communication Technology，2007，40（8）：217-222.

[6]张贤达.现代信号处理[M].2版.北京：清华大学出版社，2002.