基于GA与L-M优化算法的变压器故障诊断研究

王雅娟，张湧涛

（河北联合大学 电气工程学院，河北 唐山 063000）

近年来，各国专家都致力于变压器故障诊断的人工智能方法的研究。人工神经网络以其独特的容错、联想、推测、记忆、自适应、自学习和处理复杂模式等优点，在电力变压器故障诊断中得到了应用，效果较好[1]。本文利用MATLAB环境构造了一个用于变压器故障诊断的BP网络模型，利用遗传算法对BP神经网络的初始权值和阈值进行优化，然后采用LM（Levenberg-Marquardt）优化算法对BP神经网络进行训练；仿真结果证明，此网络模型精确度较高，可用于变压器的故障诊断。

1 理论基础

1.1 BP神经网络

BP神经网络是一种采用了误差反向传播 （Error Back Propagation，简称BP）算法的单向传播的多层前馈网络，它分为输入层 （Input Layer）、 隐含层 （Hidden Layer） 和输出层（Output Layer）。网络除输入层节点外，有一层或多层的隐含层节点，同层节点之间没有任何连接[2]。输入信号从输入层节点依次传过各隐含层节点，然后传到输出节点，每一层节点的输出只影响下一层节点的输出。BP网络可以看作是一个从输入空间到输出空间的高度非线性映射。在多层前馈网的应用中，单隐含层BP网络的应用最为广泛，其网络结构如图1所示。

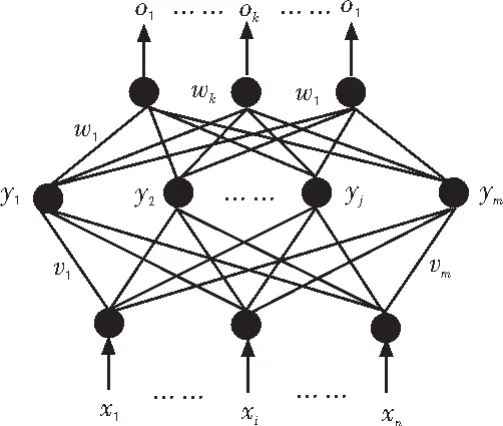
图1 BP神经网络结构Fig.1 BP neural network structure

在 3 层的 BP 神经网络中，输入向量为X=（x1，x2，…，xi，…，xn）T，如果加入xo=-1，可为隐含层神经元引入阈值。隐含层输出向量为Y= （y1，y2...，yj..，ym）T，如果加入y0=-1，可为输出层神经元引入阈值。输出层的实际输出向量为O=（o1，o2，...，ok，...，ol）T，期望输出向量为d=（d1，d2...，dk...，dl）T。 输入层到隐含层之间的权值矩阵用V表示，V=（v1，v2...，vj..，vm）T，其中列向量Vj称为隐含层第j个神经元对应的权向量；隐含层到输出层之间的权值矩阵用W表示，W=（w1，w2...，wk..，wl）T其中列向量wk称为隐含层第k个神经元对应的权向量。各层信号之间的关系可用如下的表达式表示：

对于输出层，有：

对于隐含层，有：

以上4式共同构成了BP神经网络的数学模型。

基于BP算法的神经网络通过多个具有简单处理功能的神经元的复合作用，使网络具有非线性映射能力，由于BP算法的训练是基于误差梯度下降的权重修改原则，其结果不可避免的存在局部极小，收敛速度慢和引起振荡效应等问题[3]，因此用于变压器故障诊断中尚存在一定缺陷。

1.2 遗传算法

遗传算法是根据生物进化思想而得到的一种全局优化算法[4]，在本质上是一种不依赖具体问题的直接搜索方法，仅需给出目标函数的描述，便可从一组随机产生的称为 “种群（population）”的初始解开始搜索，通过个体的“适应值”来评价个体的好坏，被选择的下一代染色体经过交叉和变异等操作产生新的个体。经过上述的反复迭代计算，最终会收敛到最好的个体，即问题的解。由于遗传算法善于全局搜索，且能以较大的概率找到全局最优解，故用它来完成前期搜索能较好的克服BP算法的局部极小的缺陷[5]。遗传算法优化BP网络流程图如图2所示。

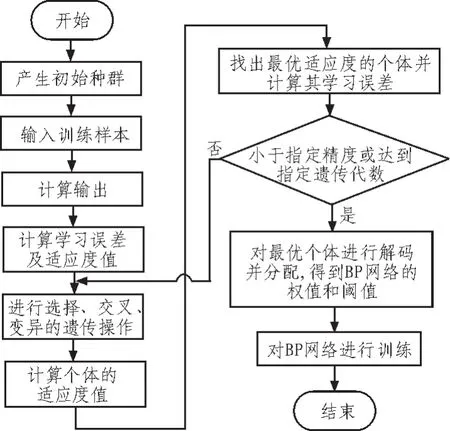
图2 遗传算法优化BP网络流程图Fig.2 Flow chart of BP network optimization by genetic algorithm

遗传算法优化BP神经网络初始值的步骤如下：

1）编码，遗传算法先将解空间的解数据表示成遗传空间的基因型串结构数据，他们的不同组合就构成了不同的点，编码方式有二进制编码和浮点编码，因为浮点编码计算精度较高故本文采用浮点编码。

2）随机产生初始种群。采用随机的方式产生若干个初始串结构数据，每个串结构数据代表一个个体，全体初始串结构数据构成了初始种群。种群的大小一般是20～100，这样既可以提高遗传算法的稳定性，又能够保证种群的多样性，容易获得全局最优解。

3）确定适应度函数。一般以误差函数的倒数作为染色体的评价函数，计算每条染色体的适应度，误差越大，适应度值越小。误差为式（5）所示：

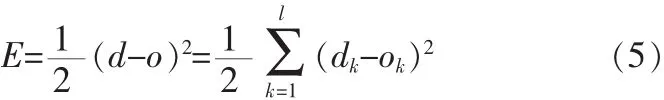
适应度取误差的倒数，即：

4）选择若干适应度函数值大的个体直接进入下一代，适应度值小的个体被淘汰。

5）利用交叉算子（pc）、变异算子（pm）等遗传算子对当前一代群体进行处理，并产生下一代群体。

6）重复步骤 3）4）5），对新一代群体进行新一轮迭代，直到训练目标满足终止条件为止。

1.3 L-M算法

由于标准BP算法的收敛速度慢，会浪费大量时间并且神经网络极易陷入局部极小，因此本文采用Levenberg-Marquardt算法，它是一种树枝优化算法，是高斯-牛顿法的改进，它可以提高BP神经网络的学习速度，加快网络的收敛，避免陷入局部极小[6]。对于3层前馈网络，假定r维向量x是包含所有权值w和偏差b的列向量，即：

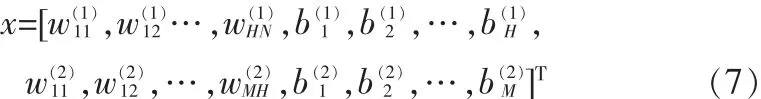
式中：N、H、M分别为网络输入层、中间层和输出层的神经元数。若J为误差对权值微分的Jacobin矩阵，则网络对权值的修正率满足式（8）：

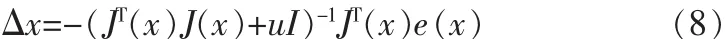
式中：u为自适应调整参数，是个常数；I为单位阵。

2 建模与仿真

2.1 变压器故障诊断的BP建模

神经网络工具箱是以人工神经网络理论为基础，在MATLAB环境下开发出来的众多工具箱中的一种，神经网络工具箱提供了很多经典的学习算法，调用工具箱能够快速实现对实际问题的建模，网络设计，网络优化和结果仿真等工作[7]。文中的BP建模过程如下：变压器油中溶解气体分析数据在一定程度上能反映故障的类型，文中将5种特征气体 （氢气H2，甲烷 CH4、乙烷 C2H6、乙烯 C2H4、乙炔 C2H2）在变压器油中的实际含量作为神经网络的输入向量，即神经网络输入层包括5个神经元；笔者对变压器故障类型进行分析以后，将输出向量确定为5种：无故障，中低温过热（150～700℃），高温过热（一般高于700℃），低能量放电和高能量放电。对于有教师学习的BP网络，故障编码如表1所示，若输出为1，则表示有该类故障，若输出为0，则表示没有该类故障。若为低温过热高能量放电，则输出为01001。

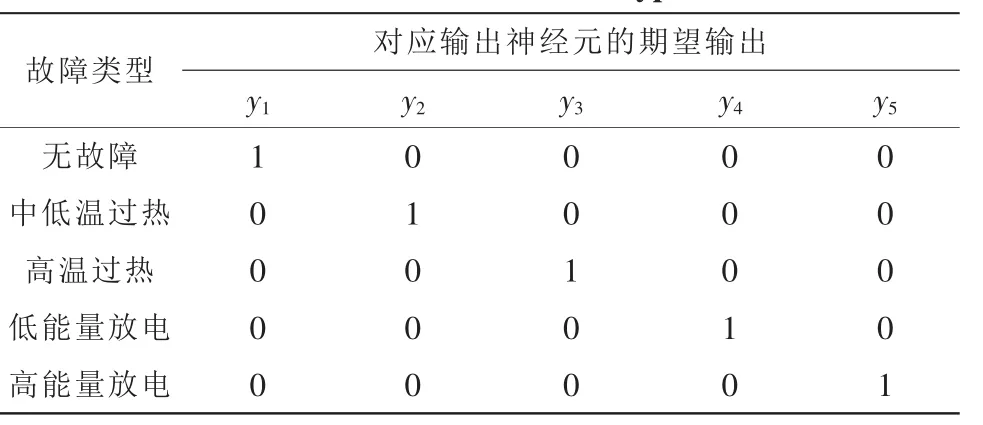
表1 故障类型编码Tab.1 Encode of fault type

2.2 BP网络的训练及仿真

作者收集了已明确故障类型的样本数据72组，随机选取57组作为训练样本集，剩下的15组作为检测样本集。在BP神经网络变压器故障诊断中，一般要对数据进行预处理。如果直接用原始数据作为网络的输入向量，则可能导致因数据误差较大而导致收敛性下降，甚至不收敛。数据预处理是指通过变换处理将网络的输入、输出数据限制在（0，1）或（-1，1）区间内。本文MATLAB仿真中就是利用mapminmax（）函数对所有数据样本做了归一化处理，使其变换到（0，1）区间内，其MATLAB编码如下：

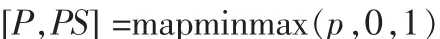
其中，p为原始输入向量，P为数据归一化后的输入向量，规范化的映射记录在结构体PS中。

文中的BP网络输入层取5个节点，输出层取5个节点，对于如何确定BP网络隐含层中神经元的个数，往往需要根据设计者的经验和多次试验来确定，因而不存在一个理想的解析式来表示。本研究中，笔者经过多次尝试，最后确定隐含层神经元个数为11，即构成了一个5-11-5的BP神经网络。将GA和BP结合起来，形成BP-GA混合算法，以GA优化BP网络的初始权值和阈值，再由BP算法按负梯度方向修正网络权值和阈值，进行网络训练[8-9]。用遗传算法对BP网络的初始权值阈值进行优化的过程：过程中采用浮点型编码，遗传算法的种群中的个体数目为50，遗传代数为100。采用遗传算法工具箱函数编程如下：

[x，endPop，bPop，trace]=ga（aa，‘gabpEval’，[]，initPpp，[1e-6 1 0]，‘maxGenTerm’，gen，...

表2 不同训练函数训练效果比较Tab.2 The training effect comparison of different training function

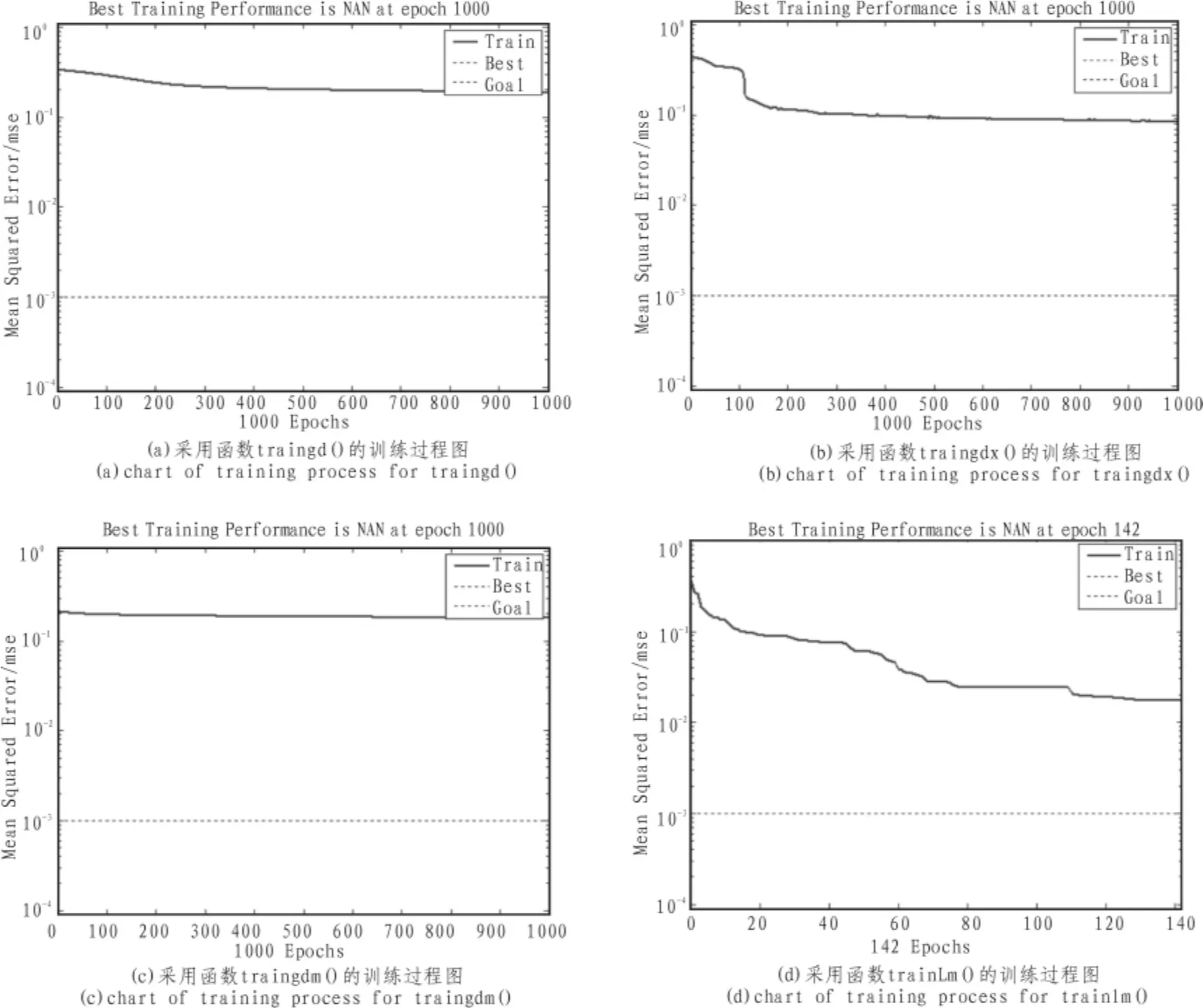
图3 采用不同训练函数的训练过程图Fig.3 Chart of neural network training process for different training functions

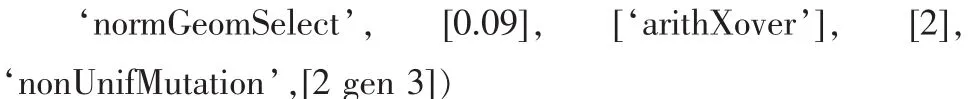
遗传编码的长度为S=R×S1+S1×S2+S1+S2，其中R为输入向量个数，即R=5；S2为输出向量个数，即 S2=5；S1为隐含层节点数，即S1=11。将S按此式做分配后分别成为BP网络的输入层和隐含层的初始权值与阈值。变压器故障诊断的BP网络的生成调用的主要函数如下：

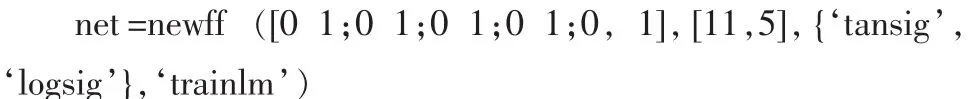
[0 1；0 1；0 1；0 1；0 1] 分别定义了输入层各神经元的最小输出值（为0）和最大输出值（为1）。由于输出模式为0-1，因此本网络隐含层神经元的传递函数采用S型正切函数tansig（），输出层神经元的传递函数采用S型对数函数logsig（），这样正好满足了网络的输出要求[9]。由于标准BP算法的收敛速度慢，会浪费大量时间并且神经网络极易陷入局部极小，梯度下降算法（（））、动量及自适应梯度递减算法（（））、梯度下降动量算法（（））和算法（（））分别对同一训练样本进行训练。训练结束后记录训练时间（）和训练误差（），比较结果如表2所示。不同训练函数的网络训练的过程图如图3所示。

网络训练参数设置如下：

设置好网络训练参数以后，开始调用神经网络工具箱中的train（）函数对网络进行训练，调用格式如下：

其中P为输入向量，T为输出向量。

将检验样本数据进行归一化处理后开始做仿真处理，MATLAB代码如下：

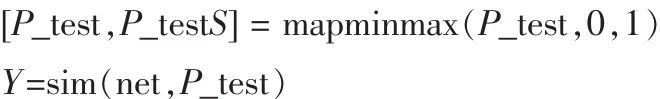
式中：P_test[]为待检验数据样本集。最后，此遗传神经网络的训练图如图4所示。

图4 神经网络训练图Fig.4 Chart of neural network training process

检验样本的诊断结果如表3所示。

表3 检验样本的诊断结果Tab.3 Diagnostic test results of samples

从上表可以看出，对于BP神经网络第7和12组数据同期望输出之间出现了偏差，故障诊断率为73.3%；对于遗传神经网络只有第7组数据统期望输出之间出现了偏差，故障诊断率为93.3%。利用遗传算法优化避免了BP网络易陷入局部极小的问题，达到了优化网络的目的，优化后的BP网络诊断模型故障诊断准确率得到了很大的提高。

3 结 论

提出了一种基于遗传神经网络的变压器[10]故障诊断的方法。它采用3层BP神经网络作为诊断模型，利用遗传算法优化该神经网络的初始权值和阈值，并采用L-M优化方法对该神经网络进行训练，最终加快了收敛速度，并提高了诊断识别的精度。从以上数据结果分析，该网络模型能够比较精确地达到目标结果，使变压器故障诊断准确率提高到了93.3%，从而证实了此方法的正确性和有效性，证明利用遗传神经网络与L-M算法的结合可以较好地解决变压器故障诊断问题。

[1]飞思科技产品研发中心.Matlab6.5辅助神经网络分析与设计[M].北京：电子工业出版社，2003.

[2]杨海马，刘瑾，张菁.BP神经网络在变压器故障诊断中的应用[J].变压器，2009，46（1）：67-70.

YANG Hai-ma，LIU Jin，ZHANG Jing.BP neural network for transformer fault diagnosis[J].Transformer，2009，46（1）：67-70.

[3]魏本征，田质广.基于遗传优化BP网络的汽轮发电机故障诊断[J].控制工程，2007，14：175-177.

WEI Ben-zheng，TIAN Zhi-guang.Diagnosis of steam turbine generatorbased on genetic BP network [J].Control Engineering，2007，14：175-177.

[4]符杨，蓝之达.遗传算法与人工神经网络结合在变压器故障诊断中的应用[J].变压器，2003，40（10）：32-37.

YU Yang，LAN Zhi-da.Transformer fault diagnosis based on genetic algorithm and artificial neural network[J].Transformer，2003，40（10）：32-37.

[5]杨凡，米根锁.BP网络结合遗传算法在故障诊断中的应用[J].控制理论与应用，2006，25（11）：4-6.

YANG Fan，MI Gen-suo.BP network and genetic algorithm in fault diagnosis[J].Control Theory and Applications， 2006，25（11）：4-6.

[6]韦灼彬，吴森，高屹.应用遗传算法和L-M优化的BP神经网络模型预测机场道面使用性能[J].空军工程大学学报：自然科版，2009，10（4）：11-16.

WEI Zhuo-bian，WU Sen，GAO Yi.BP neural network prediction model for airport pavement performance based on L-M optimization and genetic algorithm[J].Air Force Engine-ering University：Natural Science Edition，2009，10（4）：11-16.

[7]陈龙，于盛林.遗传神经网络在模拟电路故障诊断中的应用[J].计算机仿真，2007，24（9）：293-296.

CHEN Long，YU Sheng-lin.Genetic neural network in analog circuit fault diagnosis[J].Computer Simulation，2007，24（9）：293-296.

[8]储诚山，张宏伟，郭军.基于遗传算法和BP神经网络的用水量预测[J].中国农村水利水电，2006（4）：36-39.

CHU Cheng-shan，ZHANG Hong-wei，GUO Jun.Water demand based on ggenetic algorithm and BP neural network[J].China Rural Water and Hydropower，2006（4）：36-39.

[9]梁科，夏定纯.MATLAB环境下的遗传算法程序设计及优化问题求解[J].开发研究与设计技术，2010（1）：1048-1050.

LIANG Ke，XIA Ding-chun.Genetic algorithm optimization program design and problem ssolving in matlab environment[J].Development and Design Techniques，2010（1）：1048-1050.

[10]赵永雷，黄家栋，李配配.基于加权模糊C均值聚类算法的变压器故障诊断[J].陕西电力，2011（9）：39-41.

ZHAO Yong-lei，HUANG Jia-dong，LI Pei-pei.Fault diagnosis on transformer based on weighted fuzzy C-means clustering algorithm[J].Shaanxi Electric Power,2011（9）：39-41.