MATLAB在强心苷比较中的应用

徐文丽，姜忠华

（1.电子科技大学 数学科学学院，四川 成都 611731；2.电子科技大学 物理电子学院，四川 成都 610054）

MATLAB在强心苷比较中的应用

徐文丽1，姜忠华2

（1.电子科技大学 数学科学学院，四川 成都 611731；2.电子科技大学 物理电子学院，四川 成都 610054）

首先根据药物动力学的房室分析理论，建立口服药物动力学模型，推导出多次给药的血药浓度计算公式，并对模型作了参数识别；其次根据相关资料设计出用药方案，根据所建立的药物动力学模型，使用相关数据，分别计算出多次用药后的血药浓度值及其变化，而且还绘制出了两种给药方案的药时曲线，其中计算和绘图都利用了MATLAB计算软件；最后通过对现有两种方案下的平均稳态血药浓度的分析，针对病人的情况采取最优方案。

MATLAB；算法；心力衰竭；饱和量；维持量

MATLAB语言是当前国际上自动控制领域的首选计算机语言也是很多理工科专业最适合的计算机语言。作为一种程序设计语言，MATLAB提供了循环语句结构，条件语句结构，开关语句结构以及与众不同的试探语句。本文中用到了循环语句结构，二维图形绘制语句。图形绘制是MATLAB语言的一大特色。MATLAB中提供了一系列直观、简单的二维图形绘制命令与函数，可以将实验结果和仿真结果用可视的形式显示出来。假设用户已经获得了一些实验数据。例如，已知各个时刻t=t1，t2，…，tn，在这些时刻处的函数值y=y（t1），y（t2），…，y（tn），则可以将这些数据输入到 MATLAB 环境中，构成向量t=[t1，t2，…，tn]和y=[y（t1），y（t2），…，y（tn）]，如果用户想用图形的方式表示二者之间的关系，则给出plot（t，y）即可绘制二维图形。这样绘制出的“曲线”实际上是给出各个数值点间的折线，如果这些点足够密，则看起来就是曲线了。可以看出，该函数的调用是相当直观的[1]。

1 建立模型

建立药物动力学模型：设ka为一级吸收速率，k为一级消除速率，t0为口服用药后体内药物吸收达到高峰的时间，x（t）是t时刻体内的药量，c（t）是t时刻血药浓度，xa（t）是吸收部位的药量，V是表观体积，D是用药量，F是生物利用度，且知x（t）=Vc（t）。口服用药体内药量服从一室药物动力学模型如下：

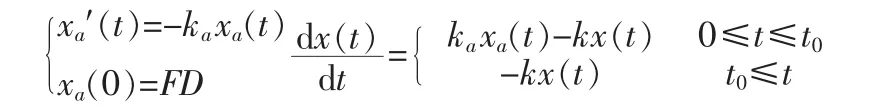
由式可解得第一次单剂口服药量D后，体内的血药浓度为：

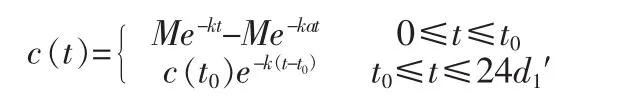
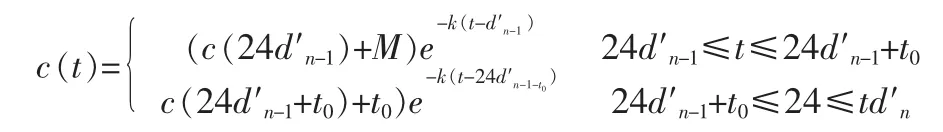
其中d′n-1为第n次口服用药与第一次口服用药间隔的天数[2-3]。

2 数值实验

地高辛为由毛花洋地黄提纯制得的中效强心甙，其特点是排泄较快而蓄积性较小，临床使用比洋地黄片和洋地黄毒甙安全。口服主要经小肠上部吸收，吸收不完全，也不规则，口服吸收率约75%，生物利用度片剂为60%～80%，口服起效时间0.5～2小时，血浆浓度达峰时间2～3小时，获最大效应时间为2～6小时。作用维持4～7天。注射给药易致不良反应，故仅适用于严重心衰需要立即治疗的病人。分布：吸收后广泛分布到各组织，部分经胆道进入肠道而形成肝–肠循环。血浆蛋白结合率低，为20%～25%，表观分布容积为6～10 L/kg。代谢与排泄：地高辛在体内转化代谢很少，主要以原形由肾排除，尿中排出量为用量的50%～70%；地高辛消除半衰期平均为35小时[4]。设此次治疗的疗程为15天，也不考虑其他合并症对治疗的影响。

方案一饱和量疗法方案：前4天，每6小时口服一次地高辛0.25 mg，往后每隔一天服药一次，药量为0.312 5 mg，持续 11 天[5]。

方案二维持量疗法方案：每隔一天服药一次，药量为0.312 5 mg，共 15 天[6-8]。

根据资料和上述公式，可以计算出ka=0.7 hr-1，k=0.016 9 hr-1，F=0.7，V=480 L。 若口服用药是 312.5 μg，则：

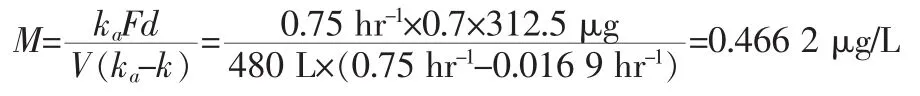
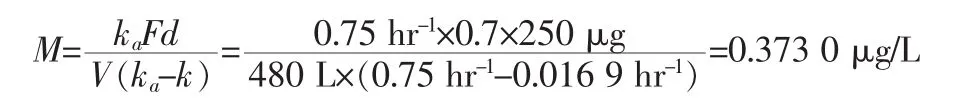
其中，维持量疗法的算法设计如下：

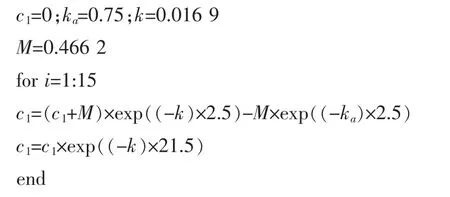
饱和量疗法的算法设计如下：

在饱和量阶段

在维持量阶段

利用MATLAB软件计算出4种用药方法的血药浓度，如表1所示。

若口服用药是 250 μg，则：

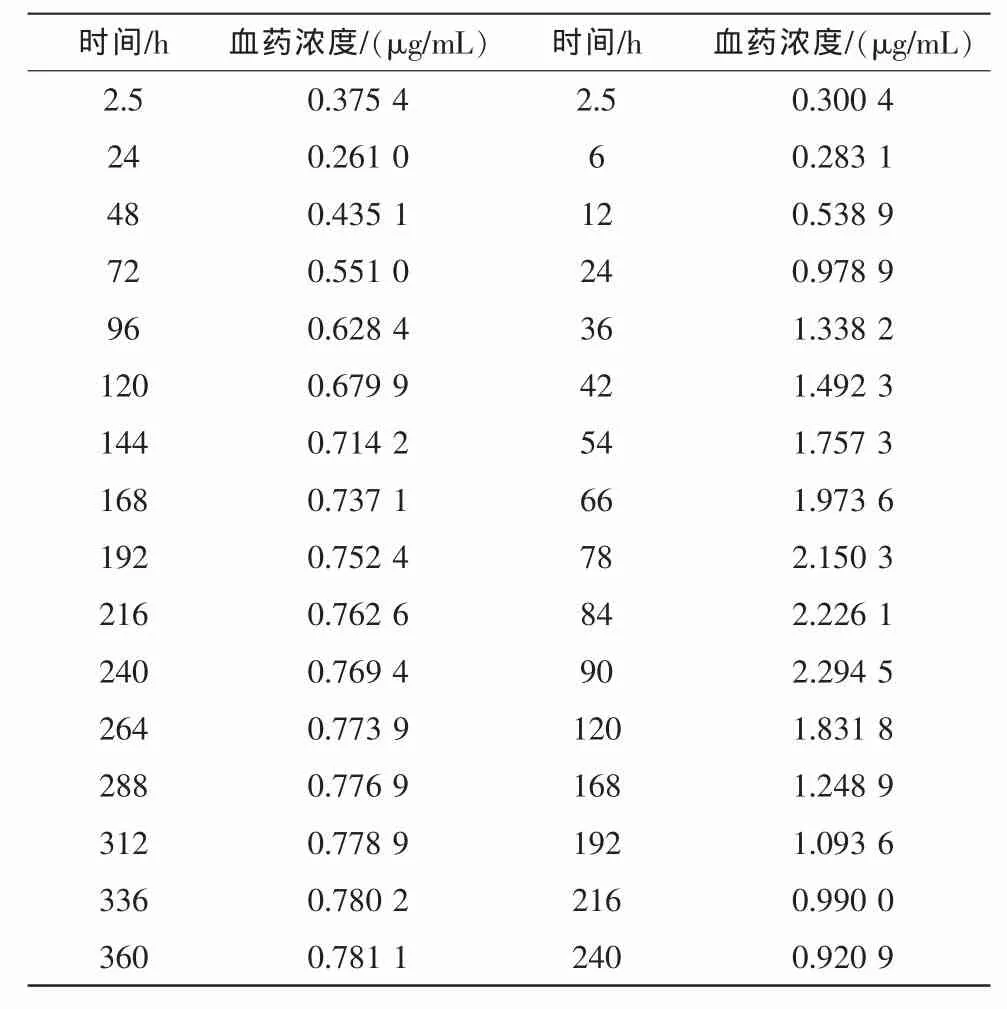
表1 血药浓度Tab.1 Blood drug concentration

根据表中的数据，利用MATLAB软件可绘制出血药浓度的药时曲线如图1～图3所示。

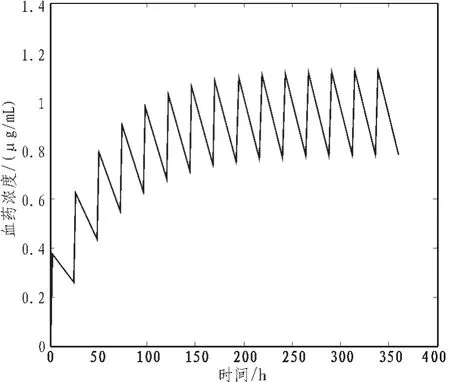
图1 方案一的血药浓度的药时曲线Fig.1 Blood drug concentration curve of plan one

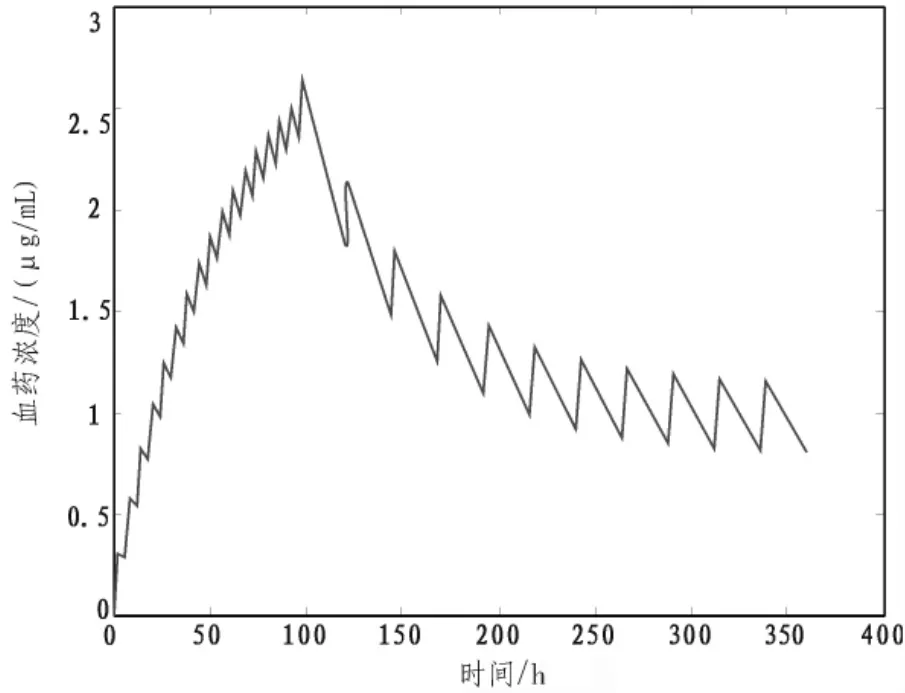
图2 方案二的血药浓度的药时曲线Fig.2 Blood drug concentration curve of plan two

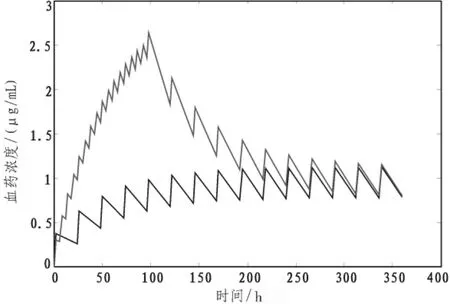
图3 两个方案的比较Fig.3 The comparison of the two scheme

3 结束语

针对心力衰竭的治疗，用饱和量疗法和维持量疗法，分别得到了在两种情况下的血药浓度，利用数值计算结果，分析比较了方案的疗效，在图中可以看出饱和量疗法较维持量疗法稍早达到治疗浓度，但血药浓度有几天处在治疗浓度以上，易中毒，维持量疗法的稳定浓度处于治疗浓度中，所以饱和量疗法适用于急性心衰，维持量疗法适用于慢性心衰。

[1]姜启源.数学建模[M].北京：高等教育出版社，2003.

[2]杨振邦.现代强心苷的临床应用[M].合肥：安徽科学技术出版社，2002.

[3]陈刚.临床药代动力学研究中几个值得注意的问题[J].中国临床药理学杂志，1987（4）：229-234.

CHEN Gang.Clinical pharmacokinetic studies in several noteworthy issues [J]. Chinese Journal of Clinical Pharmacology，1987（4）:229-234.

[4]李冬梅，王树忠，汪琪.阿奇霉素治疗支原体肺炎的序贯疗法定量分析[J].生物数学学报，2007，22 （4）：735-739

LI Dong-mei，WANG Shu-zhong，WANG Qi.Azithromycin know the quantitative analysis of sequential therapy of mycoplasma pneumonia[J].Journal of Mathematical Biology，2007，22 （4）：735-739.

[5]Saif S，Jeptha P，WANG Yong-fei，et al.Association of serum digoxin concentration and outcomes in patients with heart failure[J].JAMA，2003，289（7）：871-877.

[6]陈东彦，李冬梅，汪琪.阿奇霉素资料肺炎支原体用药优化设计[J].工程数学学报，2003，20（8）：35-38.

CHEN Dong-yan，LIDong-mei，WANG Qi.Azithromycin mycoplasma drug information optimization design[J].Chinese Journal of Engineering Mathematics， 2003，20（8）：35-38.

[7]舒玲玉，祝光礼.心衰现代实验研究方法及中医药研究现状[J].浙江中西医结合杂志，2008，18（11）：88-93.

SHU Ling-yu，ZHU Guang-li.Failure of modern experimental methods and research status of traditional Chinese medicine[J].Zhejiang Journal of Integrated Traditional and Western Medicine，2008，18（11）：88-93.

[8]地高辛片说明书[S].上海：上海医药集团有限公司信谊制药总厂，2006.

Application of MATLAB in comparison of cardiac glycosides

XU Wen-li1，JIANG Zhong-hua2
（1.School of Mathematical Sciences，UESTC，Chengdu611731，China；2.School of Physical Electronics，UESTC，Chengdu610054，China）

First of all， according to the atrioventricular pharmacokinetic analysis， the establishment of oral pharmacokinetic model， serum concentrations to achieve the changes， repeated administration of derived plasma concentration formula， and model parameter identification was made， followed by， in accordance with the relevant information to design drug programs，in accordance with established pharmacokinetic model，using the relevant data were calculated after repeated drug plasma concentration and changes in value， but also to map out the two drug programs the drug concentration-time curve， in which computing and graphics are calculated using the MATLAB software， Finally， the two programs under the existing steady-state average plasma concentration analysis of the patient’s condition for the best program to take.

MATLAB；algorithm；heart failure；saturation；maintenance dose

TP301.6

A

1674－6236（2012）06-0031-03

2011-09-27稿件编号：201109162

徐文丽（1984—），女，山东青岛人，硕士研究生。研究方向：大规模线性方程组。