基于t检验的逐步回归的改进

刘 明，王仁曾

（1.兰州商学院 统计学院，兰州 730020；2.华南理工大学 经济贸易学院，广州 510006）

1 问题的提出

逐步回归是线性回归分析中重要的一种分析方法，主要用来解决多元线性回归模型中解释变量个数较多时如何选择解释变量，以使得在回归方程中包含所有对被解释变量影响显著的解释变量而不包含影响不显著的解释变量的问题。逐步回归正是为解决这类问题而设计的一种回归方法。它的主要思路是在所考虑的全部解释变量中按对被解释变量的贡献大小逐个引入回归方程，己被引入回归方程的变量在引入新变量后也可能失去重要性，而需要从回归方程中剔除出去。引入一个变量或者从回归方程中剔除一个变量都要进行F检验，以保证在引入新变量前回归方程中只含有对被解释变量影响显著的变量，而不显著的变量已被剔除[1]。

在逐步回归中每剔除和引入一个变量都需要计算F统计量的值，这需要一定的工作量。同时，逐步回归中所用的F检验对于众多初学者和应用者来说也难以理解和把握，而单个参数显著性t检验是人们所熟知的。笔者通过研究发现，F统计量和t统计量存在紧密的联系，逐步回归中的F检验和参数显著性t检验是等价的，因此可以转而考虑使用t检验。相比较而言，t统计量的计算要比F统计量的计算简便得多，F统计量需要计算复杂的偏回归平方和及剩余平方和，而t统计量只需要计算回归系数的估计值及其估计量的标准差的古计量即可。现代常用的统计软件一般都会计算显示回归模型参数的t检验值，而很少会给出用于逐步回归的F检验值，即便使用计算机，F统计量也不易计算。本文考虑用t检验准则替代F检验准则对多元线性模型进行逐步回归，以简化逐步回归的计算过程。要实现这一目标，需分析逐步回归中的F检验，并完成其与t检验的等价性的证明。

2 逐步回归中的F检验及其与t检验的等价关系

考虑含有k个解释变量的线性总体回归模型式（1）和普通最小二乘法（本文均在普通最小二乘法下讨论样本回归模型）下的样本回归模型式（2）：

首先定义总离差平方和TSS（Total Sum of Squares）、可解释的平方和ESS（Explained Sum of Squares）和剩余平方和RSS（Residual Sum of Squares）：

其中y^i=yi-μ^i为样本拟合值，ȳ为样本均值，n为样本容量。

再定义偏回归平方和。不含xk的样本回归模型（为方便分析，在每一步对解释变量的考察中，本文均以xk为研究代表）

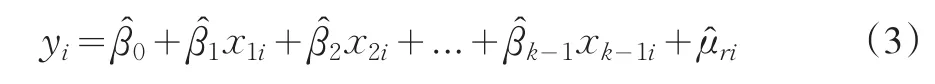
设式（3）的可解释的平方和为ESS*，剩余平方和为RSS*，则xk的偏回归平方和定义为：

按此法即可定义其他解释变量的偏回归平方和。不难看出，ESSPk=RSS*-RSS。

逐步回归中引入（剔除）解释变量的标准是偏回归平方和最大（最小）。在某一引入步骤中，设模型中已含有k-1个解释变量（全部显著），需引入第k个解释变量，原模型和引入变量之后的样本模型即可分别表示为式（3）和式（2）。

这样由第k个解释变量xk的偏回归平方和ESSPk构造的F统计量为：

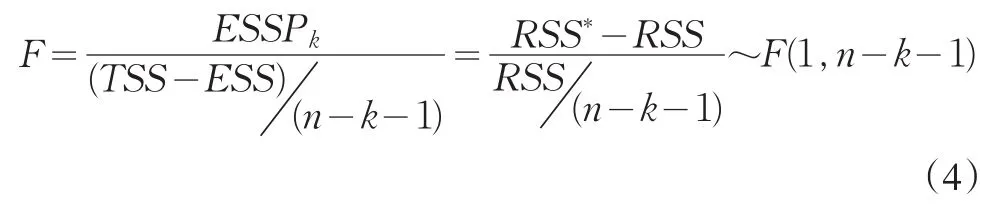
ESS和RSS分别是包含k个解释变量xk的回归模型的可解释的平方和和剩余平方和，RSS*即为未引入新变量的原回归模型的剩余平方和。接下来进行F检验，以判断解释变量xk是否该引入到回归模型中，检验过程不再详述。

在某一剔除步骤中，设模型中已含有k个解释变量（可能存在不显著的解释变量），找到偏回归平方和最小的亦即最可能被剔除这个解释变量，不妨设为xk，原模型和剔除变量之后的样本模型即可表示为式（2）和式（3）。不难发现，由xk的偏回归平方和ESSPk构造的F统计量与引入解释变量过程中的F统计量（4）相同。和引入变量过程一样，接下来进行F检验，以判断解释变量xk是否该从回归模型中剔除。

显然，若能证明逐步回归中的F检验与t检验是等价的，就可以将t检验引入到逐步回归过程中。现在讨论t检验。

以解释变量xk的显著性检验为例，由其系数βk构造的t统计量为：

命题1普通最小二乘法下，用于检验某变量显著性所构造的t统计量的平方等于逐步回归中用于判断是否应剔除（或引入）该变量的F检验所构造的F统计量，即t2=F。

证明：仍以解释变量xk为考察对象。利用OLS法得到xk的系数βk的估计量为[2]：

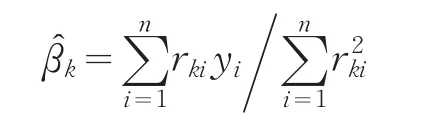
其方差估计量是：

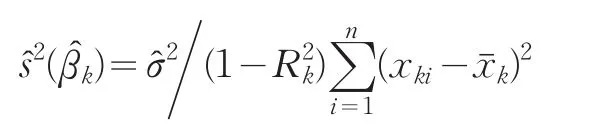
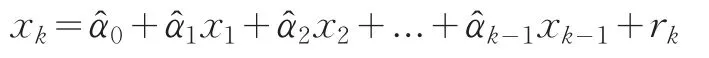
rk是根据OLS法构造的辅助回归模型的残差项。R2k是辅助回归模型的样本可决系数：

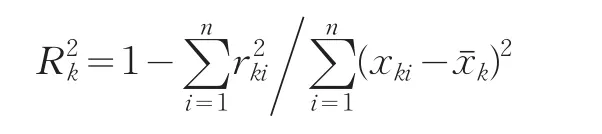
考虑在模型中将xk剔除（或在只包含前（k-1）个解释变量情形下引入），此时构造的F统计量为：

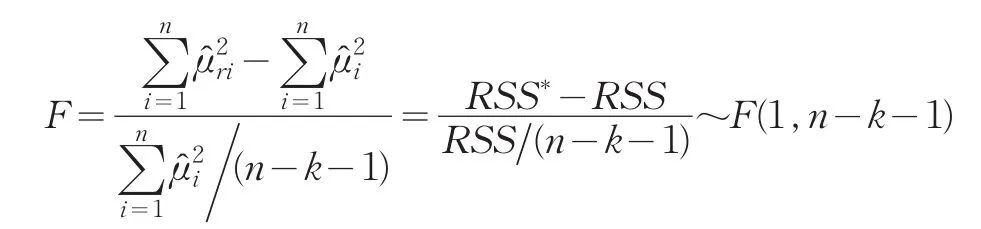
再考虑关于xk的显著性t检验。在βk=0的假设下有：

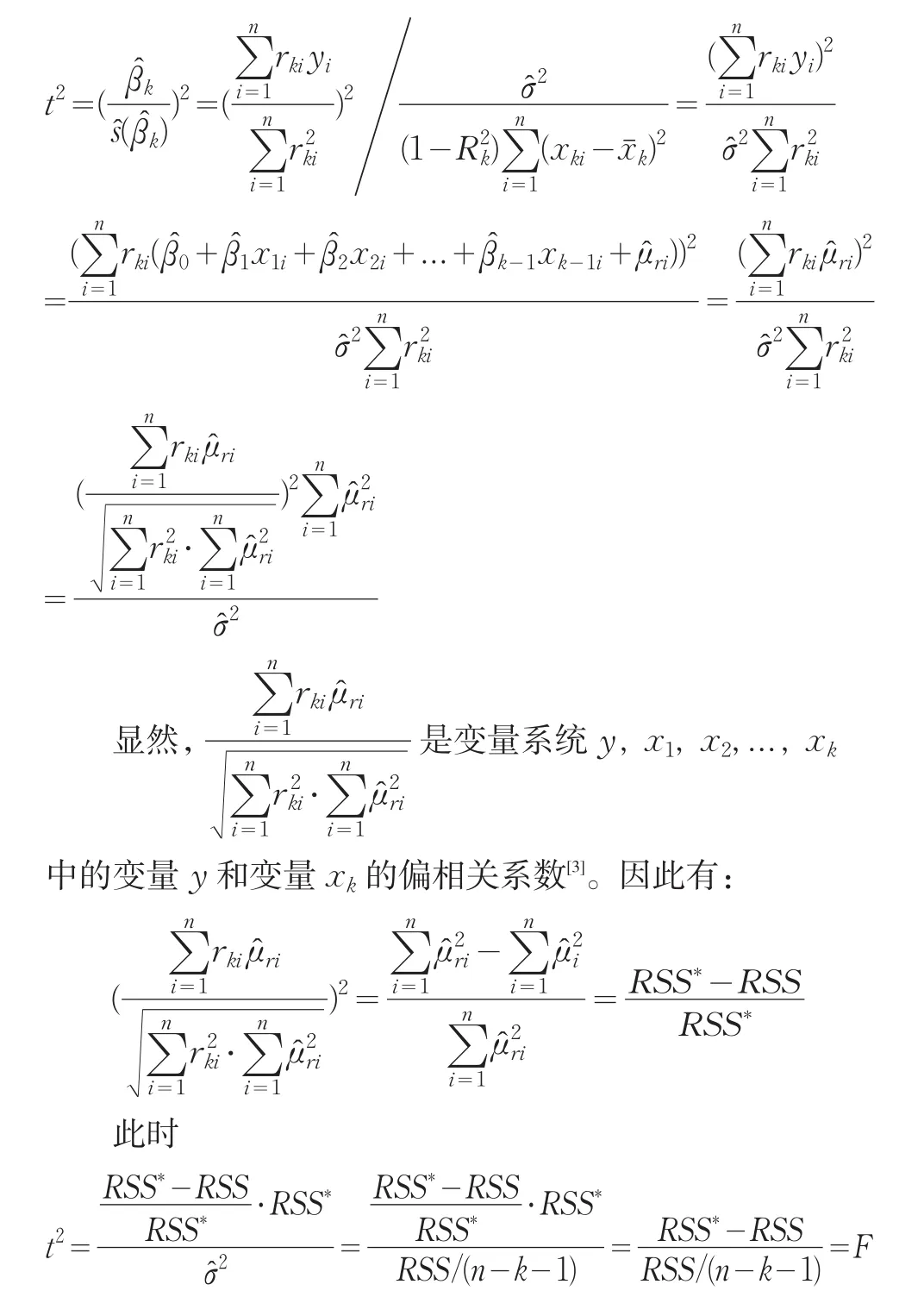
证毕。

由命题1即可得出下述命题2。

命题2 t统计量的平方服从第一自由度为1、第二自由度为n-k-1的F分布，即t2～F(1,n-k-1)。

在检验某一参数的显著性时，t检验进行的是双尾检验而F检验进行的是右单尾检验，虽然两类检验的拒绝域不同，但检验结论一致，这由命题3表述。

命题3当t检验的临界值取tα时，由命题1，F检验的临界值当取，此时两类检验拒绝原假设的概率是相同的，即，其中t～t(n),F～F(1,n)。

证明：自由度为n的t分布的密度函数为[4]：

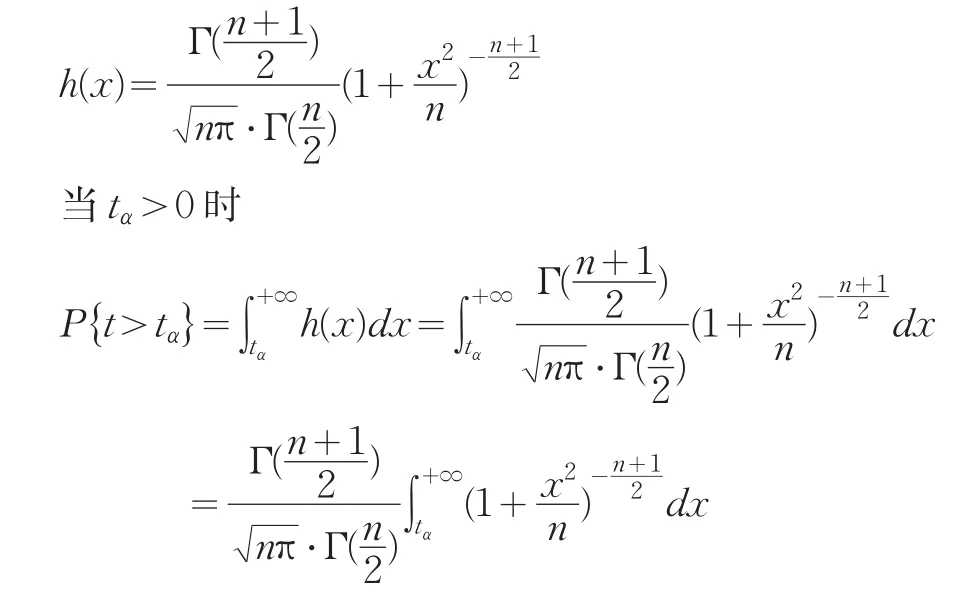
第一自由度为1，第二自由度为n的F分布的密度函数为：因此可得

证毕。

综合命题1、2、3，不难得出结论：在普通最小二乘估计下，线性回归模型的逐步回归中的F检验与显著性t检验是等价的。该结论是用t检验替代F检验来完成逐步回归的依据。

3 基于t检验的逐步回归应用实例

依据以上所证明的结论——逐步回归中所用到的F检验和参数显著性t检验是等价的，可以考虑在逐步回归中使用更便于计算的t检验。使用方法非常简单，只需将逐步回归中作为引入、剔除变量准则的F检验替换为t检验即可。逐步回归的参数求解方法在数学上称为“求解求逆紧凑变化法”，其本质仍是普通最小二乘法，只是在计算过程中考虑了引入、剔除变量的过程，将参数估计的每一步都通过矩阵运算实现了。如果将原来的F检验替换成t检验，对“求解求逆紧凑变化法”计算原理和方法均无影响，模型参数估计可顺利实现。在原逐步回归中，引入或剔除变量的依据是变量的偏回归平方和的大小，在同一引入或剔除的步骤中，偏回归平方和的大小和F统计量的大小是一致的，即偏回归平方和越大，F值越大，偏回归平方和越小，F值越小。由于F统计量和t统计量存在对应关系F=t2，因此t统计量的绝对值 ||t与偏回归平方和也具有同向变动关系： ||t越大，偏回归平方和越大， ||t越小偏回归平方和越小。因此可以把 ||t作为引入和剔除变量的标准。原逐步回归过程中构造的第一个回归模型是只引入一个解释变量的一元回归模型，当改用t统计量作为变量引入、剔除的准则后，为简化计算步骤，首先构造的是一个包含所有解释变量的线性回归模型，在该模型中寻找被剔除的变量，其标准是未通过显著性t检验统计值的绝对值 ||t大小——选择最小的一个剔除。剔除后重新构造回归模型，若仍有未通过t检验的变量，则继续按上述标准剔除相应的解释变量，重新构建模型——仿照原逐步回归的思想重复引入、剔除的步骤，直到没有变量被剔除、也没有变量被引入为此。实践证明，这种方法更简便，更清晰。下面以“中国经济增长的影响因素分析”为例，说明这一实现过程。

根据经济理论，影响经济增长的主要因素有投资、消费、进出口等，还有一些影响因素如价格指数、能源消耗量、汇率等。笔者收集到了1990～2009年各年度的宏观经济数据，它们是：国内生产总值（GDP）、居民消费支出（REC）、财政支出（GC）、固定资产投资（INV）、出口总额（TTR）以及能源消耗量（POWER）、汇率（EXC）、居民消费价格指数（CPI）等。为消除数据波动性和量纲不同的影响，将数据全部取自然底数对数，以ln(GDP)为被解释变量构建对数回归模型。

首先利用F检验下的逐步回归法构建出模型，这一步可以利用SPSS软件完成。逐步回归得到的最优模型为：

模型中的s和t分别是对应参数估计量的标准差和t检验统计量值。

下面以t检验方法对模型进行逐步回归。上述逐步回归过程设置引入变量的F临界值为3.84，剔除变量的F临界值为2.71，因此以t检验为准则的引入和剔除变量的临界值分别为tentry==1.96,tremoval==1.65，即当新引入的变量回归系数的t统计量绝对值在所有新引入变量中最大且大于tentry=1.96时，则引入该变量，否则不引入；当模型中存在回归系数的t统计量绝对值最小且小于tremoval=1.65时，则剔除该回归系数对应的变量。首先将所有变量引入模型运用EViews5.0估计模型参数得：

表1 1990～2009年中国部分宏观经济数据

为节省篇幅，模型只写出了t统计值。可以看出，汇率对数ln(EXC)的t检验统计量-1.16为最小，其绝对值小于1.65，因此剔除该变量，重新估计回归模型为：

显然在这一步要剔除的变量为ln(POWER)。接下来是引入先前已被剔除的变量ln(EXC)，引入后发现其t统计量绝对值仍是最小的，且小于剔除的临界值1.65，因此不予引入。这样构造的回归模型为：

该模型中应该剔除的变量为ln(TTR)。再继续引入已被剔除的模型，引入中发现，任一被剔除的变量重新被引入后仍是不显著的、需要再次剔除的变量。经过引入、剔除等步骤后（具体模型略），最终得到无须引入也无须剔除变量的模型是：

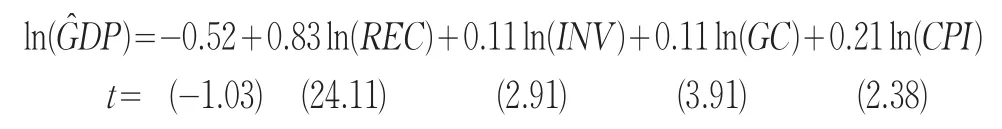
显然，这和F检验下的逐步回归结果是一致的，说明了在实际应用中运用t检验准则同样可以完成逐步回归。这个结果和经济理论中关于经济增长的三驾马车的论点是不一致的，即理论上认为影响经济增长的三大动力是消费、投资、进出口，而上述回归结果却显示中国经济增长未受到进出口的影响。这个结论显然有悖于现实，究其原因，是由于逐步回归计算过程的僵化——只通过所设置的临界值（或显著性水平）作为引入和剔除变量的唯一标准，而忽视了现实的经济理论。t检验的逐步回归虽然也存在同样问题，但它也具有灵活性，可以及时更改错误信息。本例中在进行t检验的逐步回归时就发现，进出口也是一个重要影响因素，当引入进出口后，须剔除变量ln(CPI)。模型构建如下：

其中ln(TTR)回归系数t检验的相伴概率仅为7.22%，相对较小。从各检验结果来看，该模型并无瑕疵,说明了影响GDP的主要因素有居民消费、政府消费、固定资产投资、进出口。其中居民消费的影响作用最大：居民消费每增加1个百分点，GDP平均增加0.79个百分点；进出口的影响作用最小：进出口每增加1个百分点，GDP平均增加0.04个百分点。从经济理论的角度来说，此模型比逐步回归所构造的模型更具说服力。因此，t检验下的逐步回归较F检验下的逐步回归更具灵活性。

4 结论

F检验和t检验是经典线性回归模型中两种重要的统计检验方法，根据文中所作研究可知，对逐步回归过程中引入或剔除变量的检验标准，可以使用t统计量，也可以构造F统计量进行F检验。论证发现这两种检验方法是等价的。但相比较而言，t检验更直观、便于理解，t统计量的计算较F统计量亦更简单。由于逐步回归中引入和剔除变量的依据是F检验，根据F检验和t检验的等价性，逐步回归同样可以使用t检验标准来完成，此时模型参数的求解方法仍使用“求解求逆紧凑变换法”。通常可借助于计算机来计算显著性检验t值，据此即可直接判定是否引入或剔除变量。通过研究中国经济增长的影响因素，在验证了t检验下的逐步回归可行性的同时还发现，传统的F检验下的逐步回归较为僵化，仅依据数字信息来判断是否引入或剔除变量，忽略了经济理论的指导作用，从而可能得出有悖于现实的结论。而基于t检验的逐步回归由于在每一步都需要构造模型，因而更易发现模型可能存在的问题，能结合实际理论对模型进行必要的修改和补充，更具灵活性。

[1] 周纪芗.实用回归分析方法[M].上海:上海科学技术出版社,1990.

[2] 伍德里奇.计量经济学导论:现代观点[M].北京:清华大学出版社,2007.

[3] 何晓群.应用回归分析[M].北京:中国人民大学出版社,2007.

[4] 陈希孺,倪国熙.数理统计学教程[M].合肥:中国科学技术大学出版社,2009.