多部门非线性经济系统的CGE模型构建

秦昌才

（1.对外经济贸易大学国际经济贸易学院，北京100029；2.烟台大学经济与工商管理学院，山东烟台264005）

一般均衡理论起源于瓦尔拉斯1874年的《纯粹经济学要义》，20世纪50年代阿罗、德布鲁从数学上严谨的证明一般均衡点的存在性、稳定性和唯一性，从而不断趋于成熟。如同一切科学的发展过程一样，一般均衡理论趋于成熟时必然走向实践，开辟应用领域，于是可计算一般均衡模型（简称CGE模型）于20世纪60年代开始出现。

瓦尔拉斯最先给出了市场供求平衡方程组的列写方法，因此他被公认为当代一般均衡分析的奠基人与开创者。虽然其非线性方程组的求解方法十分困难。但随着数学方法的不断完善和计算机技术的不断进步，可计算一般均衡理论与实践表明，瓦尔拉斯的模型构建思想是极为有用的。

本文将在瓦尔拉斯框架的基础上分析多部门非线性经济系统的一般均衡问题，以期为进一步解决多部门非线性动态经济系统的平衡增长和最优增长提供基本的CGE模型架构，而后者在经济学领域至今缺乏令人满意的研究结论与成果。

1 瓦尔拉斯一般均衡框架——以两部门为例

假设整个经济只有两种生产要素：资本K和劳动L，只生产两种不同的产品1和2，并且假设所有消费者具有相同的效用函数，即整个社会只有一个标准消费者。瓦尔拉斯均衡框架是依据利润最大化、效用最大化和供求平衡三原则建立起来的。

1.1 利润最大化原则

生产函数为：Qi=Q(Ki,Li)（i=1,2）

其中Qi为第i种商品的产出量，Ki,Li为生产第i种商品时的资本、劳动投入量，且函数满足：λQi=Q(λKi,λLi)，即规模收益不变。

假定劳动、资本的价格分别为w，r，第i种产品的价格为Pi，则第i部门的利润函数为：

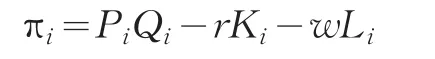
依据利润最大化原则：得产品i的供给函数为：

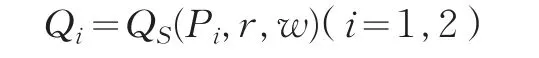
生产商品i对两种要素的需求函数为：

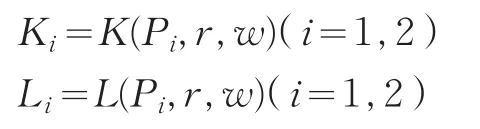
1.2 效用最大化原则

假设标准消费者的效用函数为：

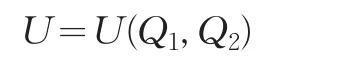
则消费者行为可由如下模型求解：

令拉格朗日函数为：

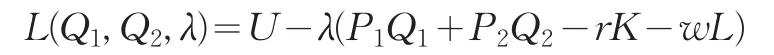
由

得消费者对第i种商品的需求函数为：

Qi=QD(Pi,r,w)

1.3 供求平衡原则

由产品市场出清得：由要素市场出清得：

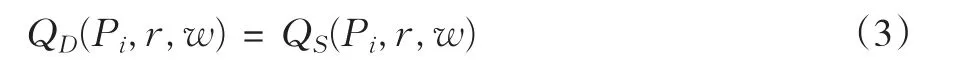
由（1）～（4）组成了 10个方程，共有 10个变量：K1,K2,L1,L2,Q1,Q2,P1,P2,r,w。

当然，n个方程n个变量并不意味着一定有解。但后来的经济学家阿罗和德布鲁证明了在最一般的情况下均衡解的存在性与唯一性问题。两人也因此获得了诺贝尔经济学奖。

2 柯布－道格拉斯经济特征

柯布－道格拉斯经济是最典型的经济形式，其消费者有着良好的偏好形状，生产者有良好的生产技术，效用函数和生产函数都是LES形式。

2.1 消费者偏好特征

任意一个消费者都拥有对数线性效用函数：

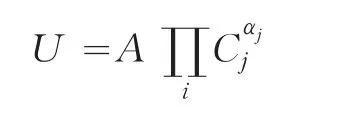
其中，Cj为消费者对第i种商品的最终消费量，αj为效用弹性系数，A为效用函数技术系数。

2.2 生产技术特征

第j种商品的生产函数为：

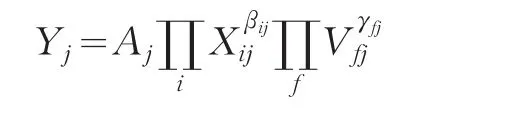
其中，Xij为第i种商品在生产第j种商品时的中间投入量，Vfj为第f种初始要素在生产第j种商品时的投入量，βij、γfj分别为产出弹性系数。

3 基于C-D经济的多要素、多部门的CGE模型构建

假设整个经济共有F种生产要素，供给量为Vf，（f=1,2…F），相应地，可以将消费者分为F类，共有N个部门（厂商）分别生产N种不同的产品。

3.1 产品供给函数与要素需求函数

由第j部门的生产函数为：

得其利润函数为：

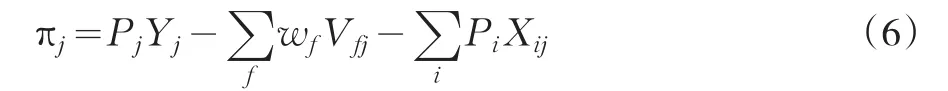
由（6）得：

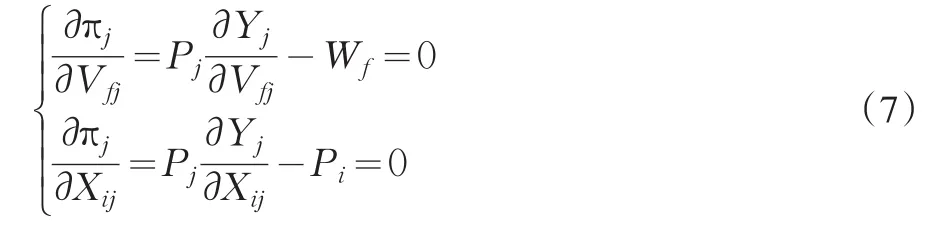
又由（5）得：

将（8）代入（7）得：

将（9）式代入（5）得：

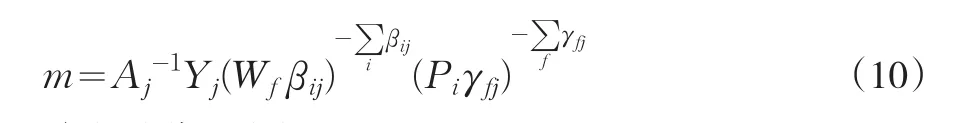
将（10）代入（9）整理得：

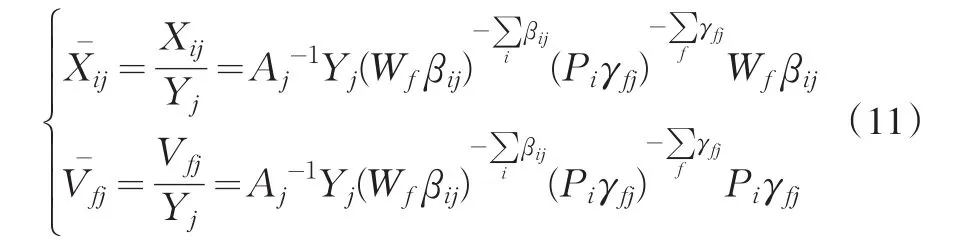
其中，、分别代表生产单位第j种商品所需的第i种商品和第f种初始要素禀赋的投入量，即是两种要素的需求函数。

则商品的成本定价方程为：

式（12）可以看成商品j的供给函数。因为它表明产品的合理定价应为式（12）右端。若实际价格比它高，市场供给量上升；如果实际价格比它低，该产品的市场供给量会下降至零。

3.2 消费者需求函数

第f个消费者的最优行为可由如下模型求解：

将（15）式代入（13）式的第二部分得：

这就是第f个消费者对第i种商品的需求函数。

3.3 供求均衡

由产品市场供求均衡得：由要素市场供求均衡得：

3.4 变量参数的估计

由（11）（12）（16）（17）（18）等组成的CGE模型方程组包含的参数可以分为两大类。

第一类：比率参数或称C－D函数参数，如αfj，γfj，βij，Aj等，都可以通过社会核算矩阵（SAM）来近似取得，如等。

第二类：均衡核心参数，如Yj,Wf,Pi等，由于计算量较大可通过GAMS等一般均衡的软件求得，而且这方面的软件技术已相当成熟。

4 结论

本文依据瓦尔拉斯一般均衡分析框架，分析基于柯布－道格拉斯经济的多要素多部门的可计算一般均衡模型的构建。这为多部门非线性经济系统的动态一般均衡分析提供了进一步分析的模型框架，将进一步拓展CGE模型在国际贸易、政府财政政策（特别是税收政策）、环境保护以及污染的外部效应、经济改革及发展政策、能源等领域之外的更多应用研究空间。

[1] Ian Sue Wing.Computable General Equilibrium Models and their Use in Economy-Wide Policy Analysis,MIT Joint Program on the Science and Policy of Global Change Technical Note No.6[Z].2004.

[2] Rutherford,T.F.Extensions of GAMS for Complementarity Problems Arising in Applied Economic Analysis[J].Journal of Economic Dynam⁃ics and Control,1995,19(8).

[3] Rutherford,T.F.Applied General Equilibrium Modeling with MPSGE as a GAMS Subsystem:An Overview of the Modeling Framework and Syntax[J].Computational Economics,1999,(14).

[4] Rutherford,T.F.,S.Paltsev.From an Input-Output Table to a General Equilibrium Model:Assessing the Excess Burden of Indirect Taxes in Russia,Mimeo[M].Colorado:University of Colorado,Boulder CO,1999.

[5] 程海芳等.CGE模型参数估计方法研究[J].武汉大学学报(工学版)，2003,（8）.

[6] 张金水.可计算非线性动态投入产出模型[M].北京：清华大学出版社，2000,（11）.

[7] 李洪心.生产者模型的求解与比较[J].财经问题研究，2005，（5）.