基于粒子群算法的导弹初始备件优化配置＊

宋贵宝 马广婷 刘学君 刘宗杰

（1.海军航空工程学院飞行器工程系 烟台 264001）（2.海军航空工程学院研究生管理大队 烟台 264001）

1 引言

备件的优化配置是装备保障的重要组成部分，它研究的主要问题是寻求备件费用与完好率之间的最佳平衡，最终合理确定备件的种类与数量。就其形式而言，备件优化问题可以看成是一个组合优化问题。组合优化问题是通过数学方法的研究去寻求离散事件的最优编排、分组、次序或筛选等问题。

近年来，受自然隐喻的启发，人们提出了各种各样的计算智能方法，如人工神经网络、遗传算法（GA）、蚁群优化算法（ACO）和粒子群优化算法（PSO）等等，它们广泛应用于各种困难的优化问题的求解，虽然不能保证获取最优解，但在问题规模较大时也能在可行时间内找到问题的满意解。粒子群优化算法具有并行处理、鲁棒性好等特点，与ACO算法类似，PSO算法是一种基于群智能方法的优化技术，同时与GA类似，是一种基于进化的优化工具。与GA比较，PSO算法的优势在于简单、易于实现同时又有深刻的智能背景，既适合科学研究，又特别适合工程应用。

本文提出了应用粒子群算法来解决备件优化问题的方法，在备件优化模型中，在费用和装备完好率共同约束下，解决装备完好率与备件费用之间的平衡问题。以粒子群算法为求解途径，得到最优配置。

2 备件优化模型建立

影响导弹备件优化配置的影响因素很多，例如导弹的战备完好率、有效度、费用约束、导弹使用环境等，但是主要是战备完好率和费用约束的要求。

为了便于理论研究和模型的建立，作如下假设：

1）备件的寿命服从泊松分布；

2）各备件发生故障的概率是互相独立的；

3）备件在存储过程中始终处于完好状态；

4）备件更换时间忽略不计。

2.1 导弹的战备完好率

战备完好性是指武器装备在使用环境下处于能执行任务的完好状态的程度或能力。取决于组成单元的完好性和系统的结构。导弹武器装备结构复杂，在拥有备件供应的条件下，其整个系统可以看作串联的“冷储备系统”。这里所谓的“冷储备系统”就是储备单元在储备期间不工作，且不会失效，其储备时间的长短对装备以后的使用没有影响。有些人认为装备的战备完好性越高越好，这忽略了费用的影响，显然是一种误解。

将战时导弹装备备件的消耗看做服从参数为λT的泊松分布［1］，其中，λ为某一部件的故障率，可根据具体作战想定或计算机模拟获得。T为作战持续时间。设装备由n个基本功能项目单元组成，第i种备件的故障率为λi，则其需要k个备件的概率为

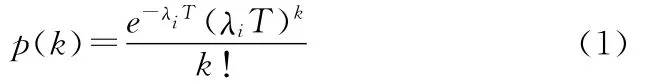
定义NNBOi为第i个备件的延期交货量［2］，设对应部件的库存量为Si，则

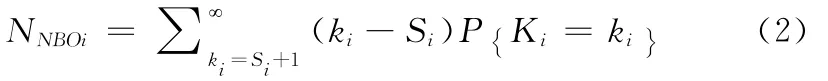
则导弹的战备完好率可表示为

图1 备件数与战备完好率的关系图

从式（3）中容易看出，战备完好率并非随着备件的增加而线形递增，部件可靠度与备件数之间的关系如图1所示。

当所求装备完好率A（S）大于或等于0.9时，可以认为该装备所有备件的携行数量为S＝（S1，S2，S3，…，Sn）时，可满足装备在作战期间的完好性。

2.2 保障费用

在导弹备件的配置中，其费用是重要的约束条件。费用太低，备件不足，无法发挥武器装备的性能；费用太高，耗费太大，不具有经济性。在装备保障过程中，备件保障费用主要由备件费、订货费、储存费、缺货费等组成，其中订货费就是订购备件时所需的手续费、电讯费、采购差旅费等，一般说订货费与订购次数有关而与订购备件数量关系不大；存储费包括备件占有资金的利息、运输费及由于技术进步而备件性能陈旧贬值所造成的损失费用等，存储费与备件的数量及存储时间有关；缺货费是指当备件供不应求时所造成的损失费用［3～4］。它们往往是与备件的数量成一定线性关系，为简化计算模型，备件的保障费用可表示为

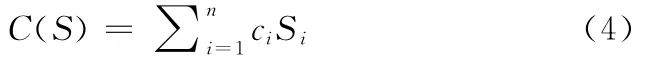
其中，ci为第i种备件的费用；Si表示第i种备件的备件数。

在装备保障的过程中，装备完好率和保障费用约束是必须考虑的问题［5～6］。在经费有限的情况下，达到一定的装备完好率是主要目标。在保证装备完好率和一定费用约束的前提下，为求得备件配置的最优化，本文建立以下模型：

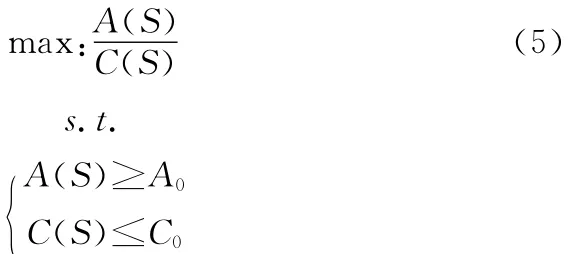
其中，C0为备件装备使用保障费用；A0为战备完好率的门槛值；s为备件数量矩阵。

3 粒子群算法

3.1 粒子群算法基本原理

粒子群优化算法，简称为PSO，是由Kennedy和Eberhart在1995年提出的一种基于群体智能的优化算法，是在鸟群和鱼群觅食行为规律的启发下上提出的［7］。

粒子群优化算法是基于群体智能理论的优化算法，通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索。与进化算法比较，PSO保留了基于种群的全局搜索策略，但是其采用的速度－位移模型操作简单，避免了复杂的遗传操作。它特有的记忆使其可以动态跟踪当前的搜索情况调整其搜索策略。与进化算法比较，粒子群算法是一种更高效的并行搜索算法。由于算法收敛速度快，设置参数少，近年来收到学术界的广泛重视。

PSO中，每个优化问题的解都是搜索空间中的一只鸟，称之为“粒子”［8］。所有的粒子都有一个由被优化的函数决定的适应值，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

对由n个粒子组成的群体对Q维（就是每个粒子的维数）空间进行搜索。每个粒子表示为：xi＝（xi1，xi2，xi3，…，xiQ），i＝1，2，3，…，n；每个粒子对应的速度可以表示为vi＝（vi1，vi2，vi3，…，viQ），i＝1，2，3，…，n；在每一次迭代中，粒子通过跟踪两个“极值”来更新自己：一是自己搜索到的历史最优值pi，pi＝（pi1，pi2，pi3，…，piQ），i＝1，2，3，…，n；二是全部粒子搜索到的最优值pg，pg＝（pg1，pg2，pg3，…，pgQ）。粒子群算法的位置更新按照公式（6～7）进行：

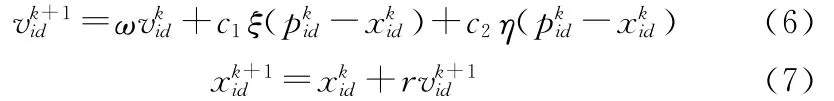
其中：i＝1，2，3，…，n，d＝1，2，3，…，Q，ω为惯性权重，c1、c2为权重系数，ξ、η为是介于［0，1］区间内均匀分布的随机数，r为约束因子，往往取1；为第i个粒子第k次迭代中位置的第d个分量，即为寻优配置；为第i个粒子第k次迭代中飞行速度的第d个分量，即为寻优路径；pid粒子i最好位置pi的第d个分量；pgd为群体最好位置pg的第d个分量。

3.2 适应度函数构造

根据初始备件模型，要求装备完好率与费用之比最大，同时满足，装备完好率大于0.9，费用小于C0。因此这是一个有约束条件的优化问题，对于不等式约束，传统处理方式为采用罚函数［9］，可以把原约束方程作为罚函数项加入到适应度函数中，变成无约束的优化问题，适应度函数构造如下：

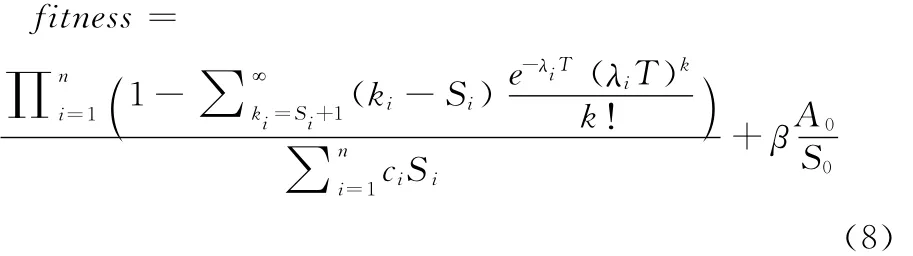
式中β为惩罚参数，需要保证惩罚函数与原适应度函数处于同一个数量级。

3.3 模型求解

粒子群算法的求解过程如图2所示。如图1所示，粒子群算法步骤如下：

1）初始化群体微粒（群体规模为N），包括随机位置和速度，并将每个粒子的原始位置设置为，原始速度设置为；

2）求出每个粒子的适应值（fitness value）；

3）对每个微粒，将其适应值与其经过的最好位置xi（pi）时的适应值作比较，如果较好，则将其作为当前的最好位置xi（pi）；

4）根据公式（1）、（2）更新微粒的速度和位置；

5）检查各变量是否溢出各自的取值范围。若某一变量越限，则取其相应的限值，以防止粒子超出可行的搜索区域。

6）根据终止条件判定是否终止迭代。达到最大允许迭代次数或相邻若干次迭代中适应值变化小于设定值，停止优化并输出结果；否则，迭代次数加1并返回（2）继续迭代。

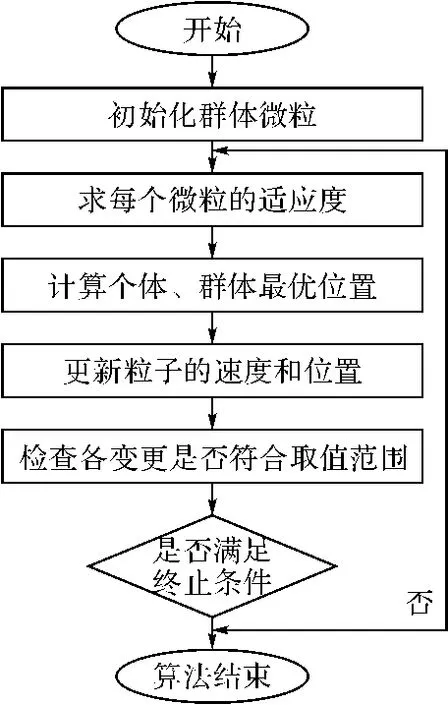
图2 粒子群算法步骤

4 案例分析

假设某型导弹上有四种类型的主要备件，其对应的备件单价和故障率如表1所示：

表1 备件参数表

其中费用最高为300，000元，装备完好率门槛值为0.9。

在用粒子群算法解决此问题时，单个部件数取值为1～20的正整数，粒子速度向量最大值vmax设定为1，即v∈［－1，1］，经过试验，惯性权重ω取值为1.05，加速度系数c1，c2取2，PSO群体规模取20，最大迭代次数取120。

粒子群算法在50步左右找到最优解，即适应度函数值fitness为5.49083E－06，最优配置pg＝［9，7，5，1］T，装备总费用为173，850，装备完好率为0.95458。与遗传算法相比，能更快的收敛于最优解，提高工作效率。

5 结语

备件优化不仅可以保证装备战备完好率，并且也是减少备件费用浪费的重要手段［12］。本文应用粒子群算法来解决初始备件优化问题，建立了备件优化模型，在费用和装备完好率共同约束下，以寻求装备完好率与费用最大比值的初始备件优化模型，利用粒子群算法的算法简单、收敛速度快、需要调整参数少，全局寻优能力强的特点，得到装备初始备件的最优配置。通过对某型导弹的初始备件的优化计算，证明粒子群算法能较好的解决导弹装备初始备件的优化问题。

［1］孙洪祥.随机过程［M］.北京：机械工业出版社，2008：132－136.

［2］刘喜春，郑华，仲辉，等.备件配置优化问题研究［J］.系统工程与电子技术，2008，30（10）：1934－1937.

［3］钱平.维修工程基础［M］.三原：空军导弹学院，1990.

［4］陈学楚.装备系统工程［M］.北京：国防工业出版社，1995.

［5］肖波平，康锐，王乃超.民机初始备件方案的优化［J］.2010，36（01）.

［6］李薇，林干.地空导弹武器系统备件需求模型［J］.2010，31（01）.

［7］J.Kennedy，R.Eberhart，Particle swarm optimization［C］.Proc.IEEE Int.Conf.on Neural Networks，Perth，Australia，1995：1942－1948.

［8］冯雪，裴志松.粒子群优化算法的研究与应用［J］.2011，28（03）.

［9］丁玉凤，文劲宇.基于改进PSO算法的电力系统无攻优化研究［J］.2005，33（6）：20－24.

［10］瞿勇，栾兵，宋业新.基于粒子群优化的混合模糊双矩阵对策求解［J］.计算机与数字工程，2010（11）.

［11］刘家骏.基于粒子群优化算法的系统可靠性优化［J］.计算机与数字工程，2012（4）.

［12］连翠萍，刘喜春，李群，等.基于仿真优化的飞机维修备件优化问题研究［J］.2006，23（10）.