基于层次分析法模型的航空兵进攻作战效能分析*
侯岳海
(军事科学院研究生部 北京 100091)
1 引言
由于航空兵进攻作战计划和任务的确定要求较高,需要对战前的各种战术战役情报、自然条件、己方装备实际状态等因素进行综合性考虑,作战效能的评估分析,不仅可以应用于战前的筹划而且可以应用于战后针对实际结果进行综合统计评估。但在综合各种因素时判断性选择和定性分析占相当大的比重,缺乏数学方法的定量分析,这与作战系统所需的科学方法体系存在一定程度的矛盾性,因此结果的不确定因素和准确性难以保证。本文通过层次分析法对航空兵作战效能进行定量与定性相结合的相关分析。
2 层次分析法的概念和具体步骤[1~4]
层次分析法(AHP)是一种实用的多方案或多目标的决策方法。其合理地将定性与定量的决策结合起来,按照思维的规律把决策过程层次化、数量化。具体步骤如下:
2.1 明确问题
在分析问题时,首先要对问题有明确的认识,弄清问题的范围,了解问题所包含的因素,确定出因素之间的关联和隶属关系。
2.2 递阶层次结构的建立
根据对问题分析和了解,将问题所包含的因素,按照是否共有某些特征进行归纳成组,并把它们之间的共同特性看成是系统中新的层次中的一些因素,而这些因素本身也按照另外的特性组合起来,形成更高层次的因素,直到最终形成单一的最高层次因素。
2.3 建立两两比较的判断矩阵
判断矩阵表示针对上一层次某元素,本层次各元素与其之间相对重要性的比较,一般取如下形式(见表1):

表1 判断矩阵表
判断矩阵中的ωi/ωj是根据资料数据、专家意见和系分析人员经验经过反复研究后确定。
在层次分析法中,为了使判断定量化,关键在于设法使任意两个方案对于某一准则的相对优越程度得到定量描述。一般对单一准则来说,两个方案进行比较总能判断出优劣,层次分析法采用1~9标度方法,给出数量标度。(见表2)
2.4 层次单排序
层次单排序是通过计算判断矩阵的特征值和特征向量而得,其中所求得的特征向量的各元素即为所要求的对应元素单排序的权值,亦即对判断矩阵B,计算满足BW=λmax的特征值和特征向量,其中λmax为B的最大特征根,W为对应的正规化向量,而W中的各W(i)即作为对应元素相应单排序的权值。
也就是说,层次单排序就是把本层所有各元素对上一层来说,排出评比顺序,对于计算判断矩阵的最大特征向量,常用方法是方根法和和积法。(本文采用方根法)计算步骤如下:

表2 判断矩阵数量标度
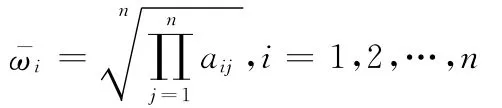
1)计算判断矩阵每行所有元素的几何平均值:
2)将归一化:
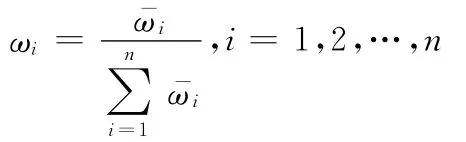
得到各因素的相对权重ω=(ω1,ω2,…,ωn)T。
3)计算判断矩阵的最大特征根λmax:
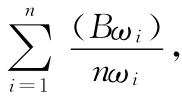
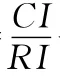

表3 RI值表
2.5 层次综合排序
利用单排序的计算结果,进一步综合出对更上一层次的优劣顺序,对结果进行整体排序。
3 算例分析
本文对航空兵进攻作战效能的分析从情报、气象、装备因素以及其子因素[5~6]进行综合评估,利用AHP对若干作战单元进行分析。
情报因素(敌方)主要考虑敌方装备、区域状态、兵力部署以及其它因素。
1)敌方装备主要考虑敌方装备的具体战术性能参数以及装备目前的状态、数量等。
2)区域状态主要考虑距离、地形地貌等因素。
3)兵力部署主要考虑兵力数量实力、分布结构密度、敌干扰强度、防御状态等。
4)其它因素考虑周边社情、有无其它军事力量干预以及后续行动情况等。
气象因素取允许飞行的最低气象条件主要取决于云端高低、风力情况、能见度[7]。其取值大小要根据各因素对飞行的有利程度来确定。云端越高、能见度越好、风力情况越好(如侧风风速较小,地区气象气压较为稳定等)取值越大;反之取值越小。
装备因素(己方)主要考虑性能状态、火力效能、数量规模、保障条件四项[8],各项因素取值越大即反应装备越优良,越利于作战任务的实施;反之取值越小则说明装备状况越不利于作战或作战任务完成的较为困难。
5)性能状态依据列装装备的具体战术性能参数、使用强度以及装备目前的状态[9]。
6)火力效能依据装备可使用的武器弹药状态参数以及可用条件。
7)数量规模通常按照数量规模越大取值越多来确定。
8)保障条件依据己方保障能力、实际保障状态以及战损恢复能力等。
3.1 航空兵进攻作战效能体系的确定
根据上述各因素可以确定如下评估体系:(选取三个不同情况的作战单元作为备选对象)
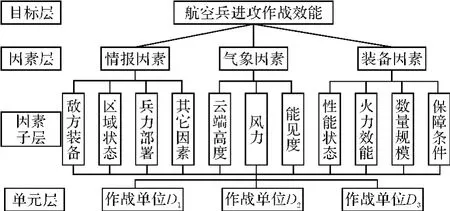
图1 航空兵进攻作战效能体系图
3.2 因素层在目标层权重的确立
就各因素在目标层下进行两两比较得到相应矩阵,利用法求得判断矩阵的特征值和相对应的特征向量(即权重分布),并且检验一致性。(见表4)

表4 因素层权重分布矩阵
即得判断矩阵


各因素的权重ω是(0.238,0.626,0.136)
同理可得各子因素相对于因素评定值分别为


各子因素的权重ω1是(0.106,0.327,0.124,0.443);

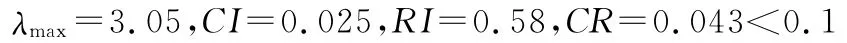
各子因素的权重ω2是(0.184,0.231,0.585);

3.3 单元层相对与因素层权重的确定
将三个作战单位D1,D2,D3做相应的评定(方法同上)


则对应权重是

依据综合分析评估结果公式
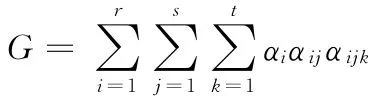
其中α是各层之间的权重值,t是案例数,是r因素个数,s是因素下子因素个数。
即可判断出各值:

该方法为行动计划提供了优先排序,在本算例中经过计算作战单元D2的结果值最高,可以优先考虑选用作战单元D2。
在军事行动计划中,可以根据实际情况来综合选择相关因素的种类和数量,以选取的考虑因素来构建分析层次架构;对建立的实际分析体系可借助计算机来完成分析计算;同时可以根据各级评价矩阵来具体分析实际情况的量化标准,以求计划方案的科学性和对此安排的精细保证。同时此方法还可以用于对已执行的行动进行科学评估,特别是对作战中不同因素间分析,可利用所构建的层次架构进行量化比较,较为准确的评估作战因素的作用和影响,使对相关因素的评估不仅仅停留在主观定性层面,同时能够具体量化因素对行动的影响程度,为后续行动的优化和实际数据的统计提供了可靠的工具。
4 结语
现代军事行动中对于任务的详细制定和完成情况的评估都要考虑大量的因素[11],因其完成结果具有重要意义和价值,故对于军事行动的科学性和合理性要求很高。本文基于层次分析法的特点,提出了一种适用于航空兵进攻作战行动的分析方法,通过是实例的分析,证明了该方法的合理性,为军事行动方案提供了定性定量相结合的科学手段。
同时该方法也存在一定的局限性,其只能在已有方案中选优,不能自生备选方案。考虑各因素也只能是在有基础上进行分析,对于不确定因素的考虑不够全面,有待进一步完善和改进。
[1]姜启源.数学模型[M].第2版.北京:高等教育出版社,1998(10):16-22.
[2]许志国.系统科学[M].上海:上海科技教育出版社,2000,9:7-12.
[3]周赤非.新编军事运筹学[M].北京:军事科学出版社,2010,1:32-35.
[4]《运筹学》教材编写组.运筹学[M].第3版.北京:清华大学出版社,2005,6:455-460.
[5]刘斌,等.空地作战指控系统效能评估仿真研究[J].计算机仿真,2011(5):38-42.
[6]孔祥忠.战场态势估计和威胁估计[J].火力与指挥控制,2003(12):91-98.
[7]章澄昌.飞行气象学[M].北京:气象出版社,2000(8):8-37.
[8]王锐.先进战斗机作战效能评估[D].西安:西北工业大学,2007:34-38.
[9]张考,马东立.军用飞机生存力与隐身设计[M].北京:国防工业出版社,2002,6:1-14.
[10]杨杉,曹波.层次分析法在电网信息系统安全评估分析中的应用[J].计算机与数字工程,2011(10).
[11]江敬灼,叶雄兵.军事系统复杂性分析以及启示[J].军事运筹与系统工程,2007,21(4):26-30.

