舰艇编队对敌海上编队导弹攻击火力分配的GA算法研究＊

古军峰 郭定荣 贾 π

（1.海军蚌埠士官学校信息系统教研室 蚌埠 233012）（2.海司信息化部 北京 100000）

1 引言

现代海战中，交战的敌我双方基本上都会采用编队作战的方式进行对抗。我军水面舰艇编队主要以导弹艇编队、导弹驱护舰编队和导弹驱逐舰、导弹艇合成编队对敌进行编队作战。敌水面舰艇编队在很大程度上将会是一个将各有所长的水面舰艇组合起来的构成具有多功能、多层次、全方位、大范围的海上攻防作战系统，其出现形式可能为一个具有数量众多的水面舰艇组成的大编队。在这种作战样式下，舰艇编队用何种类型导弹打击敌编队的何种舰艇，以及导弹攻击时所需要分配的导弹数量，成为现代舰艇编队对敌作战需要迫切解决的问题。合理的运用己方的舰舰导弹武器进行战术决策，达到最大的对敌作战效果，同时又最大程度的保存己方实力，是导弹攻击火力分配问题所追求的目标。

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。它利用目标函数的取值信息，无需梯度等高阶信息，因而适应于大规模、高度非线性的不连续多峰函数的优化以及无解析表达式的目标函数的优化问题。并且它还具有良好的并行性、全局优化性能和稳健型。所以我们用它来解决舰艇导弹攻击的火力分配问题。

2 舰艇编队导弹攻击火力分配

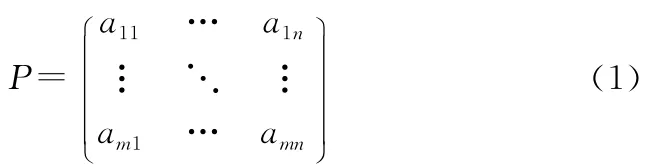
式中，aij表示第i种导弹分配给第j艘敌舰艇的导弹数量。

舰艇编队舰舰导弹攻击火力分配问题，实际上也是一个典型的最优化问题。评价火力分配方案打击效果优劣的原则有多个，主要思想就是打击效果最大、自我消耗最小等［5］。

2.1 敌方毁伤最大原则

对于特定的敌编队，假设我编队舰舰导弹攻击火力分配方案已定。设用第i艘舰艇舰舰导弹射击第j个目标时，第i艘舰艇单发导弹对第j个目标的毁伤概率为rij。若发射导弹数量为aij，则毁伤目标的概率为

m艘舰艇发射导弹对目标j的毁伤概率为（假设各枚导弹毁伤概率是弱相关的）：

最优火力分配的目标函数之一，是使对整个敌舰艇编队的毁伤概率达到最大，也就是使毁伤目标数的数学期望达到最大。于是，总的毁伤概率最优化的目标函数为

同时应当满足下列约束条件：

2.2 战略战术价值最大原则

符合作战使命的程度：编队作战中，有的舰艇以打击大中型水面舰船为其使命任务，有的舰艇以打击中小型水面舰艇为其使命任务，所以符合作战任务的程度是舰艇编队导弹攻击作战使命的一个重要因素。设敌舰艇编队各舰艇符合我作战使命的向量为

·敌目标价值系数：考虑到敌各个目标的不同特性和不同战术价值的、以及目标的造价等等因素，敌目标价值系数也是评价打击效果的一个重要指标。

·敌目标威胁程度：目标舰艇对攻击方的威胁程度各有不同，威胁程度主要取决于对攻击方毁伤概率的大小和毁伤发生的早晚。一般情况下，对威胁大的目标，应该首先实施强度较大的攻击，以确保攻击方之安全。

·敌目标的易于攻击性：目标舰艇相对攻击者的战术态势（指距离、方位、舷角），对攻击是否易于奏效有明显影响。如：是否处于孤立无援状态，是否在编队中处于突出或边缘位置，是否处于机动受限的状态，是否处于复杂环境中，等等。目标对舰舰导弹的防御能力，也是影响导弹攻击能否奏效的重要因素。一般应首先选择易于攻击、易于奏效的目标。

综合以上原则，我们可以得到敌目标战略战术价值向量K：

2.3 我方消耗最小原则

舰艇舰舰导弹的造价一般都比较昂贵，合理的利用舰舰导弹，使其以最小的代价来取得最大的打击效果也是舰舰导弹攻击火力分配所追求的一个目标。

设我舰艇编队舰舰导弹的价值向量F＝（f1，f2，…，fm），舰舰导弹消耗向量为C＝（c1，c2，…，cm），则我方最终消耗价值优化函数为

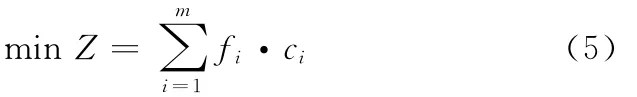
2.4 综合评价函数

综合以上原则，我们最终可以得到综合评价函数

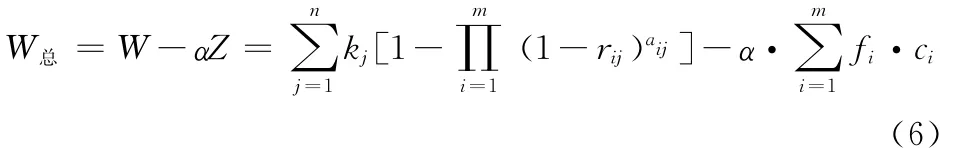
式中，α为原则偏重修正系数，同时也起到平衡量纲的作用，一般为一经验数值。

3 遗传算法设计

3.1 遗传编码

为了实现舰舰导弹火力分配的遗传算法计算，我们对导弹攻击火力分配向量P进行编码，即把第i艘舰艇对敌方j舰艇的分配数量aij当做自变量。首先，我们把我方每艘舰艇对敌方各艘舰艇舰艇导弹攻击的数量作为基本单元进行初始编码；然后，把初始编码转化为二进制编码。考虑到二进制编码一些局限性（二进制编码不便于反映所求问题的结构特征，比如，对于一些连续函数的优化问题等；另外，由于遗传算法的随机特性而使得其局部搜索能力较差）为改进这些特性，本文使用格雷码编码方法。

格雷码有这样一个特点：任意两个整数的差是这两个整数所对应的格雷码之间的海明距离。其连续的两个整数多对应的编码值之间仅仅只有一个码位是不相同的，其余码位都完全相同。使用格雷码来对个体进行编码，则编码串之间的一位差异，对应的参数值也只是微小的差别。这样就相当于增强了遗传算法的局部搜索能力，便于对连续函数进行局部空间搜索。

假如有一个二进制编码为B＝bmbm－1…b2b1，其对应的格雷码为G＝gmgm－1…g2g1。由二进制编码到格雷码的转换公式为

由格雷码到二进制码的转换公式为

3.2 适应度函数

本文最终对舰舰导弹攻击火力分配方案的评价函数是一个最大化问题的函数，即求

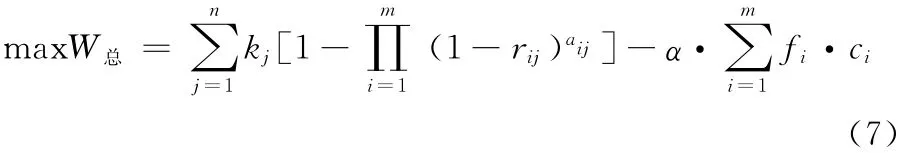
式中，cmin设定为当前所有代或最近K代中g（x）的最小值。

3.3 遗传算子设计

3.3.1 选择算子

选用适应值比例选择。这种方式首先计算每个个体的适应值，然后计算出此适应值在群体适应值总和中所占的比例，表示该个体在选择过程中被选中的概率。选择过程

对于最大化问题，一般采用下述方法：体现了生物进化过程中“适者生存，优胜劣汰”的思想，并且保证优良基因遗传给下一代。

对于给定的规模为n的群体，个体ai的适应值为f（ai），其选择概率［3］为

3.3.2 交叉算子

以一致交叉作为交叉算子。一致交叉即染色体位串上的每一位按相同概率进行随机均匀交叉。一致交叉算子生成的新个体为［3］：s′1＝a′11a′12…a′1L，s′2＝a′21a′22…a′2L，操作描述如下：

式中，x是取值为［0，1］上的负荷均匀分布的随机变量。

3.3.3 变异算子

为提高遗传算法对重点搜索区域的局部搜索性能，采用高斯变异。所谓高斯变异操作是指进行变异操作时，用符合均值为μ、方差为σ2的正态分布的一个随机数来替换原有基因值。由正态分布的特性可知，高斯变异也是重点搜索原个体附近的某个局部区域。

在进行由s＝a1a2…ak…aL向s′＝a1a2…a′k…aL的变异操作时，若变异点ak处的基因值取值范围［］，并假设［6］：

则新的基因值x′k由下式确定：

式中，ri为［0，1］区间一均匀随机数。

3.4 运行参数的确定

编码串的长度l：根据前面的编码方法，可得到编码串长度l＝4×m×n。其中，m为我方舰艇的数量，n为敌方舰艇的数量。例如，编队海上作战中，我方舰艇数量为12艘，敌方舰艇数量为15艘，则编码串的长度为720位二进制编码。

群体大小M：综合考虑遗传算法的运行速度和群体的多样性，本文设定群体规模为50。

交叉概率Pc：为了不影响群体的优良模式，本文交叉概率不选用较大的值，本文选用0.5作为遗传算法的交叉概率。

变异概率pm：变异操作是保持群体多样性的有效手段本文取0.005。

终止代数T：终止代数是表示遗传算法运行结束条件的一个参数，它表示遗传算法运行到指定的进化代数之后就停止运行，并将当前群体中的最佳个体作为索求问题的最优解输出，取1500。

4 结语

文中首先分析了影响舰艇编队舰舰导弹火力分配的主客观因素，建立了评判火力分配问题的数学模型，运用遗传算法对此数学模型进行优化求解设计。大量仿真试验表明，在敌我双方编队规模较大的情况下，遗传算法在求解此问题时，一般在900～1200代就能达到收敛，较之其它方法更容易获得客观的评价结果，有比较好的实时性。并且，试验过程中通过灵敏度分析，找到了影响舰艇编队导弹攻击火力分配的主要因素。这些，对我们以后进行的舰舰导弹火力分配研究都将起到很重要的作用。

［1］Cerf R.Asymptotic Convergence of genetic algorithms.Adv Appl Prob，1998.

［2］Goldberg D E.Genetic algorithms in search，optimization and machine learning.New York：Addiso－Wesley Publishing company，1989.

［3］周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999，6：45－70.

［4］李敏强.遗传算法的基本理论与应用［M］.北京：科学出版社，2002，3.

［5］李晓阳，方立恭.舰舰导弹作战运筹分析［M］.海军大连舰艇学院，2002，6：32－36.

［6］毕义明.遗传算法及其军事应用［M］.北京：解放军出版社，1998，8：44－51.

［7］金鸿章，王科俊.遗传算法理论及其在船舶横摇运动控制中的运用［M］.哈尔滨：哈尔滨工程大学出版社，2007.

［8］张文修，梁怡.遗传算法的数学基础［M］.西安：西安交通大学出版社，2000，1.

［9］王小平，曹立明.遗传算法—理论、应用与软件实现［M］.西安：西安交通大学出版社，2002，1.

［10］吴平健，李智勇.目标分配的遗传算法改进研究［J］.计算机与数字工程，2009，37（9）.

［11］姚跃亭，赵建军，尹波波，等.舰艇编队防空目标分配优化算法研究 ［J］.计算机与数字工程，2011，39（1）.

［12］肖支才，程春华.基于改进遗传算法的反舰导弹协同任务规划［J］.计算机与数字工程，2010，38（5）.

［13］［英］米凯利维兹.演化程序—遗传算法和数据编码的结合［M］.北京：科学出版社，2000，1.