粗糙集理论在装备故障诊断中的应用

张光轶，苏艳琴，许爱强

(1.海军航空工程学院研究生管理大队，山东 烟台 264001;2.海军航空工程学院科研部，山东 烟台 264001)

粗糙集理论在装备故障诊断中的应用

张光轶1，2，苏艳琴1，许爱强2

(1.海军航空工程学院研究生管理大队，山东 烟台 264001;2.海军航空工程学院科研部，山东 烟台 264001)

针对目前部队的装备故障诊断能力较弱的现状，通过几种故障诊断方法的比较，选取出粗糙集作为装备故障诊断方法，从而对已得到的装备状态的测试数据进行分析，利用粗糙集的约简算法消除冗余信息，利用决策表的形式从不完备的、不精确的测试数据中导出诊断规则，并应用于某型电台装备中进行故障诊断。结果表明，诊断结果快速准确，为今后进一步研究粗糙集算法在故障诊断中应用提供了依据。

故障诊断;粗糙集;电台装备

0 引言

装备是军队战斗力生成的重要组成部分，装备的保障成为保持、恢复和提高战斗力的重要因素，其中装备的维修性保障是装备综合保障工作中不可或缺的一部分，历来受到各国军队装备保障人员的重视［1］。装备使用中的维修主要分为修复性维修、预防性维修、改进型维修和战场抢修［2］。其中，故障诊断作为一种典型的修复性维修工作，长期以来，我军主要是依靠使用和维修人员的经验和知识对零部件故障进行诊断，对维护人员的文化程度和工作经验的依赖性较高;另外，虽然近年海军部队已经装备了大量自动测试设备，部队的维修保障水平已有了较大提高，大量的装备状态的测试数据，但其中存在着大量的冗余信息和多数测试设备仅能完成功能、性能检查，故障诊断能力较弱，因此研究装备故障诊断技术对提高部队深层次的维修保障能力具有很强的现实意义。本文将粗糙集理论应用到装备故障诊断中，就是利用其属性约简算法对消除冗余信息的优势［3］，且能以决策表作为工具，直接从不完备的和不精确的测试数据(故障数据库)中推导出故障诊断规则［4］，确定故障类型及故障模式对装备的影响，从而为准确地故障诊断，确保装备的可靠性和维修性提供了一种技术途径，具有一定的军事研究价值。

1 粗糙集理论及其应用优势

1.1 粗糙集基本理论

粗糙集理论是波兰科学家Pawlak和来自波兰科学院、华沙大学的一批逻辑学家于20世纪70年代，在研究信息系统逻辑特性的基础上发展起来的。1982年，Pawlak总结了前面的研究成果，发表了经典论文［5］，标志着粗糙集理论的正式诞生。

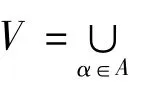
1.2 粗糙集中的关键技术

粗糙集理论应用中的关键技术主要包括粗糙集的离散化算法、属性约简算法和值约简算法等。

一般而言，故障数据库中的属性可分为连续(也成为定量)属性和离散(定性)属性。由于粗糙集理论主要是针对离散数据进行决策，因此用粗糙集理论处理连续的故障数据时，必然要首先进行数据离散化。考虑到能处理电子元器件参数漂移数据，提高诊断的可靠性，本文使用了经典的精确离散化方法，即在操作属性的变化范围内产生一系列属性值或“切点”，相邻切点构成的区间作为连续属性值的离散依据［6］。

属性约简就是在不影响原来系统分类的情况下，删除不相关或不重要的条件属性，使原有的系统得到简化。目前，获取属性约简的方法有很多，但无论什么方法，对于约简算法的最终目的都是一样的，即追求属性约简算法具有较佳的有效性和较高的运算效率。经典的粗糙集约简算法有基于属性重要度、差别矩阵、差别函数、信息熵、遗传算法的约简算法等［7］。

1.3 粗糙集在装备故障诊断中的应用分析

将粗糙集理论从大量故障数据中发现隐含的知识，揭示潜在的规律，确定诊断规则，粗糙集在装备的故障诊断中应用具有以下优势:一是粗糙集理论建立在不可分辨关系的基础之上，由此而衍生的一系列方法在数学上非常严密。从而得到的诊断决策表经得起推敲，提高装备故障诊断的可靠性;二是粗糙集方法可以找出数据中隐含的内在关系，并能对数据的意义做出评估，具有其他方法不可替代的作用。这一点对于装备故障诊断尤为重要，因为很多故障的产生都具有衍生性，一个故障有可能会引发新的故障，产生串联反应，粗糙集恰能从中寻找出这些故障间的关系，为最终判定故障根源提供依据;三是粗糙集的属性约简算法能对不影响诊断结果的多余条件属性进行删除，从而简化诊断结果，提高诊断效率;四是粗糙集完全由数据驱动，在应用时，无需提供除问题所需处理的数据集合之外的任何先验信息;五是粗糙集能表达和处理不完备信息，能在保留关键信息的前提下对数据进行化简并求得知识的最小表达，并能从中获取易于证实的规则。而装备测试数据往往存在着空值、噪声等大量不完备和不精确的信息，因此开展粗糙集理论在装备故障诊断中应用很有意义。

2 粗糙集在装备故障诊断中的应用方案

将粗糙集理论应用于装备故障诊断时，首先面对的就是待诊断故障数据库(各种测试数据)。这里，首先需对连续的测试数据进行离散化处理，采用设定测试数据门限区间值的精确离散化算法;然后，在保持决策属性和条件属性之间依赖关系不发生变换的前提下，对原始决策表约简。本文采用基于条件熵的约简算法，根据约简得到的新决策表生成诊断决策表规则;最后输出故障诊断，如图1所示。

图1 基于粗糙集的故障诊断流程图Fig.1 The flowchart of fault diagnosis based on rough set theory

基于条件熵的属性约简算法步骤可以概括为:Input决策表S=(U，A，V，f)，其中A=C∪D;Output决策表的1个最小约简REDC(D)。

步骤1 假设决策属性D在论域U上的划分为D:D={D1，D2，…，Dm}，计算决策表S中决策属性集D相对条件属性C的条件熵

其中，P(Ci)为条件属性Ci的概率;P(Dj|Ci)和P(Ci|Dj)分别为条件概率;

步骤2 计算条件属性C相对于决策属性D的核CORED(C)，令Att=C－CORED(C);

步骤3 令RED=CORED(C)，对每个属性αi∈Att，计算H(D|RED∪ {αi});

步骤4 选择使H(D|RED∪{αi})最小的属性αj，若同时有多个属性达到最小值，则从中选取1个在差别矩阵中出现最多的属性。令Att=Att－{αj}，RED=RED∪{αj}，计算H(D|RED)，若H(D|RED)=H(D|C)则终止，否则转步骤3。

3 应用算例

某型短波通信电台是装备我军新一代主战舰艇的通信设备，由于其长期处在各种海洋、电磁环境的应力下，经常出现故障。本文将粗糙集应用于该型电台的故障诊断中，故障定位到芯片级。整个电台由前面板模块、微机模块、频综模块、主接收机模块、救生接收机模块、解扩解调模块、同步模块、激励模块和功放模块9个模块构成，每个模块涉及电压、电流、功耗、频率等测试值［8］。每一模块出现故障其征兆表现为，相关测试性能指标超出标称值范围，即所谓的测试项目超差。这里，选取电台不受控制这一常见故障进行诊断。当这一故障出现时，+5V电压、UUT收信端电压、UUT收信端功耗、UUT发信端电压、UUT发信端功耗和通信总线参数都可能有异常出现，如图2所示。对10次故障测试的样本进行分析，表1给出相关测试项目与离散化结果(电压单位V，功耗单位W，总线单位ms)。其中，各测试项目采用精确离散化的门限也已在表1给出，超出这一区间则定义为“1”，表示“异常”;包含于这一区间则定义为“0”，表示“正常”。经过精确离散化后，还需经过数据预处理:①进行条件属性简化，即从原始决策表中消去在所选的故障中没有变化的行;② 消去重复列，因为重复行表示重复的样本，即同样的决策，所以可以消去，从而得到离散化结果与“前面板模块”和“主控微机模块”测试故障现象的对应关系，并按决策属性重新排列，得原始决策表(见表2)。

图2 电台不受控制的故障关系图Fig.2 The fault relationship of uncontrolled radio

?

?

通过第2节给出的基于条件熵的约简算法进行下列计算:

1)计算原始决策表中的决策属性集D相对条件属性C的条件熵H(D|C)=0，可见本例为一致性决策系统。

2)依次标注各属性为1～6，计算得原始决策表的差别矩阵为:

另外，可得原始决策表的相对核为CORED(C)={1，2，6}，令Att=C－CORED(C)={3，4，5}。

3)令RED=CORED(C)={1，2，6}，对每个属性{3，4，5}分别计算H(D|RED∪{αi})得:

4)可得Att=Att－{4}={3，5}，RED=RED∪{αj}={1，2，4，6}。经计算H(D|RED)=H(D|C)=0，至此运算结束。

根据约简算法得新决策表如表3所示。将新决策表添加到诊断系统的规则表，如表4所示。

?

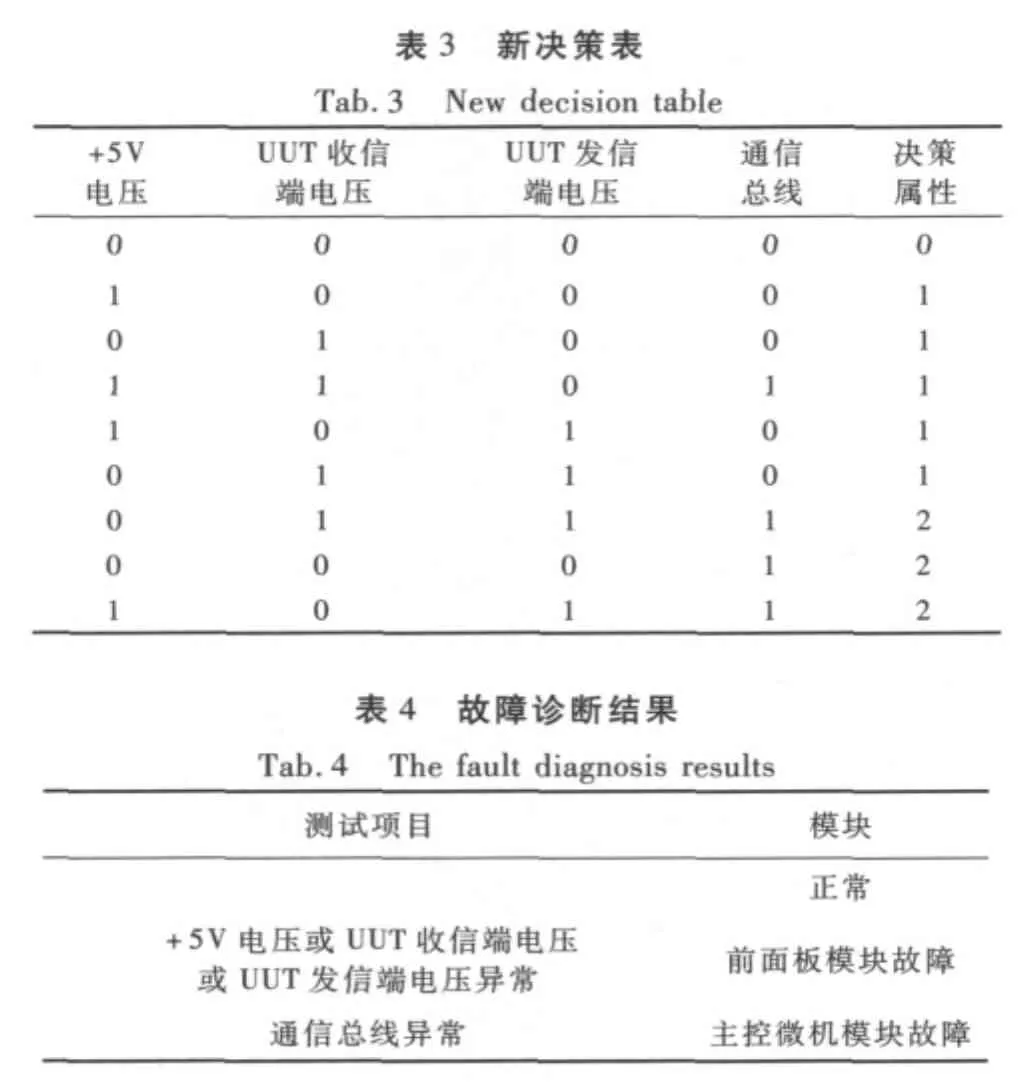
经原理分析与电路实测检验，诊断结果与实际情况相符。

4 结语

本文从对装备故障诊断对部队保障工作的重要性分析开始，选取粗糙集作为一种适合的故障诊断方法;并对粗糙集的基本理论及其离散化和属性约简算法进行介绍，从而对粗糙集应用于装备故障诊断的关键问题进行分析;得出粗糙集在装备故障诊断领域极具应用优势，并应用于某型电台装备的故障诊断中得出约简的故障诊断结果，并且准确快速，从而为部队提高装备的可靠性和维修性提供了一种技术途径。

［1］徐宗昌.装备保障性工程与管理［M］.北京:国防工业出版社，2006.12 －36.

XU Zong-chang.Equipment support of engineering and management［M］.Beijing:National Defense Industry Press，2006.12 －36.

［2］徐廷学.装备综合保障工程理论与方法［M］北京:兵器工业出版社，2009.143 －167.

XU Ting-xue.Integrated equipment support engineering theory and methods［M］.Beijing:National Defense Industry Press，2009.143 －167.

［3］王国胤，于洪，杨大春.基于条件信息熵的决策表约简［J］.计算机学报，2002，25(7):759 －766.

WANG Guo-yin，YU Hong，YANG Da-chun.Decision table reduction based on conditional information entropy［J］.Chinese Journal of Computers，2002，25(7):759 －766.

［4］苗夺谦，李道国.粗糙集理论、算法与应用［M］.北京:清华大学出版社，2008.21 －23，186 －190.

MIAO Duo-qian，LI Dao-guo.Rough sets theory algorithms and applications［M］.Beijing:Tsinghua University Press，2008.21 －23，186 －190.

［5］PAWLAK Z.Rough sets［J］.International Journal of Information and Computer Science，1982，11(5):341 －356.

［6］满江虹.基于粗糙集的分类知识发现方法及其应用研究［D］.南京:东南大学，2005.

MAN Jian-hong.Classification knowledge discovery methods and application based on rough sets theory［D］.Nanjing:Southeast University，2005.

［7］岳晓冬.基于粗糙集理论的连续值属性离散化方法研究［D］.太原:山西大学，2006.

YUE Xiao-dong.Research on discretization of continuous features based on rough sets theory［D］.Taiyuan:Shanxi University，2006.

［8］某型电台测试维修手册［M］.信息产业部电子第十研究所，2001.

Handbook of Some Radio testing and logistics support［M］.The 10thResearch Center of Ministry of Information，2001.

Application analysis of the equipment fault diagnosis based on rough set theory

ZHANG Guang-yi1，SU Yan-qin1，XU Ai-qiang2
(1.Graduate Student's Brigade，Naval Aeronautical and Astronautical University，Yantai 264001，China;2.Department of Scientific Research，Naval Aeronautical and Astronautical University，Yantai 264001，China)

Nowadays，the ability of the equipment fault diagnosis is very weak，so some kinds of fault diagnosis methods are compared and chosen rough set theory to be the suitable method for equipment fault diagnosis.Then the tested data of equipment status can be analyzed and be reduced the redundant information by the reduction algorithm of rough set theory，and the diagnosis rules can be got from the incorrect and incomplete testing data in decision table form.Then，the rough set theory is applied to some.

fault diagnosis;rough sets theory;radio equipment

TP181，V24

A

1672－7649(2012)01－0103－04

10.3404/j.issn.1672－7649.2012.01.025

2011－04－14;

2011－05－17

国家自然科学基金资助项目(60802088)

张光轶(1981－)，男，博士研究生，主要研究方向为装备故障诊断及预测、健康状态管理等。