居民消费价格指数的非参数自回归模型①

代洪伟， 凌能祥

(合肥工业大学数学系，合肥安徽230009)

居民消费价格指数是世界各国普遍编制的一种指数，它可以用于分析市场价格的基本动态，是政府制定物价政策和工资政策的重要依据．为准确把握居民消费价格指数的变动趋势，文献[1]利用ARIMA模型，对居民消费价格指数进行了预测分析，结果显示此模型用于预测居民消费价格指数比较好．但该模型的设定误差比较大，会影响预测结果，所以本文采用非参数自回归模型对居民消费价格指数进行模拟分析和预测，结果表明基于非参数自回归模型的居民消费价格指数预测可以获得令人满意的结果．

考虑如下的非参数自回归模型(NAR(p)模型):)

解释性变量Xt∈Rp是由响应变量(被解释性变量)Yt∈R的一些滞后项组成的(p为正整数);随机误差序列{εt}独立且同分布，E(εt)=0，E(ε2t)=σ2＞0，并且 εt与Xs(s≤t)相互独立;函数m(·)称为自回归函数(或条件均值函数)．

1 NAR预测模型

1．1 阶数p的确定

在应用NAR模型(1)对某个样本数据进行模拟和预测时，首先要确定模型的阶数p的值，本文利用Cross－Validation方法[5]确定模型的滞后阶数p．

Cross－Validation方法:对模型(1)的一段样本Y1，Y2，…，Yn，令Xt(k)=(Yt－1，Yt－2，…，Yt－k)，定义cv(k)，其中－t(·)是删去第t个数据后，对自回归函数m(·)的核估计，其阶数p可以用尝试阶数k替代，它的估计为

其中W(·)是适当选取的非负权函数，K(·)为核函数，给定NAR模型(1)的阶数的上界L，在{1，2，…，L}上极小化cv(k)，则阶数p的估计满足cv()=min1≤k≤Lcv(k)．

1．2 自回归函数的估计

自回归函数m(·)的常用估计方法是局部线性估计[6]和核估计法．虽然这两种方法有很多优点，但是二者均是局部光滑方法，在每一点处拟合自回归函数需求值时都需重新进行计算，计算量很大．而小波估计方法[9]、正交序列估计方法和样条估计等方法都属于全局光滑方法，能有效的克服这种弊端，计算效率较高．因此本文采用了全局光滑方法中的正交序列方法和样条方法对自回归函数进行拟合、估计．

1．2．1 正交序列估计

设自回归函数m(x)∈c[a，b]，假设构成[a，b]上的一组正交基，即=δij，当i=j时，δij=ci;当i≠j时，δij=0．则m(x)有正交序列展开m(x)=)．可将非参数自回归模型Yt=m(Xt)+εt近似为:

Yi对该模型进行最小二乘估计，得到^θ=(ZTZ)－1ZTY，其中，Z=(Z1，…，Zm)，Zi=(φi(X1)，…，φi(Xn))T．于是，m(x)有正交序列估计:^mn(x)=z(x)T^θ，其中z(x)=(φ1(x)，…，φm(x))T．

本文采用Legendre多项式正交基，在区间[－1，1]上，Legendre多项式的正交基为:

其他高阶Legendre多项式可由下式递推地推出:

(m+1)pm+1(x)=(2m+1)xpm(x)－mpm－1(x)，Legendre 多项式正交基满足，当i=j时，δij=1;当i≠j时，δij=0．

若解释变量X在区间[a，b]上取值，则必须作变量替换，变量Z的取值区间为[－1，1]．

1．2．2 多项式样条估计

样条估计基本思想:设Xt∈D=[a，b]，将区间[a，b]予以分割，结点序列为a=t0＜t1＜…＜tm＜tm+1=b．具有该结点序列的三次多项式样条空间S3，m的基函数Bs(·)可取为 1，x，x2，x3，(x－，其中(x－ti)+=max{0，x－ti}(i=1，2，…，m)．所以三次样条函数可表示为:，只要最小化就

可以得到θi的估计i(i=1，…，K)．则自回归函数m(x)的多项式样条估计为

多项式样条估计在实际应用中必须解决结点的选择问题．可按照如下方法选择结点:先取正整数k，令m=[n/k]，取ti=X(ki)(i=1，…m);对于第i(1≤i≤m)个结点，检验H0:θi=0，我们根据t统计量的值删除那些接受假设的结点;然后调整k的值直到获得比较理想的估计效果．

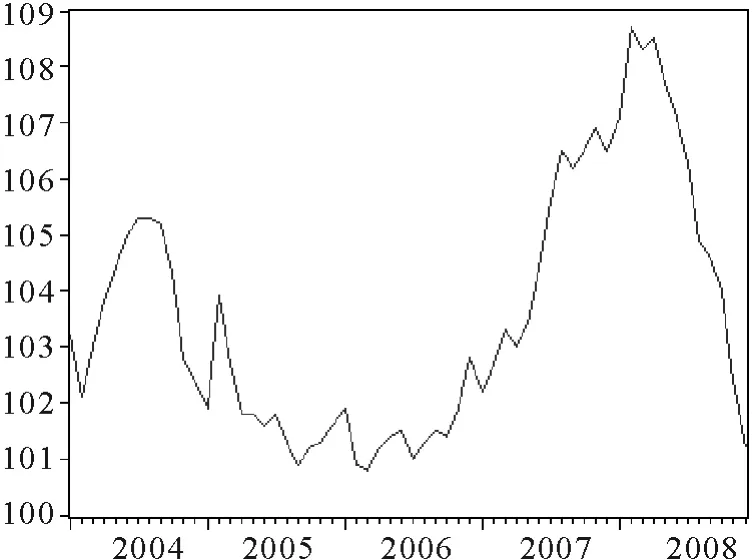
图1 我国2004．1 ～ 2008．12 CPI

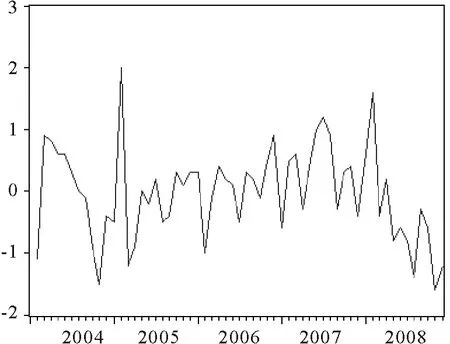
图2 我国CPI(一阶差分后)

1．3 非参数自回归模型的预测

本文使用循环预测法[7]对NAR模型进行预测，其基本方法如下:对NAR模型Yt=m(Xt)+εt，当k=1时(即对Yn+1预测时)，通过非参数方法对E(Yn+1|Yn=X)进行估计，算出一步预测值^Yn(1);当预测Yn+2时，可以把上面得到的^Yn(1)添加到(Y1，Y2，…，Yn)中构成新的样本(Y1，Y2，…，Yn，^Yn(1))，再采用上面一样的估计方法可以算出二步预测值^Yn(2)，像这样循环下去，直到我们得到k步预测值，因为在第k步预测时使用了Yn+1，Yn+2，…，Yn+k－1所包含的信息，所以，循环预测法比直接预测法的预测误差小．

2 我国居民消费价格指数的NAR预测模型

2．1 样本数据的选择与处理

本文的研究样本是我国2004年1月～2008年12月的居民消费价格指数的历史数据，首先对其建立NAR预测模型，然后用两种方法进行拟合，最后对2009年1月～2009年4月的居民消费价格指数进行预测．(数据来源于中国国家统计局网站)．

图1是我国2004年1月～2008年12月的居民消费价格指数的折线图，从图中数据可以看出:CPI序列是非平稳的时间序列，而我们只能对平稳的时间序列建立NAR模型．因此，若要对CPI序列建立NAR模型，首先要对其平稳化处理，在这儿我们采用一阶差分法．从图2可以知道一阶差分后CPI序列平稳．

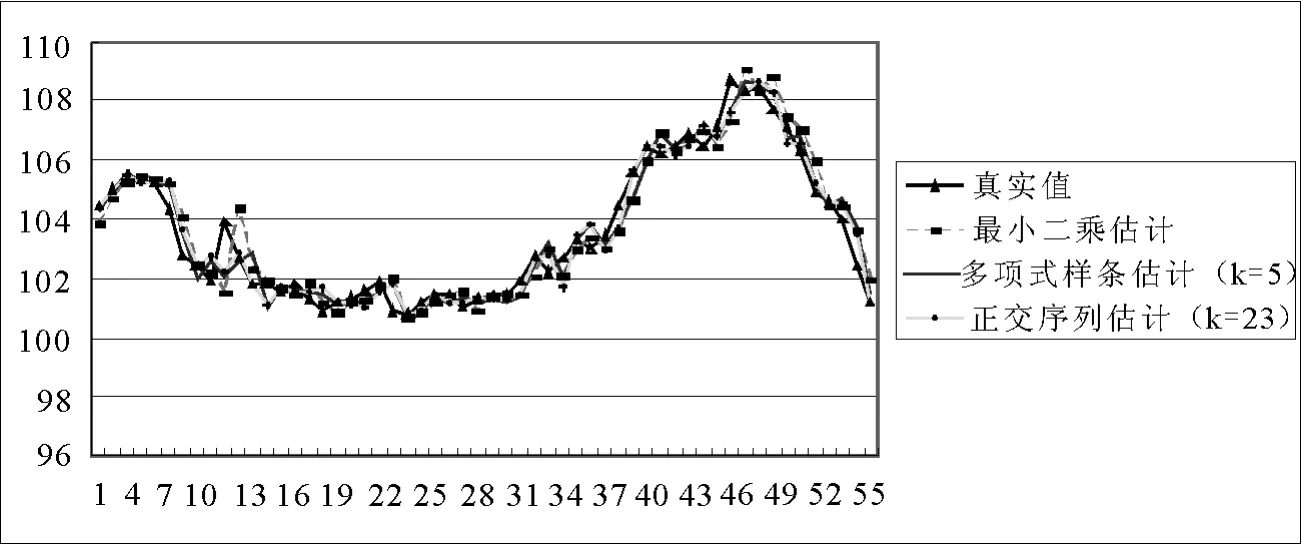
图3 CPI拟合曲线

2．2 ARMA模型的建立

首先对CPI差分序列{ΔYt}建立一个参数模型ARMA模型，通过比较差分序列的AIC值和偏自相关分析，得到最佳模型为AR(3)(其中AIC=2．19)． 通 过 计 算 得，其中模型的参数是通过最小二乘法估计得到的，括号中的数为T检验值．

2．3 NAR预测模型

对我国居民消费价格指数差分序列{ΔYt}建立 NAR 模型 ΔYt=m(ΔYt－1，ΔYt－2，…，ΔYt－p)+εt，其中随机误差序列{εt}独立且同分布，E(εt)=0，=σ2，εt与 ΔYt－1，ΔYt－2，…，ΔYt－p相互独立．

利用上述的Cross－Validation方法确定滞后阶p，当k=1时，cv(k)的值最小，因此NAR模型为ΔYt=m(ΔYt－1)+εt．

对我国2004—2008年的CPI差分序列{ΔYt}，建立 NAR 模型 ΔYt=m(ΔYt－1)+εt，并对该模型分别进行正交序列估计和样条估计．下图3给出了通过两种估计方法得到的我国CPI的拟合曲线与CPI原曲线，为了和参数模型进行比较，在图中也给出了用AR(3)模型拟合得到的曲线．

从图3中可以看出，三种估计方法都大致拟合出了我国CPI的具体走势，为了量化估计效果的比较，本文将三种估计方法的平均绝对误差与均方误差列于表1中，易见正交序列估计方法优于其他两种方法．

表1 平均绝对误差和均方误差的比较

由于我们建模的一个目的是为了预测，所以为了找出适合这类数据的理想模型和估计方法，我们用上面各种方法对样本进行预测，结果如表2．

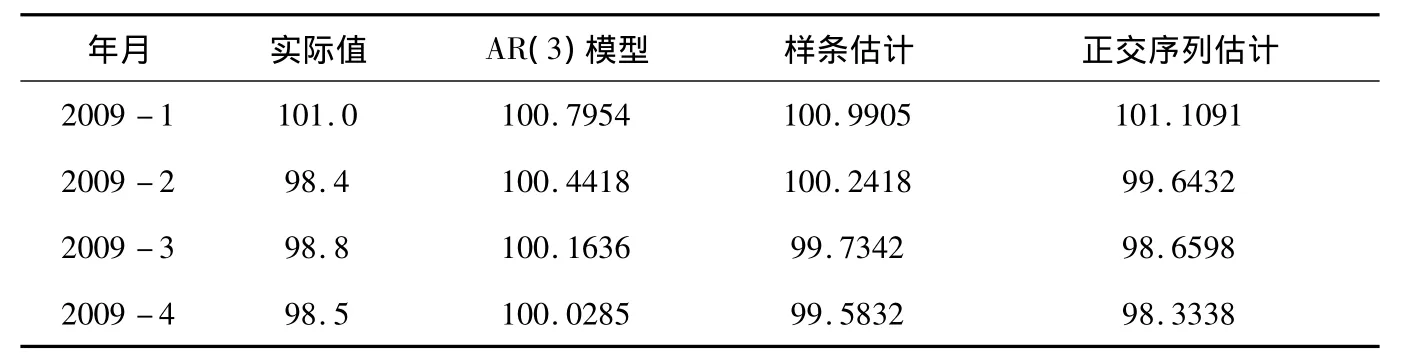
表2 预测结果

从两表的结果可以看出，在这3种估计方法中，正交序列估计方法的拟合效果及预测效果明显优于其他估计方法，最小二乘估计方法的模拟和预测效果是最差的．

表3是我们利用非参数自回归模型和文献[1]利用ARIMA模型对我国2004～2008 CPI进行模拟和预测的部分结果的比较．从表中可以看出非参数自回归模型要比ARIMA模型的模拟和预测结果理想．

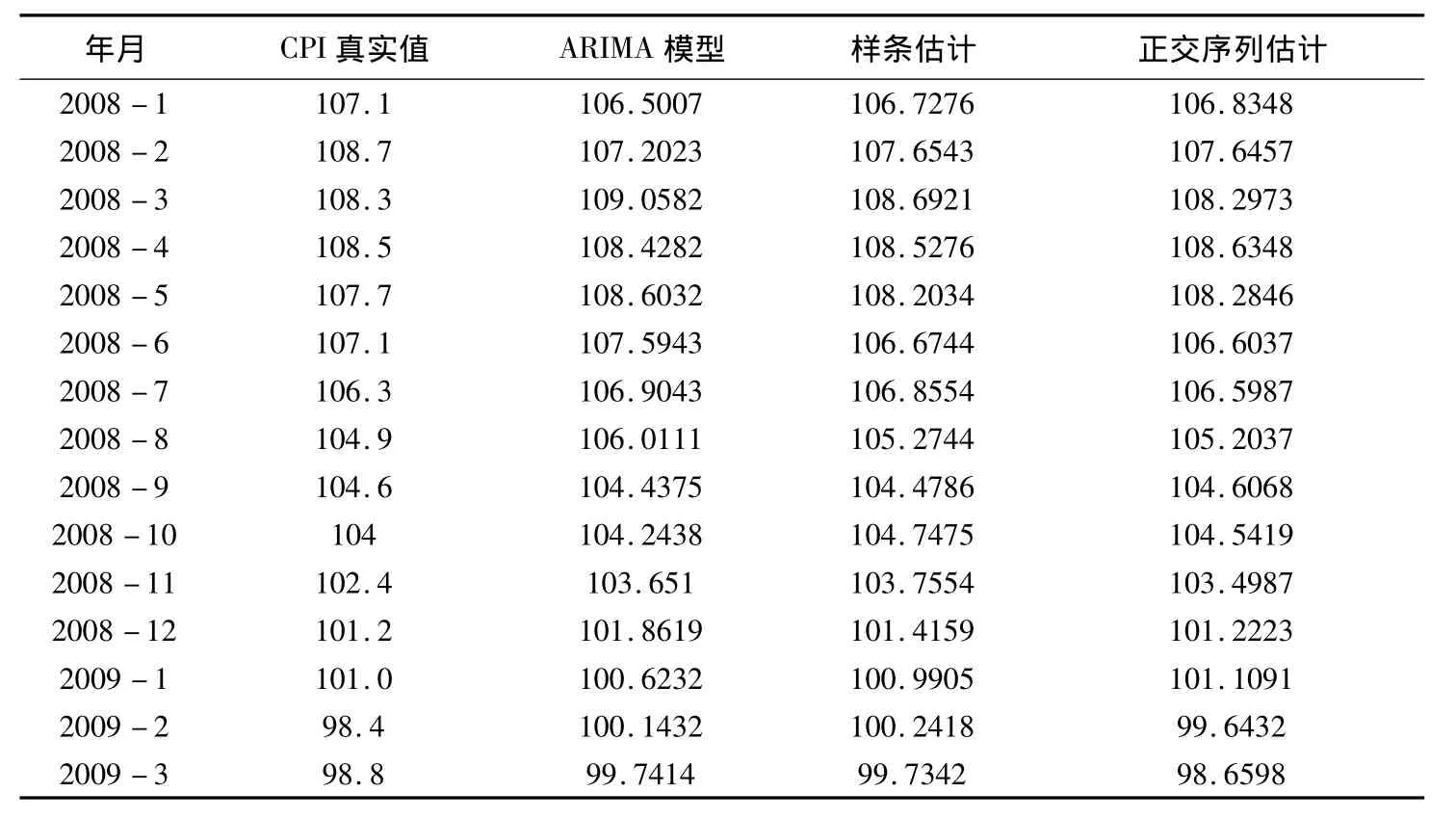
表3 模拟和预测结果的比较

3 结语

为了克服经典参数模型的缺点，本文利用2004～2008我国居民消费价格指数月度数据建立非参数自回归模型，并利用线性最小二乘估计、样条估计和正交序列估计进行拟合和预测，得到的结果表明:在这三种方法中，正交序列估计方法优于其他两种方法．

[1] 刘春燕，姚杰．时间序列分析在居民消费价格指数预测中的应用[J]．现代商贸工业，2010，(16)．

[2] 易丹辉．数据分析与Eviews应用[M]．北京:中国统计出版社，2002:106－132．

[3] 顾海燕．时间序列分析在人口预测问题中的应用[J]．黑龙江工程学院学报，2007，(9)．

[4] 叶阿忠．非参数计量经济学[M]．天津:南开大学出版社，2003．

[5] Wolfgang Hardle，Chen Rong．Nonparametric Time Analysis，a Selective Review with Examples[J]．Journal of Nonparametric Statistics，1995，27(5):157 －184．

[6] Masry E，Fan J．Local Polynomial Estimation of Regression Functions for Mixing Processes[J]．Scand J Statist，1997，24(2):165－179．

[7] Juan M Vilai－ Femandez．Nonparametric Forecasting in Time Series:A Comparative Study[J]．Communications in Statistics Simulation and Computation，2007，36(2):311 －334．

[8] 熊建平，吴建华，万国金．AR模型在人口增长预测中的应用[J]．计算机与现代化，2005，(10):11－12．

[9] 邹庆云，王国秋，王真伟．由最优双正交小波变换矩阵决定的小波基[J]．江西师范大学学报(自然科学版)，2009，33(1):69－73．