一类具有无穷时滞中立型泛函微分方程反周期解的存在性①

张洪彦， 王 奇， 丁敏敏， 王志杰

(安徽大学数学科学学院，安徽合肥230039)

0 引言

中立型泛函微分方程有着广泛的应用背景，人们对其周期解和概周期已有了深入的研究，例如文献[1－4]，在文献[4]中作者利用指数二分法和不动点定理给出了一类高维滞后型泛函微分方程

x(t)=A(t，x(t))x(t)+f(t，xt)

周期解的存在性，同时在文献[3]中作者利用指数二分法讨论了方程+G(t，x(t)，x(t－g(t)))的概周期解的存在性．

随着生产和社会的发展，反周期现象逐渐引起人们的关注，反周期在生物学，医学和各种物理工程现象中得到广泛的应用，因此许多学者对反周期解的存在性给予了大量研究，并得到一些结果，参见文献［5－9］．然而对中立型泛函微分方程反周期解问题的讨论甚少，本文讨论下面一类具有无穷时滞中立型泛函微分方程反周期解的存在性．其中x∈n，t∈．定义是n×n周期连续函数矩阵，函数G和Q是从n×n到n的反周期连续函数矩阵，且

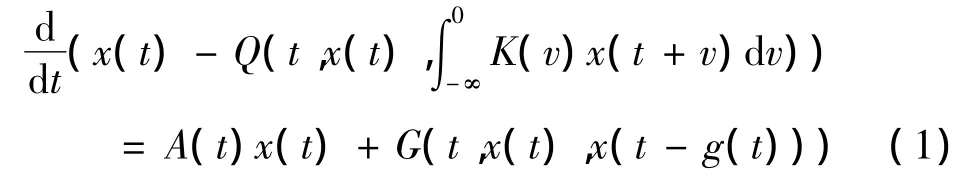
A(t+T)=A(t)，

G(t+T，－u，－v)=－G(t，u，v)，

g(t+T)=g(t)，

Q(t+T，－x，－y)=－Q(t，x，y)，

u，v，x，y∈n．本文利用指数二分法和压缩定理，证明了本方程反周期解的存在性．

2 准备知识

定义1 若u(t+T)=－u(t)，称连续函数u(t): → 是T反周期的．

显然当u(t+T)=－u(t)时，则u(t+2T)=u(t)．

定义范数

记PTA(，X)={u(t)|u为 → 的连续函数，u(t+T)=－u(t)}

则(PTA(，X)，‖·‖)为一Banach空间．

首先考虑线性系统

和

其中A(t)=(αij(t))n×n是 上的n维连续函数矩阵，f(t)是 上的n维连续向量函且A(t+T)=A(t)，f(t+T)=－f(t)．

对于A(t)=(αij(t))n×n，我们假设下面两个条件[7]:

(H1) 假设存在正可微函数d1(t)，d2(t)，

…，dn(t)(C1≤di≤C2，C1，C2为正的常数)以及连续的T周期函数α(t)，使得:

≤ α(t)dj(t)，j=1，2，…，n

引理1[10]设X(t)是系统(2)的一个基解矩阵，如果存在一个映射P和正常数α，β使得:则称系统(2)具有指数二分性．

引理2[4]对于方程(2)，A(t)若满足(H1)则

‖X(t)X－1(s)‖

若A(t)满足(H2)，则‖X(t)X－1(s)

其中X(t)为方程(2)的基解矩阵，满足X(0)=I

引理3[4](1)若A(t)满足条件(H1)，

且k1=，则方程(3)存在

唯一的T周期解:

本文研究数据显示，观察组颅内动脉瘤患者诊断符合率96.00%高于对照组，差异有统计学意义（P＜0.05）。观察组颅内动脉瘤患者误诊率和漏诊率均低于对照组，差异有统计学意义，P＜0.05。

(2)若A(t)满足条件(H2)，且k2=exp(－，则方程(3)存在唯一的T周期解:

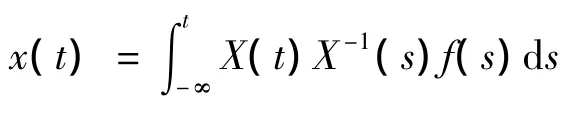
引理4 (1)若A(t)满足条件(H1)，且k1=exp(∫T0α(λ)dλ)＜1，则方程(3)存在唯一反周期解:

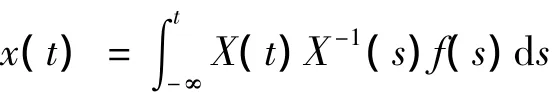
(2)若A(t)满足条件(H2)，且k2=exp(－，则方程(3)存在唯一反周期解:

证明 (1)由引理3知，方程有唯一有界解:

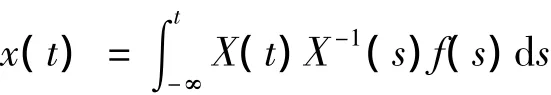
下面只需证明该有界解是反周期的即可．

又因X(t)是方程(2)的基解矩阵，则存在可逆矩阵B，使X(t+T)=X(t)B有

所以

即X(t)是反周期的，且是有界的．

(2)类似可证．

3 主要结论及证明

定理1 假设方程(1)满足条件(H1)且满足下列条件

(H3)

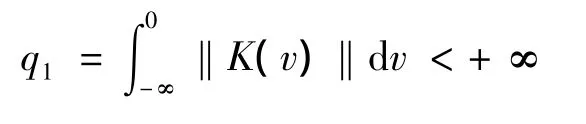
(H4)存在常数L1，L2，L3，L4，L5和u1，v1，u2，v2，x1，y1，x2，y2∈PTA( ，X)使得下列式子成立

其中k1=和＜ 1．则方程(1)存在反周期解．

证明

对任意的u(t)∈PTA(，X)，首先考虑方程

设

则有

其中

由前面介绍知h(t+T)=－h(t)，即h(t)是T－反周期的．

根据假设条件和引理4知，方程(5)存在唯一的反周期解:

从而方程(4)有唯一的反周期解:

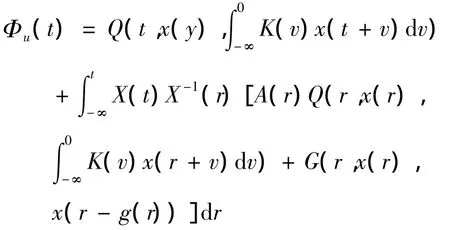
作映射Γ:PTA(，X)→PTA(，X)如下:

Γu(t)=Φu(t)，(∀u∈PTA(，X))下面证明Γ是压缩的．

事实上，对 ∀u1，u2∈PTA( ，X)，有

由条件(H5)知

因此Φ在PTA(，X)是压缩的，由压缩不动点定理知，Φ在PTA(，X)中存在不动点，此不动点即为方程(1)的反周期解．证毕．

定理2 假设方程(1)满足条件(H2)，(H3)，(H4)和(H6)

其中

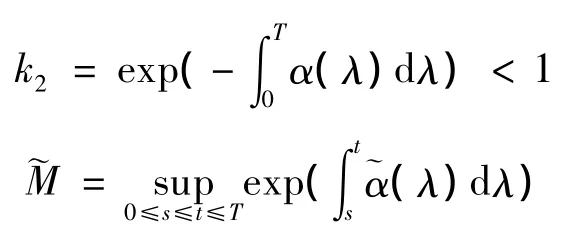
则方程(1)存在反周期解．

证明 方法类似定理1．证毕．

4 例 子

考虑系统:

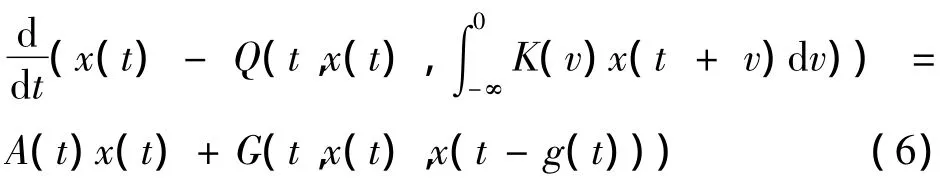
其中

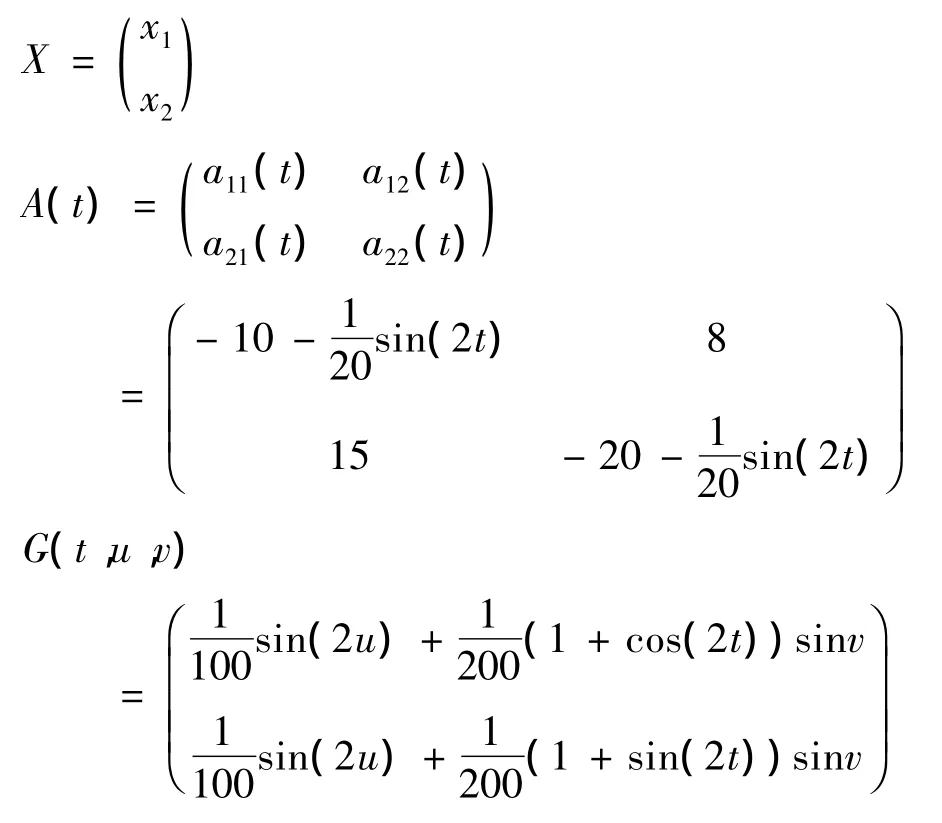
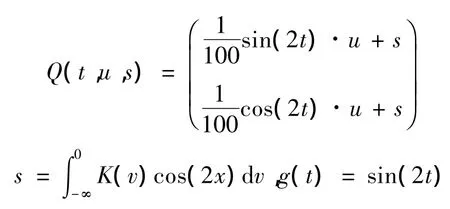
取d1(t)=2，d2(t)=1，

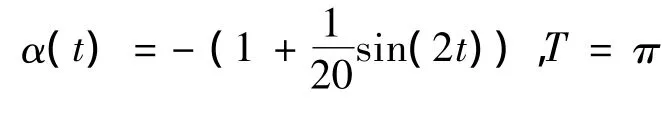
且有

另外经过简单的计算可以得到:

则有

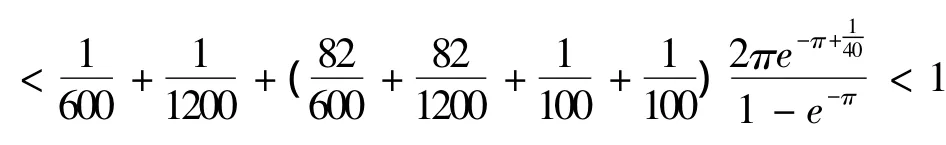
即方程(6)满足条件(H1)，(H3)，(H4)，(H5)，由定理1可知方程(6)存在一个π反周期解．证毕．

[1] 彭世国朱思铭．具有无穷时滞泛函微分方程的周期解[J]．数学年刊，2002，23A:371 －380．

[2] 石磊．具有无穷时滞中立型泛函微分方程解的有界性及周期解[J]．科学通报，1990，35:409 －411．

[3] Xiaoxing Chen，Faxing Lin．Almost Periodic Solutions of Neutral Functional Differential Equations[J]．Nonlinear Anal．，2010，11:1182－1189．

[4] 周宗福．一类高维滞后型泛函微分方程的周期解[J]．数学杂志，2002，22(4):423 －430．

[5] Yan Wang．Antiperiodic Solutions for Dissipative Evolution Equations[J]．Mathematical and Computer Modelling．2010，51:715－721．

[6] Aizicovici S，McKibben M，Reich S．Anti－periodic Solutions to Nonmonotone Evolution Equations with Discontinuous Nonlinearities[J]．Nonlinear Anal．2001，43:233 － 51．

[7] Aizicovici S，Pavel N．Anti－ periodic Solutions to a Class of Nonlinear Differential Equations in Hilbert Space[J]．J Funct Anal．1991，99:387 －408．

[8] Aizicovici S，Reich S．Anti－periodic Solutions to a Class of Non － monotone Evolution Equations[J]．Discrete Contin Dyn Syst．1999，5:35 －42．

[9] Chen Y．Anti－periodic Solutions for Semilinear Evolution Equations[J]．J Math Anal．Appl，2006，315:337 － 348．

[10] 林发兴．线性系统指数型二分性[M]．合肥:安徽大学出版社，1999．