基于ELMAN神经网络的短期风速预测

孙 斌，姚海涛，齐城龙

(1.东北电力大学能源与动力工程学院，吉林吉林132012;2.内蒙古大唐国际红牧风电场，内蒙古乌兰察布012000)

能源与环境是当今人类生存和发展所急需解决的问题。常规能源以煤、石油、天然气为主，它不仅资源有限，而且还造成了严重的大气污染。因此，对可再生能源的利用，尤其是对风能的开发利用，已受到各个国家的高度重视。随着风能利用的加速发展，越来越多的大型风电场将纳入统调电网，风电在电网中的比重越来越大，但是由于系统的最大负荷受限于风电场穿透功率极限，所以当负荷超过一定值的后，就会严重影响电能的质量以及电网运行的安全稳定。而对风速的准确预测可以减少风电场的旋转设备和运行成本，提高风电穿透功率极限，可以帮助调度部门及时调整计划，从而减轻风能对电网的冲击［1-2］。

目前，风速预测的方法有卡尔曼滤波法［3］、时间序列法［4］、空间相关性法［5］等。用神经网络处理时间序列是一个热点问题。Elman网络是一种典型的动态神经网络，它在前馈人工神经网络基本结构的基础上，通过存储内部状态使其具有映射动态特征的功能，从而使系统具有适应时变特性的能力。在Elman网络中的前馈权值通常采用BP算法调整，而反馈权值设定为常数。因此，为了保证收敛性，在网络的训练过程中需要反复调整前馈的权值，寻找其最优解。

同时，用混沌动力学处理时间序列是一个热点问题，在很多领域开始得到应用，如信号检测［6］、两相流［7］、环境［8］、交通［9］等领域。本文尝试用运算速度更快，运算精度更高的Elman神经网络模型同混沌理论相结合进行预测，同时与BP神经网络的预测结果做了比较，预测结果表明Elman神经网络模型在短期风速时间序列的预测中取得了较好的预测结果。

1 Elman神经网络原理

Elman型回归神经元网络一般分为4层:输入层，中间层(隐含层)，承接层和输出层，见图1。其输入层，隐含层和输出层的连接类似于前馈网络，输入层的单元仅起信号传输作用。隐含层单元的传递函数可采用线性或非线性函数。承接层又称上下文层或状态层，它用来记忆隐含单元前一时刻的输出值，可以认为是一个一步延时算子。其特点是隐含层的输出通过承接层的延时与存储，自联到隐含层的输入，这种自联方式使其对历史状态的数据具有敏感性，内部反馈网络的加入增加了网络本身处理动态信息的能力，从而达到了动态建模的目的［10-12］。理论证明，具有三层计算单元的神经网络可以实现任意复杂的映射。因此一般情况下，只采用含有一个隐层的网络。基于以上思想，本文亦采用只含有一个输入层，一个隐含层，一个承接层和一个输出层的Elman网络。

图1 Elman神经网络模型

Elman神经网络的非线性状态空间表达式为

式中:k为神经网络训练的次数;y为n维输出向量;x为隐层神经元输出向量;u为输入向量;xc为反馈状态向量;w3、w2、w1分别表示隐层到输出层、输入层到隐层、承接层到隐层的连接权值矩阵;g(·)为输出神经元的传递函数，是中间层输出的线性组合;f(·)为隐层神经元的传递函数。Elman神经网络采用BP算法进行权值修正，学习指标函数采用误差平方和函数［13-15］:

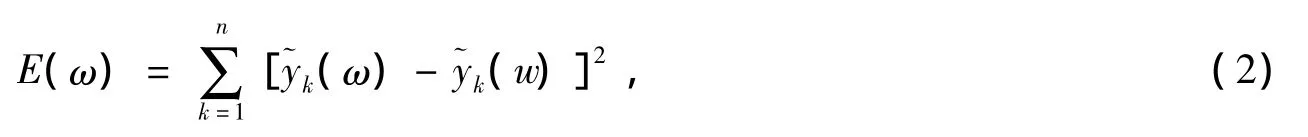
在Elman神经网络中，输入信号决定反馈系统的初始状态，系统经过一系列状态转移后，逐渐收敛于平衡状态，即网络的输出结果。可见，稳定性是Elman神经网络最重要的特点之一［13-15］。因此只要适当地设计其连接权和输入就可找到系统稳定点，且收敛速度较快。这是在模式识别中Elman神经网络优于BP网络之处。

2 相空间重构

提出相空间重构的最初目的在于把混沌吸引子在高维相空间中恢复过来。混沌吸引子作为混沌系统特征之一，它体现着混沌系统的规律性，也就是混沌系统最终会进入一个特定的轨迹之中，这种特定的轨迹也就是吸引子。一般情况下时间序列的相空间维数很高，但是维数我们往往不知道。因此为了把时间序列的信息充分显示出来，我们通常将其扩展到三维或是更高的空间去，这就是时间序列的相空间重构。

Taken定理［16-17］:若M是d维流形，φ:M→M，φ是一个光滑的微分同胚，y:M→R，y有二维连续导数，φ(φ，y):M → R2d-1。其中:φ(φ，y)= ［y(x)，y(φ(x))，…y(φ2d+1(x)］。

根据G-P算法:对于时间序列x(1)，x(2)，…x(t)，…x(N)，当嵌入维数为m和延迟时间为τ时，重构相空为

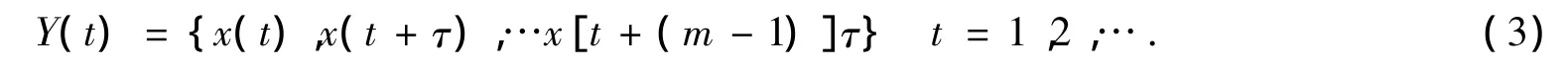
综上可知，在时间序列相空间重构中，延迟时间τ和嵌入维数m的选取具有重要意义。其确定方法有很多，本文运用自相关法和假近邻法分别求出风速时间序列的延迟时间和嵌入维数。

3 风速预测结果分析

本文以东北某风电场2010年12月份的实测风速时间数列作为实验样本，每小时作为一个采样点，选取其中连续的500 h的风速数据作为实验数据见图2。

其中前350个风速数据作为训练样本，后150个风速数据作为训练样本用于检验预测结果的真实性。对于数据在传输和记录过程中可能出现的错误，在预测之前对数据进行了预处理，然后再对风速时间序列进行相空间重构。

在进行相空间重构之前对实验数据进行归一化处理，以减小奇异样本而导致的训练时间的增加。然后求出嵌入维数和延迟时间分别对实验数据相空间重构以获得重构后的分析数据。

图2 原始风速时间序列

运用自相关法和假近邻法分别求出延迟时间和嵌入维数。嵌入维数的判定方法:随着嵌入增加虚假近邻数不断的减少，当虚假近邻数随嵌入维数的增加接近为0或不再变化的时候，相应的嵌入维数就是所求值。由图3可知最小嵌入维数m=4。图4描述了风速时间序列的自相关函数曲线图，当自相关曲线下降到初始值的1-1/e时，所对应的延迟时间即为相空间重构的最佳延迟时间。由此确定的最佳延迟时间τ=8。然后根据公式(3)对训练数据和预测数据分别进行相空间重构。

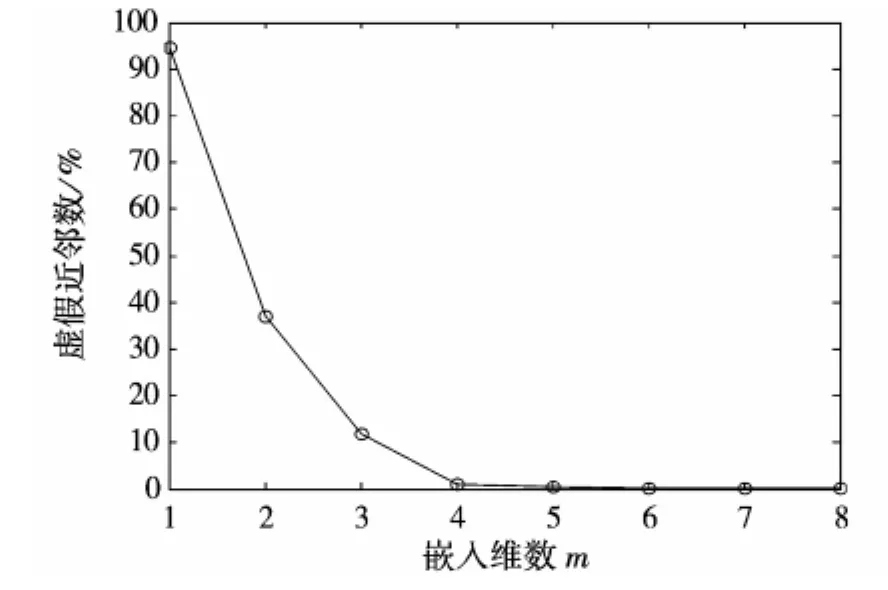
图3 风速时间序列的嵌入维数

图5为二维风速时间序列时间序列相图，可以从风速时间序列的相图可以看出其轨迹反复折叠和相互交叉形成在左下角形成了一个稠密带，所以判定风速时间序列吸引子的存在，从而推断出风速时间序列具有混沌性。

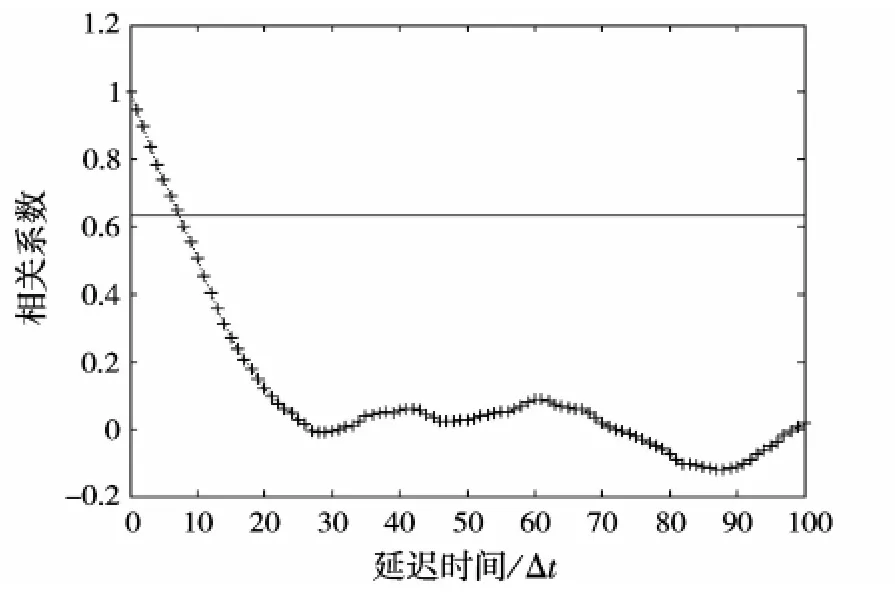
图4 风速时间序列的延迟时间

图5 风速时间序列相图

首先运用训练数据对Elman神经网络进行训练，然后用训练好的Elman神经网络模型对风速时间序列进行预测见图6(测试数据与预测数据均已归一化)，同时与BP神经网络预测进行了比较。BP神经网络预测结果见图7(测试数据与预测数据均已归一化)。Elman神经网络、BP神经网络对风速时间序列预测的均方根和预测所用时间见表1。Elman神经网络、BP神经网络对风速时间序列预测的预测时间分别是6 s、9 s。模拟结果表明，Elman神经网络模型同BP神经网络模型相比，有预测速度快，预测精度高的优点。

图6 Elman神经网络模型风速预测

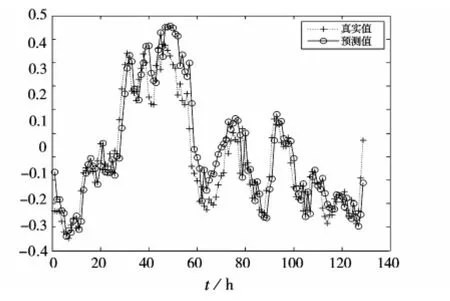
图7 BP神经网络模型风速预测

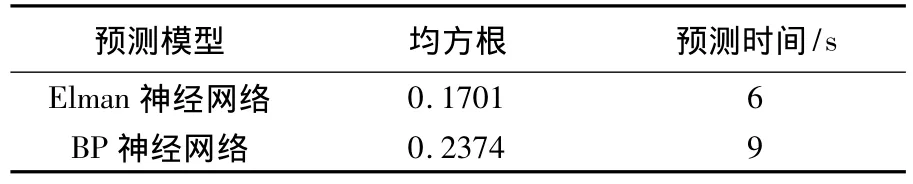
表1 归一化后的方均根比较

4 结 论

本文研究了风速时间序列的混沌特性，对风速时间序列进行了相空间重构，运用Elman神经网络模型对重构后的风速时间序列进行预测，将混沌理论引入风速预测中取得了很好的预测效果。与传统的BP神经网络相比，具有学习速度快、预测精度高等优点。因此，Elman神经网络模型在风速时间序列的预测上更加有效。

［1］袁铁江，晁勤，李义岩，等.基于风电极限穿透功率的经济调度优化模型研究［J］.电力系统保护与控制，2011，39(1):15-22.

［2］魏晓霞.我国风电发展存在的问题和应对措施［J］.电力技术经济，2009，21(6):23-26.

［3］Bossanyi E A.Short-term wind prediction using Kalman filters［J］.Wind Engineering，1985，9(1):1-8.

［4］Kamal L，Jafri Y Z.Time series models to simulate and forecast hourly averaged wind speed in Wuetta，Pakistan［J］.Solar Energy，1997，61(1):23-32.

［5］Alexiadis M C，Dokopoulos P S，Sahsamanoglou H S .Wind-Speed and Power Forecasting based on Spatial Correlation Models［C］.IEEE Transactions on Energy Conversion，1999，14(3):836-842.

［6］陈伟根，张嵩，杜林，等基于互相关与混沌检测相结合的光声信号检测方法［J］.电力自动化设备，2008，28(3):22-28.

［7］周云龙，李洪伟，宋均琪，等.垂直上升管中油-气-水三相流动态图像灰度波动信号的混沌特性分析［J］.石油学报(石油加工)，2009，25(4):600-606.

［8］Ajit Kumar Gautam，A.B.Chelani，V.K.Jain.A new scheme to predict chaotic time series of air pollutant concentrations using artificial neural network and nearest neighbor searching［J］.Atmospheric Environment，2008，13(11)，4409 – 4417.

［9］Xi-Yue，Li-Sheng Yin，et al.Pridiction for Chotic Time Series Based on Discrete Volterra Neural Network.［J］.Lect Notes Computer SC，2006，27(9):759-764.

［10］Cheng Y C，Qi W M，Cai W Y.Dynamic properties of Elman and modified Elman neural network［C］.2002 International Conference on Machine Learning and Cybernetics，2002(2):637-640.

［11］李锡杰，师硕，王旭.基于Elman神经网络的肌电信号分类［J］.人工智能，2006，22(8):305-306.

［12］Pham D T，Liu X.Training of Elman networks and dynamoic system modeling［J］.International Journal of Systems Science，1996，27(2):2212-2261.

［13］Li Xiang，Chen Guanrong，Chen Zengqian et al.Chaotifying linear Elman networks［J］.IEEE Transactions on Neural Networks 2002，13(5):1193-1199.

［14］Cheng Y L，Huang J C，YangW C.Modeling word perception using the Elman network［J］.Neurocomputing，2008，71(16/17/18):3150-3157.

［15］Gao X Z.Gao X M.Ovaska S J.Trajectory control based on a modified Elman neural network［C］.Orlando Florida，USA:IEEE International Conference on SMC，1997.1995，6(5):1212-1228.

［16］吕金虎，陆军安，陈士华.混沌时间序列分析及应用［M］.武汉:武汉大学出版社.2002.

［17］陈敏，李泽军，，黎昂.基于混沌理论的城市用电量预测研究［J］.电力系统保护与控制，2009，37(16):41-45.