柔性接头界面端角点应力奇异性①
安春利,任全彬,王铁军,赵桂平
(1.中国航天科技集团公司四院四十一所,西安 710025;2.西安交通大学,西安 710049)
柔性接头界面端角点应力奇异性①
安春利1,任全彬1,王铁军2,赵桂平2
(1.中国航天科技集团公司四院四十一所,西安 710025;2.西安交通大学,西安 710049)
基于界面理论,建立了柔性接头增强件、弹性件两种结合材料形成的界面端角点附近奇异应力场方程,依据界面连续条件和自由边界条件,得到了与奇异应力场关联的特征值λ的线性齐次方程组,通过该方程组的求解和公式推导,给出了柔性接头界面端角点附近含应力强度系数的奇异应力场和位移场;并根据特征值λ的取值范围,获得了应力奇异性消失的柔性接头弹性件、增强件材料匹配和几何形状角选择。选取柔性接头常见工况,分别进行了角点附近奇异应力场解析解计算和有限元计算,验证了解析解的正确性。
柔性接头;应力奇异性;界面端角点;特征值;应力强度系数
0 引言
柔性接头依靠粘接面传递载荷,粘接界面是高分子材料组成的界面相,该界面相将增强件和弹性件粘接在一起,由于弹性件、增强件为球形环状薄片,导致在每层粘接面处存在界面端角点。柔性接头漏气破坏模式出现的主要原因:一是由粘接面某处脱粘或弱粘引起脱粘面的扩展而形成的漏气通道;二是粘接面端部角点处存在应力奇异性。摆动中,角点部位率先形成脱粘源,随之脱粘部位不断扩大,形成贯穿性气体通道,最终导致结构漏气。漏气的第一个原因属于传统意义上的界面强度问题,第二个原因则是由于设计参数不合理,致使粘接面角点的应力奇异性造成局部应力趋于无穷大,属于界面力学范畴。工程研制中柔性接头的破坏源,往往发起于界面端角点,因而柔性接头粘接界面端角点,成为研究柔性接头问题的一个焦点。
本文针对柔性接头的第二个破坏原因,建立并求解了柔性接头界面端角点的奇异应力场,根据与奇异应力相关的特征值λ取值范围,研究了柔性接头弹性件、增强件常见材料组合情况下的应力奇异性消失的几何形状角选择。
1 结合材料定义及柔性接头界面应力奇异性
1.1 结合材料定义
物性不同的异类材料,利用粘接、绑定等结合方法连接在一起、作为整体结构使用,称为结合材料,由于是2种不同的材料结合在一起,材料参数共有4个弹性常数,即2个杨氏模量E或剪切模量,以及2个泊松比ν。对于诸多问题,这4个常数对结合材料应力应变的影响互相耦合,可用2个新的组合材料参数来描述,称为 Dundurs参数[1-2]。
Dundurs参数:

式中E为弹性模量;ν为泊松比;下标为材料代号。
柔性接头是由橡胶弹性件和金属或复合材料增强件粘接而成的构件,符合结合材料的定义,结合材料的理论同样适用于柔性接头。
1.2 柔性接头界面应力奇异性
柔性接头的轴对称界面角点和界面端模型见图1。图1中,z轴为柔性接头对称轴,通过几何形状角θ1、θ2和界面位置角θ0取值,可对柔性接头的轴对称界面端问题进行分析。
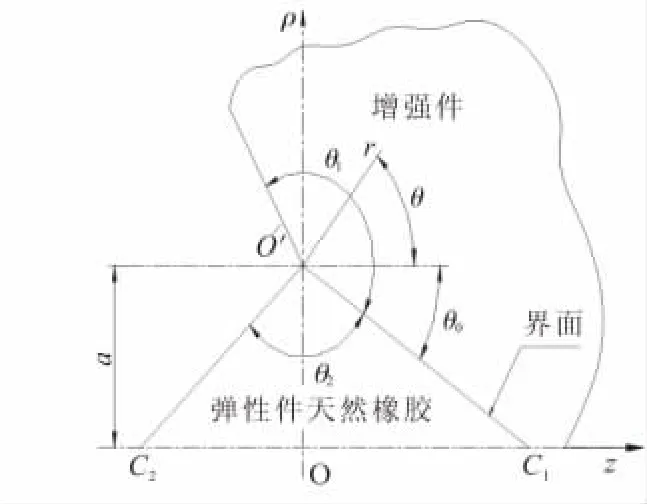
图1 柔性接头轴对称界面端模型Fig.1 Axisymmetric model of interface corner in flexible joint
图1 中(ρ、φ、z)为圆柱坐标系;ρ、z轴的取法见图1;φ为圆周方向的角坐标;应力奇异点为O'。
轴对称问题,应力和位移可用2个调和函数来表示[3-4]:
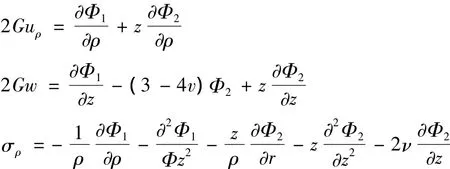
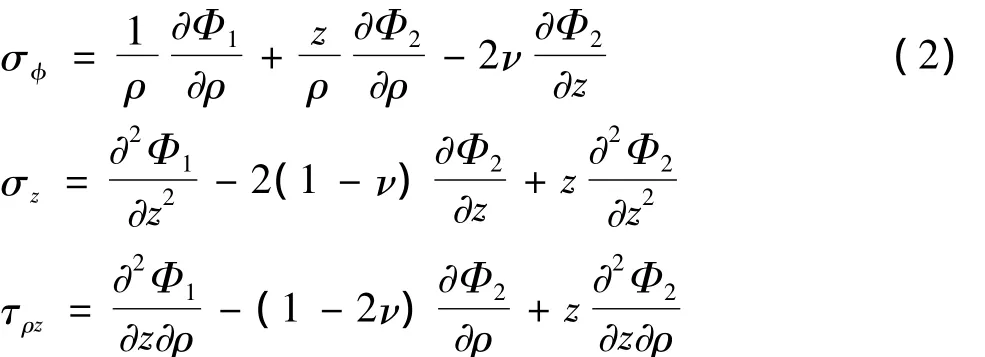
函数Φj为调和函数,满足:

图1中,界面连续条件和自由边界条件可表示为
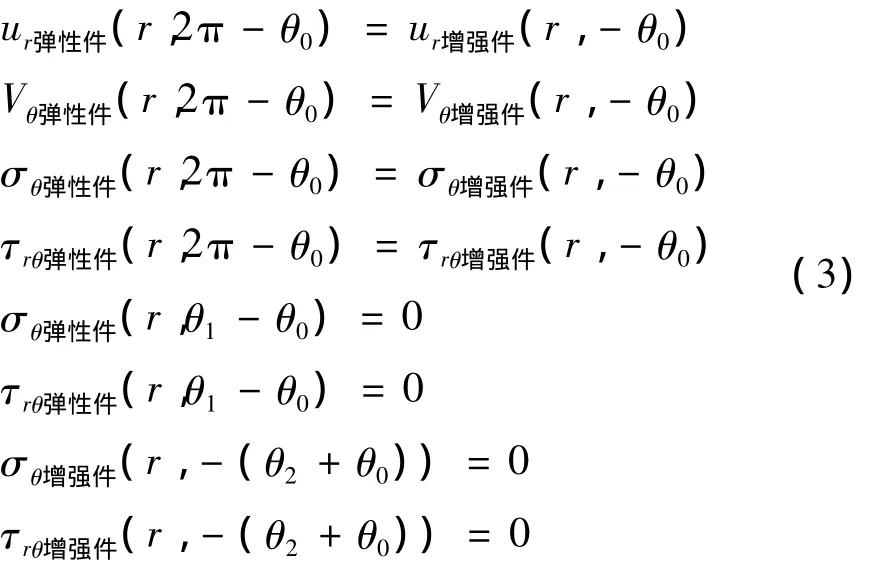
要确定应力和位移分量,必须确定2个调和函数具体的函数关系式,而2个调和函数可用含待定系数的级数型式给出,问题转化为求调和函数级数形式的待定系数,界面连续条件与自由边界条件与调和函数结合。经整理[5-7],得到关于待定系数的线性齐次方程组,根据其有非零解的条件,其系数矩阵的行列式等于零,得到含特征值λ的特征方程,求得了特征值,可进一步得到非零的系数解,从而完整的给出奇异应力场和位移场。
针对图1,特征方程为
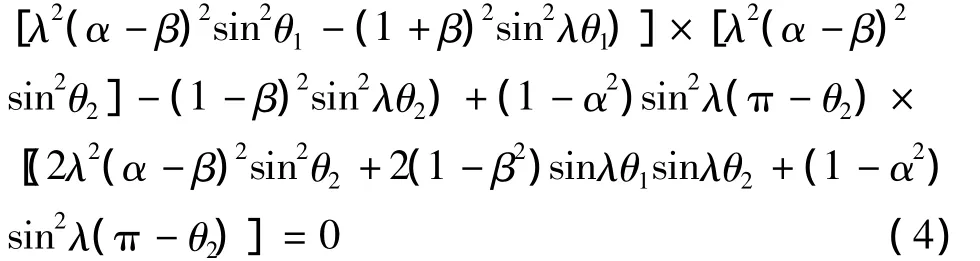
其中,α、β 为 Dundurs参数(k=3-4ν),即该特征方程式中的Dundurs参数与平面应变状态下的Dundurs参数相同。
当给定结合材料及其界面端形状后,λ为表征界面端应力场强度的应力奇异性指数,也为方程(4)的特征值,该方程因此被称为界面端的特征方程。考虑到即使存在非零的常应力场,在界面端附近起支配作用的仍是奇异项。只考虑0<Re(λ)<1的特征值。
界面端角点附近的应力场(当r→0)可近似表述为
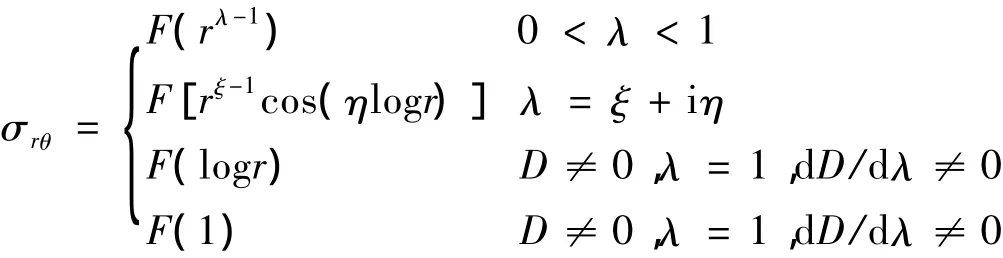
式中 ξ、η是特征值λ的实部、虚部;D是行列式。
2 柔接头界面端角点附近应力场求解
方程(4)的求解过程,国内外学者已做了大量工作,本文不再多述。如果特征方程有多个特征值,则依据叠加原理求解,以两个特征值λ1和λ2为例,界面端奇异点O附近在材料m(m=1,2)中的位移场和奇异应力场可分别表示为

式中K1与K2,fkm1(θ)与fkm2(θ),Fkm1(θ)与Fkm2(θ)分别为对应于特征值λ1与λ2的应力强度系数、位移函数和应力函数;fkm1(θ)、fkm2(θ)、Fkm1(θ)、Fkm2(θ)是随角度的变量,而K1、K2是定参数,需求解。
为确定结合材料界面端的应力强度系数K1、K2,需沿θ=θ0方向选择2种已知应力分量σ(1)与σ(2),则有
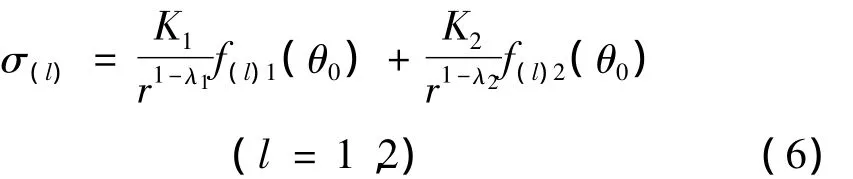
联立求解组成的方程,可得到K1、K2。
3 柔性接头界面端应力奇异性消除
一般情况下,方程(4)可能存在无穷多个根,界面端附近应力场的奇异性指数一般可由方程(4)所给出的根的最小实部Re(λ)表示,Re(λ)≤0时,界面端的位移趋于无穷大,没有物理意义Re(λ)≥0时,界面端所对应的应力趋于零,是一个高阶微量,λ=0时,对应的是一个刚体位移或常应力场。显然,如果方程(4)仅存在Re(λ)≥1的根,界面端附近奇异应力场将会消失,考察方程(4),当材料的(α、β)组合确定,通过Re(λ)≥0,并合理设定 λ 值,改变(θ1、θ2)值,就可找到应力奇异性消失的根和(θ1、θ2)组合。
4 算例
4.1 计算结果
某型号柔性接头增强件材料30CrMnSiA,弹性件材料天然橡胶,Dundurs参数计算值 α=0.999,β=0.01,4个界面端角点位置、位移编号见图2。
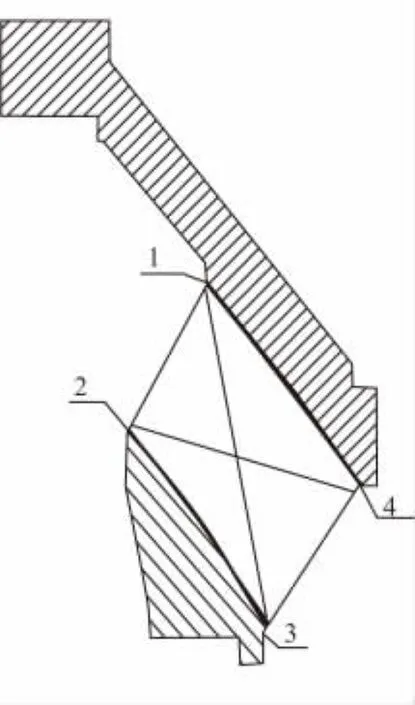
图2 柔性接头奇异点编号Fig.2 Singular point number of flexible joint
图2中,角点1计算的位移和应力如下:
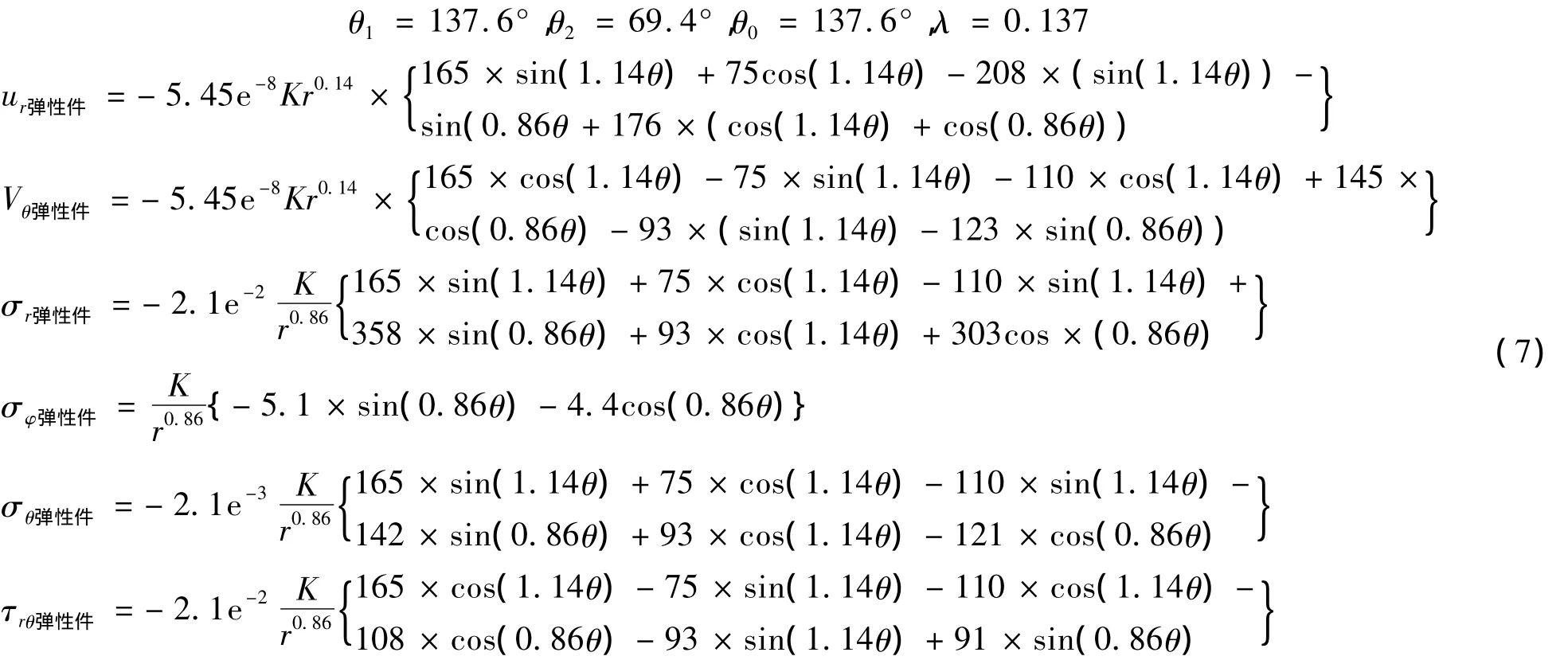
式中K是与工况相关的应力强度系数。
4.2 验证
4.2.1 界面端角点附近奇异应力场验证
某柔性接头承受1.6 MPa水压反向拉伸,界面承受拉剪应力,界面应力无法实测,本文采用具有强健计算功能和广泛模拟性能的ABAQUS有限元软件,计算出柔性接头粘接界面角点附近的应力。然后,以有限元法计算的应力值来验证本文给出的解析解计算结果的正确性,柔性接头反向水压拉伸工况有限元网格划分时,在考虑计算机能力的前提下,分别取单元长度与r=5×10-1mm比值为1、5、10进行了计算,并进行了比较,计算结果见图3、图4。
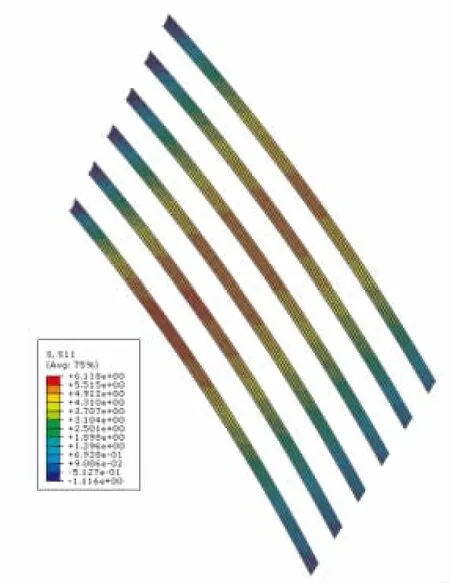
图3 弹性件轴向应力Fig.3 Axisymmetric stress of elastomer
针对奇异点1,选取r=5×10-1mm,以有限元计算的σr为基准,计算得到应力强度系数K=1.35×10-3,依次应用解析解推得r=5×10-1mm其他位置的σr值,并与有限元结果比较,见表1。

图4 增强件Mises应力Fig.4 Mises stress of reinforcement
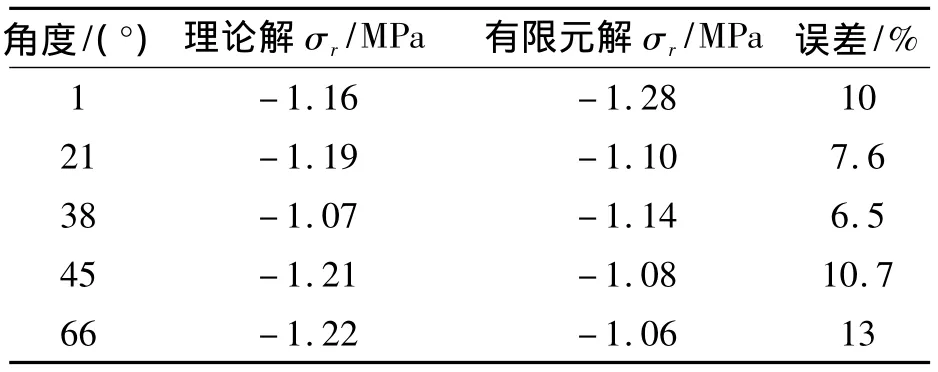
表1 某柔性接头奇异点1,r=5×10-1mm处解析解与有限元解比较Table 1 Theoretical and FEM calculation comparison in singular point 1,r=5 ×10-1mm
反向水压工况下径向应力理论解与有限元计算结果比较表明,最大误差为13%,且应力趋势一致,证明柔性接头粘接界面角点的应力理论解基本正确,可用来计算柔性接头粘接界面角点附近应力和指导柔性接头参数设计。
4.2.2 界面端角点应力奇异性消失几何形状角组合研究
根据某型号柔性接头的结构尺寸,依次将增强件材料换为30CrMnSiA、钛合金、铝合金、炭布,弹性件材料模量在 0.1、1.0、2.0 MPa 之间选择,分析了平面应变和平面应力状态下的应力奇异性消失组合,结果见图5、图6及表2。

图5 平面应变组合角曲线Fig.5 Change of angle in planar strain

图6 平面应力组合角曲线Fig.5 Change of angle in planar stress
结果表明,采用曲线下方的任意角度组合,都可消除柔性接头界面端角点的应力奇异性,但采用不同的角度组合,对界面角点附近的应力分布规律的影响是不同的。同时还应注意,对于柔性接头,弹性件材料的配方基体是橡胶,其弹性模量变化不大;而对于增强件,材料为炭布/酚醛时,其应力奇异性消除的角度组合范围较宽。因此,在能满足增强件强度要求的前提下,应尽量选用非金属复合材料,以减少粘接界面角点的应力奇异性。
对于钢和弹性件粘接,应力奇异性消失的组合角度范围相对较窄,但钢和弹性件的粘接,却是一种常用结构方式。图6显示θ1在20°范围内时,θ2可取137°之内的值,当 θ2在 55°以下时,θ1取值方位较广,θ1、θ2在这些范围内取值,界面端角点均无应力奇异性产生。
5 结论
建立了适用于固体火箭发动机喷管柔性接头界面端角点附近奇异应力和位移的理论计算公式,理论公式结果表明,应力和位移奇异性与弹性件、增强件材料组合和几何形状有关,柔性接头的结构失效,界面端角点的应力奇异性是一个重要的诱导因素;通过不同材料匹配和几何形状角选择,可有效消除角点应力和位移的奇异性;同时,界面角点附近的奇异应力场与柔性接头所受载荷紧密相关。柔性接头反向水压工况的有限元仿真结果,验证了理论公式解的正确性。
[1]许金泉.界面力学[M].北京:科学出版社,2006.
[2]Bogy D B.Edge-bonded dissimilar orthogonal elastic wedges under normal and shea loading[J].Journal of Applied Mechanics,1968,35:460-466.
[3]刘一华,许金泉,丁皓江.轴对称界面端的应力奇异性[J].浙江大学学报.1998,32:307-314.
[4]Liu Y H,Xu J Q,Ding H J.Order of singularity and singular stress field about an axisymmetric interface corner in three dimensional isotropic elasticity[J].Int.J.Solids Struct.,1999,36:4425-4445.
[5]Dundurs J.Discussion of edge boned dissimilliar orthogonal elastic wedges under normal and shear loading[J].Journal of Applied Mechanics,1969,36:650-652.
[6]Dundurs J.Effect of elastic constants on stress in a composite under plane deformations[J].Journal of Composite Materials,1967(1):310-322.
[7]Demsey J P ,Sinclair G B.On the stress singularities in the plane elasticity of the composite wedge[J].Journal of Elasticity,1979,9:373-391.
Stress singularity of flexible joint in combined material interface corner
AN Chun-li1,REN Quan-bin1,WANG Tie-jun2,ZHAO Gui-ping2
(1.The 41st Institute of the Fourth Academy of CASC,Xi'an 710025,China;2.Xi'an Jiaotong University,Xi'an 710049,China)
On basis of the mechanics of interface,singular stress field of interface corner created by reinforcement and elastomer of flexible joint was established.According to interface continuous condition and free boundary condition,the linear equation group of characteristic value λ which is related to the singular stress field was obtained.Then,singular stress field and displacement field which include stress intensity coefficient in interface corner of flexible joint were found through solving equation group and deducing formula.At the same time,based on the range of λ value,the selection of reinforcement and elastomer as well as geometrical angle with the stress singularity disappearing were presented.The results of singular stress field gained from calculation and finite element method verify the correctness of the analytical solution in this report.
flexible joint;stress singularity;interface corner;characteristic value;stress intensity coefficient
V435
A
1006-2793(2012)03-0391-05
2011-11-07;
2012-03-09。
安春利(1971—),男,博士,主要从事固体火箭发动机的喷管研究。
(编辑:薛永利)

