基于傅立叶平均法下的连续小推力动力学分析①

冯维明，李 源，苗 楠

(山东大学 工程力学系，济南 250062)

基于傅立叶平均法下的连续小推力动力学分析①

冯维明，李 源，苗 楠

(山东大学 工程力学系，济南 250062)

通过将小推力展开为偏近点角的傅立叶级数，并对高斯摄动方程在一个轨道周期上的平均，将原方程的推力转化为仅由14个傅立叶系数表示的控制变量。仿真计算表明，平均化后的高斯方程使计算量与牛顿积分相比显著减少，且对小推力而言有足够的精度。对利用平均化后的高斯方程计算轨道根数时产生误差的原因进行了研究，并进一步分析小推力的范围和小推力近似表达式对上述误差的影响，为今后小推力下非开普勒轨道动力学分析提供了理论依据和参数。

傅立叶级数;连续小推力;平均法;高斯方程;动力学分析;非开普勒轨道

0 引言

小推力推进系统为许多星际航行和地球轨道任务提供了一种高效的新选择，但是这种系统却对最优化控制提出了新的挑战［1］对于某些特殊的小推力作用的情况下，轨道转移的最优控制问题已经出现了解析法和数值近似解的方法［2-3］，但是对于一般的小推力问题，需要对每一个初始条件和推力值进行完整的数值积分，轨道参数的确定往往对这些变量很敏感。因此，普通的最优控制法则对于确定螺旋轨道的数十甚至上百圈轨道是十分困难的［4］。

在一些特殊情形的轨道转移中，数值解法已经得到了挖掘。目前较多的解法应用了变分法或直接优化法［5-7］，以确定特定约束条件下的小推力的最优控制律。此外，文献［8］运用李亚普诺夫反馈控制的方法，用以解决开环轨道最优时间控制和最优轨道问题。然而实践证明，把平均法和其他方法结合的思路在解决对初始轨道和推力变量预测敏感的问题上是很有效的［9-10］，但所有这些方法都局限于特定的推力和轨道参数范围。

本文讨论了一种有效解决航天器在小推力下轨道动力学问题的新方法。推力加速度的各分量以偏近点角展开为傅立叶级数，而高斯变分方程则在一个轨道周期上进行平均并且通过正交条件进行简化，从而定义出了一组久期方程。这组久期方程是一个含有14个推力傅立叶系数的函数(无论初始傅立叶级数的阶数是多少)。因此，该方法将普遍形式的推力分布情况简化为仅有14个参数的形式，这使计算量与牛顿积分相比大大减少。并以此分析了影响傅立叶系数表示的平均久期方程求解精度的主要因素。

1 数学建模

考虑一个在轨航天器，其质量对于其环绕的中心体可忽略不计。将航天器认为是一个质点。它受一个大小和方向可能随时间变化的连续推力加速度的作用。其轨道可用牛顿运动方程来表述:

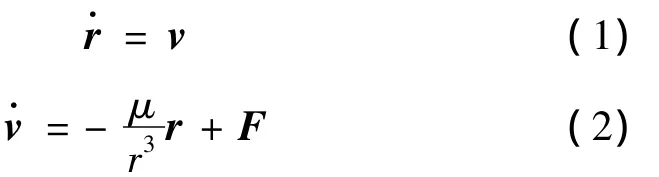
力加速度矢量F可以沿着径向FR、法向FW和周向FS分解，即

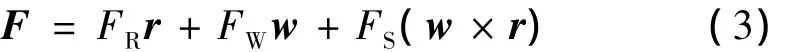
式中r和w分别为径向和法向的单位矢量。

牛顿方程可分解为拉格朗日行星方程，高斯形式的拉格朗日行星方程可表示为

式中 a为半长轴;e为偏心率;i为轨道倾角;Ω为升交点赤经;ω为近地点幅角;f为真近点角;E为偏近点角，而ε1+∫ndt=l为平黄经。

平近点角是平黄经和近地点幅角的差值:

根据傅立叶理论，对于任何一个在(0，L)上只存在有限个跳跃间断点的分段光滑的函数f(θ)，都可以表示为一系列周期性延伸的傅立叶级数，这个级数无限逼近于函数本身，当跳跃间断点存在时，傅立叶级数将逼近于左右极限的平均值。因此，这种表示方法可以应用于几乎任何一种普通的小推力航天器的控制律中。对于给定的任意加速度矢量F，其各个分量都可以展开为任意时间间隔上的傅立叶级数。实际上，傅立叶级数可按时间展开，也可按随时间变化的轨道参数展开，如真近点角、偏近点角或平近点角。考虑一个轨道周期L=2π，以θ来表示这一任意的轨道参数:

现在开始一阶平均化分析，先假设一个加速度矢量，它可在一个轨道周期(L=2π)中表示，这个加速度矢量的数值足够小，以使轨道的大小和形状在一圈中的改变不是很明显。因此，可将高斯方程相对于平近点角在一个轨道周期上平均来得到平均轨道根数。

式中 γ代表任意的轨道根数。

在对推力加速度矢量的各分量进行傅立叶展开时，所使用的轨道参数的选择是很重要的，有的参数会使由此得出的久期方程将变得冗长而复杂(如按真近点角展开成傅立叶级数的话)，而有的参数会使久期方程会被简化。经比较，加速度矢量的每一个分量都是按偏近点角进行傅立叶级数展开是最佳选择，并且各轨道参数的平均化也是按偏近点角进行，由dM=(1-ecosE)dE，式(13)可写为

将式(11)代入式(4)～式(9)中，并由式(14)可得到关于偏近点角的平均化高斯方程。由傅立叶级数的正交性，可消掉推力加速度傅立叶展开级数中第二阶以上及个别第二阶傅立叶系数。因此，无论初始推力加速度傅立叶级数的阶数如何，轨道根数a、e、i、Ω、ω和ε1的平均变化率只与这14个傅立叶系数有关，即(k=0，1，2)(k=0，1，2)(k=0，1，2)，(k=1，2)(1，2)则高斯平均方程为

2 计算分析

为在计算时数据的简便起见，将方程做归一化处理。在此，将重力参数μ归一化常数，μ=3.986×105km3/s2=3.986×1014m3/s2，因此相当于各变量的长度(以m为单位)除以。初始的轨道根数由表1给出。

表1 初始轨道根数Table 1 initial orbit elements

设控制率为周向加速度FS=1×10-8×(1-sinE)、径向加速度FR=1×10-8×sinE、法向加速度FW=1×10-8×(1+cosE)，上述推力的加速度分量为归一化后的值，如航天器为1 000 kg，推力的最大值幅值为2.208 N，可算作小推力范围。用龙格-库塔法进行积分来估算轨道根数的变化情况。该情况下由牛顿方程和平均变分方程求解出的轨道根数分别用实线和虚线在图1中给出。

图1 航天器受到3个方向推力加速度作用时轨道根数吻合情况Fig.1 Osculating orbital elements of spacecraft subject to acceleration in three directions

由图1可看到，所有的轨道根数均给出了非常吻合的结果。即用傅立叶系数表示的平均久期方程的求解结果和直接对拉格朗日方程进行积分得到的结果具有紧密的一致性。

再考虑一个简单的周向分步加速度的问题，FR=FW=0，FS按如图2中所示变化。每个周期中包含2次点火和2个滑行弧，初始轨道同表1所示。切向分步推力加速度作用时轨道根数吻合情况见图3。

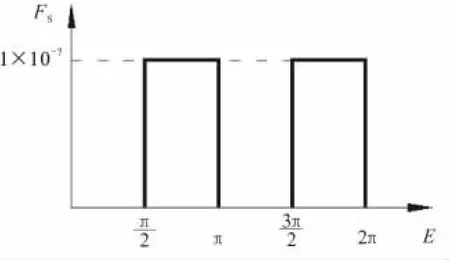
图2 周向分步加速度Fig.2 Step tangential acceleration

图3 切向分步推力加速度作用时轨道根数吻合情况Fig.3 Osculating orbital elements of spacecraft subject to step tangential acceleration

由图3知，平均久期方程和牛顿方程给出的结果具有完全相同的趋势，数值上也相差不大。

另外，基于傅立叶平均化后的高斯方程最显著优势之一就是计算量大规模减少，尤其在进行非开普勒轨道优化计算时，计算精度和计算耗时是困扰着众多学者的问题，考虑在表2所列初始条件下，归一化后的周向推力为FS=5×10-9(实际推力加速度为7.36×10-5m/s2)，分别用牛顿方程和平均变分方程求解出的轨道根数及误差列入表2。

推力表达式为如下形式:

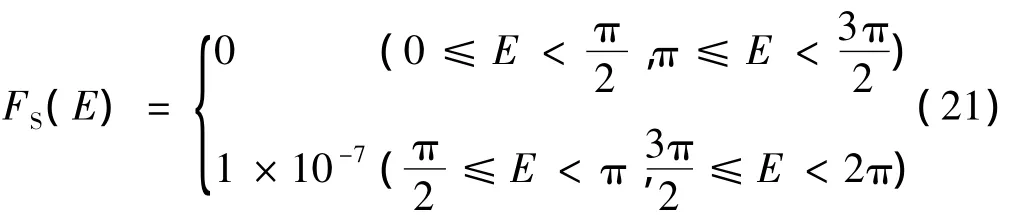
表2 连续小推力作用下牛顿方程和平均方程10圈后的计算结果比较Table 2 Comparison of the calculated results determined by the two methods on low-thrust continuous controls after running 10 laps

航天器运行时间为65 973.4 s，约运行10圈。由表2计算结果看出，由平均化后的高斯方程计算得到的10圈后的轨道的6个根与牛顿方程精确积分所得到的结果相比，除近地点幅角ω相对误差略大些，其他相对误差非常之小。利用牛顿法进行精确积分计算耗时(CPU耗时)为13.556 407 s，而利用基于傅立叶平均化后的高斯方程计算耗时为0.450 808 s，后者比前者快30倍。

3 影响计算精度的主要因素

平均久期方程能够精确有效解决小推力螺旋轨道问题，且与通常的牛顿问题的积分方法相比能大大减少计算量。但每一种近似计算方法都有其局限性，对于平均久期方程也是如此，这也是很多文献所未曾涉及到的问题，因此很有必要对利用该方法进行轨道计算可能导致的精度进行分析。

3.1 推力幅值大小的影响

由该方法的限制条件可知，推力幅值过大，会导致周期内轨道变形太大，从而使平均法的结果产生累计误差，于是，关心在保证精度条件下，推力的极限值是多少。为讨论推力增大对计算结果带来的影响，研究推力加速度大小在切向分步加速度形式(如图2示)的控制率中对计算结果的影响。令周向加速度FS的幅值分别增大为 1 ×10-7(归一化后)的 1.0、1.5、2.0和2.5倍，限于篇幅仅讨论对轨道形状影响最大的根数解半长轴a和偏心率e，图4给出其吻合情况(幅值为1×10-7见图3)。

图4 不同切向分步推力加速度作用时轨道根数吻合情况Fig.4 Osculating orbital elements of spacecraft subject to different step tangential acceleration

为更清晰地表现牛顿方程与平均方程的计算结果误差，现将不同幅值的推力作用下航天器运行20圈2种方法计算得到的半长轴a、偏心率e及相对误差列入表3。

由图4和表3可看到，随着加速度幅值的增大，a和e的误差都在增大，a的误差增幅较小，而e的误差显著增大。在FS达到2.5×10-7时，偏心率的2种求解结果已有显著偏离，此时对应质量为1 000 kg的航天器，推力大小约为18.4 N，约20圈后，偏心率的结果已经完全不可靠了。另外，由图4也可看到，即使推力较大时，在前12圈之内，平均久期方程和牛顿方程给出的结果仍然保持着良好的一致性。由表3可见，半长轴变化很大，因此，若在一定圈数内完成变轨任务，平均方程仍有足够的可靠度，即小推力的上限应根据变轨任务确定。

表3 推力加速度大小对a、e计算误差的影响Table 3 Influence of acceleration on the accuracy of a and e

3.2 近似推力表达式的影响

由式(15)～式(20)可知，平均化后的高斯方程仅与14个傅立叶系数有关，推力的傅立叶级数高阶项会因平均过程而被消去，平均化后非零的傅立叶系数是否能精确的描述原推力形式将成为关键。在本文第1个算例中，由傅立叶系数表达式(12)不难得到各推力加速度矢量分量的傅立叶表达式中的系数为=1 ×10-8=1 ×10-8=-1 ×10-8=1 ×10-8和=1×10-8，而其他系数均为零。将上述非零系数带入式(11)可得

高斯方程经平均化后得到的推力加速度分量傅立叶级数近似表达式与原初始推力表达式完全一致，因此傅立叶级数近似表达式对计算精度没有影响。下面再来考虑3个推力分量皆为分步加速度的形式，即

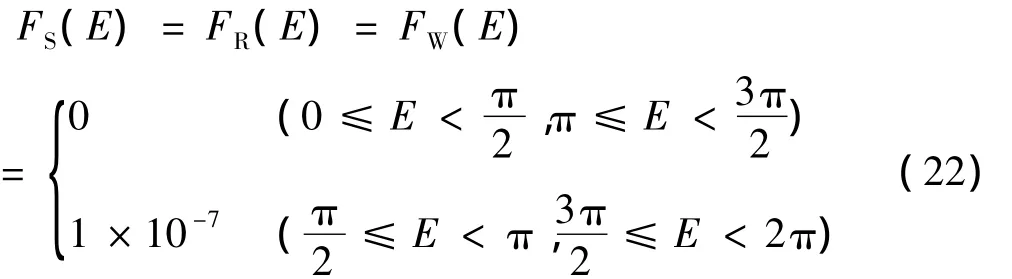
在图5中可表示加速度分量近似表达式与原表达式的差异。图5中用点表示的线是高斯方程平均后3个加速度分量变化曲线，注意到此时径向推力FR已变成常数，为分段推力的平均值;而周向推力FS和法向推力FW近似为正弦函数形式，从图形上看比较接近原推力形式。这也就是在前例中(仅有周向推力FS)计算精度较高的原因之一。平均方程与解析解得到的计算结果如图6所示。

图5 分段切向加速度的傅立叶级数表示Fig.5 Fourier series for step circumferential acceleration

图6 三向分步推力加速度作用时轨道根数吻合情况Fig.6 Osculating orbital elements of spacecraft subject to step circumferential acceleration in three directions

图6表示的是航天器运行了10圈的根数时程图。长半轴a和偏心率e平均方程的解与牛顿积分法的解吻合的较好，轨道倾角i，升交点赤经Ω，近地点幅角ω在10圈后误差开始增大，较明显的为Ω的值，平均结果开始偏离高斯方程积分结果。

4 结论

(1)将推力加速度分量展开为偏近点角表示的傅立叶级数，而高斯变分方程则在一个轨道周期上进行平均并且通过正交条件进行简化。该方法将整个连续控制问题的参数减少为14个(无论初始傅立叶级数的阶数是多少)，这使计算量与牛顿积分相比大大减少。

(2)通过平面变轨和空间变轨的计算结果分析，用该方法计算连续和非连续小推力下的轨道转移是正确的和准确的。

(3)对造成计算误差的主要因素进行了定性和定量分析，推力超出“小推力”的范围和傅立叶级数下推力的近似表达式(高斯方程平均后)是影响精度的主要因素，即便如此，在一定范围内平均法计算结果仍与牛顿方程的计算结果吻合良好。

［1］Gao Y.Advances in low-thrust trajectory optimization and flight mechanics ，dissertation thesis［R］.University of Missouri-Columbia，2003，64-12(B):6178.

［2］Craig A Kluever.Direct approach for computing near-optimal low-thrust earth-orbit transfers［J］.Journal of Spacecraft and Rockets，1998，29(1):45-61.

［3］Akella M R，Broucke R A.Anatomy of the constant radial thrust problem［J］.Journal of Guidance，Control，and Dy namics，2002，25(3):563-570.

［4］李俊峰，龚胜平.非开普勒轨道动力学与控制［J］.宇航学报，2009，30(1):47-53.

［5］Kluever C A.Optimal low-thrust interplanetary trajectories by direct method techniques［J］.Journal of the Astronautical Sciences，1997，45(3):162-247.

［6］Petropoulos A E.Some analytic integrals of the averaged variational equations for a thrusting spacecraft［R］.Interplanetary Network Progress Rept.42-150，Jet Propulsion Lab.，California Inst.of Technology，Pasadena，CA，Aug.2002:1-29.

［7］John T Betts.Very low-thrust trajectory optimization using a direct SQP method［J］.Journal of Computational and Applied Mathematics，2000，120:27-40.

［8］Gurfill P.Nonlinear feedback control of low-thrust orbital transfer in a central graviational field［J］.Acta Astronautica，2007，60(8-9):631-648.

［9］Jennifer S Hudson，Daniel J Scheeres.Reduction of lowthrust continuous controls for trajectory dynamics［J］.Journal of Guidance，Control，and Dynamics，2009，32(3):780-787.

［10］尚海滨，崔平远，栾恩杰.基于平均法的小推力转移轨道优化研究［C］//25届中国控制论文集.2006.

Dynamic analysis of continuous low-thrust based on fourier average method

FENG Wei-ming，LI Yuan，MIAO Nan
(Department of Engineering Mechanics，Shandong University，Jinan 250062，China)

Each component of the thrust vector was expanded as Fourier series in eccentric anomaly and Gauss variational equations were averaged over one orbit period，then the thrust vector was translated to a variable controlled by fourteen Fourier＇s parameters.Simulation results show that these secular equations are sufficient to accurately determine a low-thrust spiral trajectory with significantly reduced computation as compared with integration of the full Newtonian problem.In addition，error causes of orbit elements witch were calculated by the averaged Gauss equations were studied，and influence of low-thrust range and approximate expressions on the error was further analyzed，providing theoretical basis and parameters for dynamic analysis of the Non-Keplerian orbits of lowthrust.

Fourier series;continuous low-thrust;average method;Gauss equations;dynamic analysis;non-Keplerian orbits

V412

A

1006-2793(2012)03-0285-05

2011-08-18;;

2011-10-10。

国家863项目。

冯维明(1957—)，男，教授，主要研究方向为非线性动力学和轨道动力学。E-mail:fwm@sdu.edu.cn

(编辑:吕耀辉)