基于特征参数的吸气式高超声速飞行器上升段轨迹优化①
丁洪波,蔡 洪
(国防科技大学航天与材料工程学院,长沙 410073)
基于特征参数的吸气式高超声速飞行器上升段轨迹优化①
丁洪波,蔡 洪
(国防科技大学航天与材料工程学院,长沙 410073)
针对吸气式高超声速飞行器上升段轨迹优化问题,提出并研究了基于特征参数的轨迹优化方法。首先,建立了吸气式高超声速飞行器动力学模型,给出了气动力和推力模型。根据上升段轨迹特性,建立了基于指数函数和多项式的控制变量的取值模型。该模型取决于若干特征参数,从而将一个求解泛函的最优控制问题转化为求解特征参数的非线性规划问题,并采用序列二次规划算法求解。针对初值敏感性,提出了基于遗传算法的初值选取方法,以及基于物理意义的手动选取方法。
吸气式高超声速飞行器;上升段;特征参数;轨迹优化;初值选取
0 引言
吸气式高超声速飞行器(AHFV)是未来最有可能实现高超声速单级入轨和高超声速巡航飞行的飞行器,它代表了未来航空航天领域的研究发展方向。这类飞行器所采用的超声速燃烧冲压发动机性能与马赫数、高度等飞行状态密切相关,且发动机余量较小。因此,必须对上升段飞行轨迹进行优化。
Buren和Mease[1]建立了单级入轨飞行器动力学模型,采用了轨迹优化软件OTIS进行了优化,得到上升段飞行轨迹。Corban和Calise[2]采用能态近似法和奇异摄动方法,在若干假设简化条件下,设计了一种次优的轨迹优化与制导方法。Lu Ping[3]采用动态逆的思想设计了空天飞机的上升段轨迹。该飞行器的飞行任务是进入地球轨道,发动机采用吸气式发动机和火箭发动机组合方式。吸气式发动机主要在稠密大气中作用。吸气式发动机的风门系数采用三次多项式拟合,并采用参数优化的方法求解未知量。Keshmiri[4]建立了简化形式的吸气式飞行器上升段动力学方程,借鉴直接法的思想采用MATLAB工具箱进行了轨迹优化。Park[5]以及宗群[6]等使用伪谱法进行吸气式超声速飞行器的上升段轨迹优化,设计了优化策略,并进行了纵向平面内的仿真计算。佘智勇等[7]采用间接法将上升段轨迹优化问题转化为两点边值问题,然后采用伴随方法进行求解。
综合前人的研究成果,在20世纪90年代,学者主要采用间接法,并借鉴奇异摄动的思想研究和求解AHFV的轨迹优化。近几年来,随着轨迹优化方法的发展以及计算机硬件水平的提高,直接法特别是伪谱法得到了广泛应用,并取得较好效果。
本文旨在对AHFV上升段轨迹进行优化设计,提出一种不同的轨迹优化方法。其特点是充分考虑AHFV上升段轨迹的特性,着重从工程应用的角度分析控制量的取值特性,在此基础上建立基于特征参数法的优化模型,并研究了相应的优化算法。
1 吸气式飞行器动力学方程
AHFV一般具有升力体外形,采用冲压发动机作为推力装置。因此,它在飞行过程中会受到推力和气动力的作用。AHFV的纵向运动方程为[8]

式中u为无量纲化速度;γ为当地速度倾角;z为无量纲化地心距;θ为航程;为无量纲化质量和为无量纲化阻力和升力为无量纲化推力;α为攻角。
实际的阻力和升力为D和L,则

式中q为动压;Sref为飞行器有效参考面积。
因为气动系数与攻角α有关,因此空气动力主要由α和q决定。
实际推力大小为

式中为最大推力系数;st为发动机风门系数,0≤st≤1;Se为引擎进气道面积。
推力大小主要由st和q决定。
综上所述,AHFV的控制量有2个:一个是风门系数st,它主要控制推力大小,当st=0时,风门关闭,推力为零,当st=1时,风门最大,推力为当前状态下所能得到的最大推力;另一个控制量是攻角α,它控制升力和阻力的大小。轨迹优化的目的是选取合适的st和α,在满足约束条件前提下,使性能指标最大或最小。
2 基于特征参数的轨迹优化模型
2.1 攻角取值模型
AHFV上升段轨迹与火箭上升段飞行轨迹有类似之处,所以可借鉴火箭上升段大气层内转弯部分轨迹设计方法。火箭上升段攻角一般采用下式[9]:

攻角变化规律参见图1。开始迅速地达到负极值,然后绝对值开始变小,以指数速率趋于零,趋于零的速度由参数a决定。
火箭一般采用垂直起飞方式,需采用负攻角转弯。AHFV在发动机工作阶段攻角必须大于零,同时考虑到其初始攻角不一定为零,AHFV攻角模型可采用下述表达式:

式中tc为时间的无量纲量。
图1给出了火箭与AHFV的攻角模型,二者的区别主要是火箭攻角由零减小,然后又增大,趋近于零;AHFV的攻角则在初始时刻有一不小于零的值,然后增大至最大值,然后又趋近于初始值。

图1 火箭与AHFV攻角模型比较Fig.1 Attack angle models for rocket and AHFV
2.2 风门系数取值模型
对于AHFV而言,风门系数大小可调整,风门系数可取为三次多项式模型[3]。

假设初始时刻t0和终端时刻tf的油门系数大小及其变化率分别为cT0、cTf、˙cT0、˙cTf,则
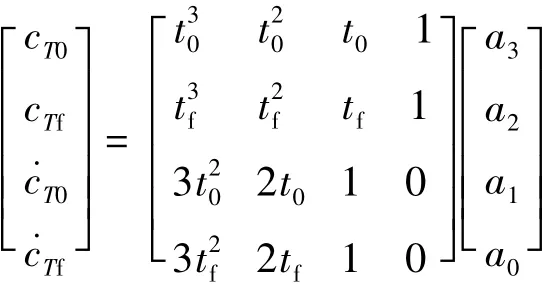
根据上式,可求出三次多项式的系数。

式(6)中待确定的参数为cT0、cTf、˙cT0、˙cTf,以及终端时刻tf。
需注意的是风门系数的大小是有约束的,其值在[0,1]之间。针对这个约束,一般的处理方式是直接采用式(7)[3]。

本文通过对式(7)的分析,将针对cT的约束转化为对待优化参数cT0、cTf、˙cT0、˙cTf的约束,使问题得到简化。
式(7)等效于
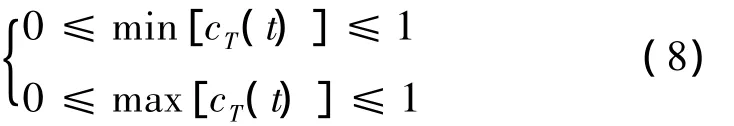
即cT的最大或最小值均为0和1之间。对式(5)求导,即
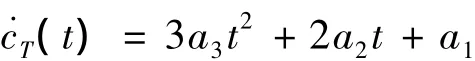
当a3=0时

对应的极值为2

当a3≠0,且-12a3a1≥0 时,cT在[0,1]之间存在2个极值。

当a3≠0,且-12a3a1≥0 时,cT在[0,1]之间无极值。
综上所述,要满足式(7),只需有式(13)即可:
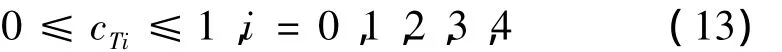
其中,cT4=cTf。
2.3 过程约束的处理方法
上升段飞行过程中,需考虑过载N以及动压q等过程约束。以动压约束q为例,本文采用如下方法处理过程约束。
引入变量ζ作为一个新的状态变量,使

用这种方法可将飞行过程中超出动压约束的点记录下来。于是,如果没有超过过程约束,则ζ(tf)=0,否则 ζ(tf)>0。
如果性能指标为燃料最省,也即

考虑动压约束后,引入新的性能指标:

其中,ν为常数,称为惩罚因子,可取为大于1的值。
2.4 优化模型与求解算法
至此,已将控制量α、st随时间的变化规律用若干具有一定物理意义的特征参数表示出来。根据初始状态以及控制量的值,即可对动力学模型积分,得到飞行轨迹。根据状态量和控制量的值,可判断轨迹是否满足约束条件,并结合性能指标函数的值,采用迭代寻优的方法来求取最佳的特征参数。这就是基于特征参数的积分方法的基本思想。
该方法的优化模型如下:

式中f代表动力学模型;x为状态变量;φ为终端约束条件。
式(16)描述的优化问题的实质是一个非线性规划问题,可采用序列二次规划(SQP)算法求解。与其他优化算法相比,SQP具有收敛性好、计算效率高、边界搜索能力强等特点,且能有效处理含约束问题。但该算法需首先给定参数的迭代初值,迭代初值的好坏直接影响着算法的性能,如果初始不好,还可能导致得不到优化结果。
3 优化初值的求取方法
本章提出2种优化初值的求取方法,包括遗传算法和基于物理意义的手动选取方法。
3.1 遗传算法
遗传算法(GA)的优点在于良好的全局寻优性能,且不存在初值敏感问题。这里提出“广义”可行解的概念,旨在解决遗传算法搜寻可行解困难的问题。
以二维解空间为例进行说明,如图2所示[10-11]。

图2 “广义”可行解的概念Fig.2 Concept of extended feasible solution
图2中,S1~S5代表了原优化问题的可行解集域,如果这些区域在整个解空间内分布较小且相隔较远,遗传算法的随机搜索机制难以保证在有限次遗传代数内使优化结果收敛于可行解集域。为了给后续的SQP算法提供1组较好的迭代初值,可适当放宽约束条件,如将等式约束改为不等式约束、将不等式约束的范围扩大,于是原优化问题转化为中间优化问题,其可行解集域为E,E内任一点即为原优化问题的“广义”可行解。显然,S1~S5均包含于E内,E的大小由约束条件的放宽程度决定。
但是,利用遗传算法求解上述优化问题存在明显缺陷:
(1)当解空间较大时,其概率性搜索的性质无法保证以足够的精度收敛到最优解;
(2)对约束的处理不如SQP灵活,内含两点边值问题,导致解集域不连续,故可行解的搜寻存在困难。
考虑到SQP算法具有很强的局部寻优能力,在一定程度上弥补了遗传算法精度不高的缺点。因此,可采用“GA+SQP”的组合优化算法求解轨迹优化问题,即首先利用遗传算法获得“广义”的最佳可行解,然后将此可行解作为SQP算法的迭代初值进行寻优计算。
3.2 基于物理意义的手动选取方法
在第2章对攻角模型及其表达式中各个参数含义进行了分析,可看到各个参数具有明确的含义。可根据各个参数对攻角模型的影响以及攻角对飞行轨迹的影响,采用手动方法(MM)来确定各个参数的初值。
下面分析各攻角模型中各个参数对轨迹的影响,见图3。
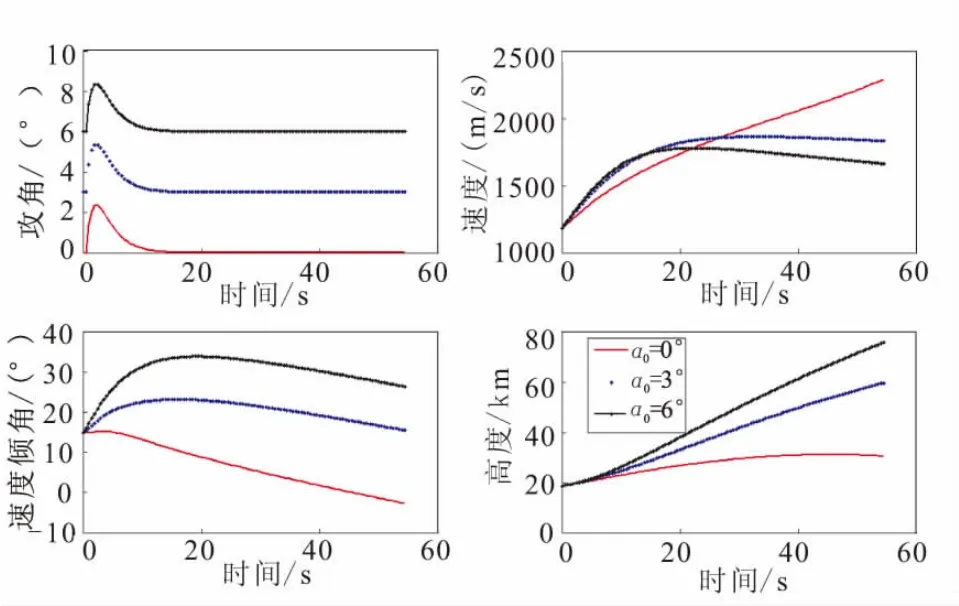
图3 α0对飞行轨迹的影响Fig.3 Effect of α0on trajectory
从图3可看到,增大α0会导致攻角增大。升力以及沿轴向的推力也较大,导致速度倾角增大,所以高度也会增大。
随着高度的增加,空气逐渐变稀薄,动压减小,导致发动机推力减小,推力减小到一定程度后,加速度将小于零,速度将减小。所以,当攻角较大时,速度会有一个先增加后减小的过程。
同理,速度倾角也有一个先增大后减小的过程。当速度倾角减到小于零时,高度会减小。图4给出了αm取值为 -2°、0°、2°时的攻角以及轨迹变化。

图4 αm对飞行轨迹的影响Fig.4 Effect of αmon trajectory
由图4可见,αm正、负不同时,攻角的变化规律相反。增大αm会增大攻角的峰值,相应的,速度倾角和飞行高度均会增大,而飞行速度会减小。
从图5可看到,增大a会缩短攻角由极值变化到α0的时间,a越大,α处于最小值的时间越长。当a>1时,基本可认为攻角一直取α0。所以,基本可认为a的取值范围为[0,1]。
采用类似方法,也可分析风门系数表达式中4个待定参数对飞行轨迹的影响,从而可通过手动调整的方式逐步给出各个参数的初始值。
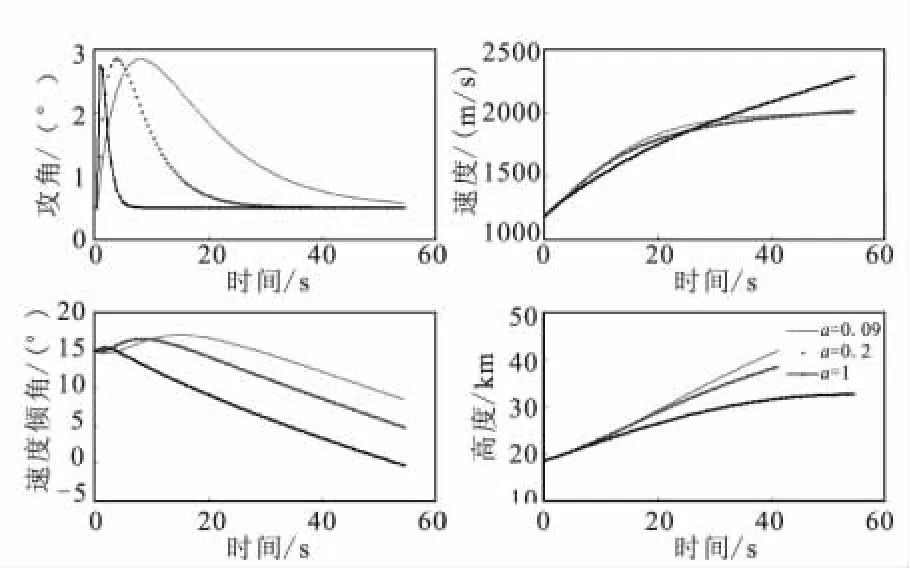
图5 a对飞行轨迹的影响Fig.5 Effect of a on trajectory
4 仿真算例
AHFV模型参见文献[12],初始高度为15 km,初始马赫数为4,航迹角为15°,要求终端高度为30 km,终端马赫数为6,终端航迹角为0°。
在求取初值的过程中,可将相关约束项放宽为

表1和表2分别给出了由GA和MM方法得到的初始值,以及用这些初始采用SQP算法得到的优化结果。从表1和表2可看到,2种方法所给出的初始不尽相同,而以这2个初始得到的最优优化结果也是不同的,这也从另一个侧面说明了SQP算法对初始值的敏感性。

表1 “GA+SQP”算法优化结果Table 1 Optimal results of the‘GA+SQP’method

表2 “MM+SQP”算法优化结果Table 2 Optimal results of the‘MM+SQP’method
图6和图7给出了2种方法得到的轨迹以及相应的控制量。从图6和图7可看到,2种方法得到的控制量是不相同的,轨迹变化过程也不相同,但2种方法得到的轨迹均满足约束条件。从性能指标上看,二者差别也不大,采用GA+SQP算法结果略优于MM+SQP算法的结果。

图6 2种方法得到的优化轨迹Fig.6 Optimal trajectories of the two methods

图7 2种方法得到的控制量Fig.7 Optimal controls of the two methods
5 结论
(1)对吸气式高超声速飞行器上升段轨迹进行了优化设计。针对攻角和风门系数,分别建立了基于特征参数的取值模型,从而得到以这些特征参数为优化变量的参数优化模型。
(2)着重分析了优化初值的选取方法,采用GA+SQP算法和MM+SQP分别进行了仿真计算,得到满足条件的优化结果,说明了方法的有效性。
[1]Mark A Van Buren,Kenneth D Mease.Minimum-fuel ascent to orbit using air-breathing proplusion[R].NASA Report,1992:54-58.
[2]Corban J E,Calise A J,Flandro G A.Optimal guidance and propulsion control for transatmospheric vehicle[C]//AIAA Guidance,Navagation and Contrl Conference.August 14-16,1989:123-130.
[3]Lu Ping.An inverse dynamic approach for trajectory optimization and guidance for an aerospace plane[R].AIAA 92-4331-PC:217-223.
[4]Shahriar Keshmiri,Richard Colgren.Trajectory optimization for a generic hypersonic vehicle[C]//AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference,2006:1-8.
[5]宗群,田苓,窦立谦.基于 Gauss伪谱法的临近空间飞行器上升段轨迹优化[J].宇航学报,2010(7):1776-1781.
[6]佘智勇,马广富,沈作军.基于间接伴随法的大气层内高超声速飞行器最优上升轨迹研究[J].宇航学报,2010(8):1951-1957.
[7]Jung-Woo Park,Min-Jea Tahk,Hong-Gye Sung.Trajectory optimization for a supersonic air-breathing missile system using pseudo-spectral method[J].Int.J.of Aeronautical &Space Science,2009,10:135-138.
[8]阮春荣.大气中飞行的最优轨迹[M].北京:宇航出版社,1987:30-33.
[9]贾沛然,陈克俊,何力.远程火箭弹道学[M].长沙:国防科技大学出版社,1993:217-230.
[10]陈国良,王熙法.遗传算法及其应用[M].北京:北京人民邮电出版社,1996.
[11]胡正东,沈荟萍,张士峰,等.SGKW轨道在线生成技术研究[J].固体火箭技术,2009(7):191-195.
[12]Chuang C H,Hitoshi Morimoto.Optima periodic cruise for a hypersonic vehicle with constraints[R].AIAA 96-3876:321-325.
A characteristic parameter trajectory optimization method for the ascent phase of the air-breathing hypersonic flight vehicle
DING Hong-bo,CAI Hong
(College of Aerospace and Material Engineering ,National University of Defence Technology,Changsha 410073,China)
A Characteristic Parameter Trajectory Optimization Method(CPTOM)for the ascent phase of the air-breathing vehicle was proposed and studied.The expression for aerodynamic force and thrust were specially studied,and the motion equations were founded.According to the characteristics of the ascent motion of air-breathing hypersonic flight vehicle(AHFV),the control variable models based on exponential and polynomial functions were established.The models were determined by several characteristic parameters to be optimized.So the optimal control problem was translated to a nonlinear programming problem which can be calculated by the Sequence Quadric Programming(SQP).Because of the sensitivity of the initial value for optimization,the Genetic Arithmetic(GA)and Manual Method(MM)were proposed for initial value guess.
air-breathing hypersonic flight vehicle;ascent phase;characteristic parameters;trajectory optimization;initial value guess
V474.28
A
1006-2793(2012)03-0296-05
2011-10-14;
2011-11-21。
丁洪波(1982—),男,博士生,研究方向为轨迹优化与制导。E-mail:whhplz2000@sohu.com
book=35,ebook=118
(编辑:崔贤彬)

