解剖算子及其一致有界定理

刘 铁，郑 亮

(1.安康学院数学系，陕西安康 725000;2.哈尔滨工业大学 深圳研究生院，深圳 518055)

1 预备知识

闭图像定理、开映射定理和等度连续定理是泛函分析的三大基本原理。上述经典泛函分析基本定理过分依赖线性算子，使其应用性受到很大限制，因而许多学者在研究包括某些非线性影射在内的更大的函数类上建立三大基本定理。尤其是李容录教授在解剖算子上进行的泛函分析基本原理拓展取得了重大进展。本文对解剖算子在实数空间上进行讨论，得出一些相关性质。

定义1［1-2］对 φ∈C(0)及 U∈N(X)，称 f:X→Y 为解剖算子，若 f(0)=0，且对 x∈X，u∈U 及|t|≤1，有 r，s∈C，使|r-1|≤|φ(t)|，|s|≤|φ(t)|，f(x+tu)=rf(x)+sf(u).记 Fφ，U(X，Y)为由 φ∈C(0)及 U∈N(X)确定的解剖算子全体。

关于解剖算子，有如下几个基本函数空间［3-5］:

3)S={f:f是定义在R上的无限可微的速降函数}，则由范数列k≥0，p，q∈N 使 S 成为局部凸的 Fréchet空间。

命题1 若 f∈Fφ，U(X，Y)，u∈U，|t|≤1，则有 s∈C，|s|≤|φ(t)|，使 f(tu)=sf(u)。

证明由定义 f(0)=0，取 x=0 和上述的 u，存在 r，s∈C，使|r-1|≤|φ(t)|，|s|≤ |φ(t)|，f(x+tu)=f(tu)=rf(0)+sf(u)=sf(u)。

命题2 若 f:X→Y 是线性算子，则 f∈Fφ，U(X，Y)，∀φ∈C(0)，U∈N(X)。

证明f:X→Y是线性算子(∀x，u∈X，t∈K，

则f(0+0)=f(0)+f(0)(f(0)=0。要使f(x+tu)=rf(x)+sf(u)，可令其减去式(1)，f(x+tu)-［f(x)+tf(u)］=(r-1)f(x)+(s-t)f(u)，只要|r-1|≤|φ(t)|，|s-t|≤2|φ(t)|即可

可令，s=t，r=1 即有|r-1|≤|φ(t)|，|s|≤|φ(t)|，f(x+tu)=f(x)+tf(u)=rf(x)+sf(u)，所以 f∈Fφ，U(X，Y)。

例1 若‖·‖:X→R 是半范，则对 φ(t)=t，‖·‖∈Fφ，X(X，R)。

证明对于x，u∈X及 t∈C，‖x‖ -|t|‖u‖≤‖x+tu‖≤‖x‖ +|t|‖u‖，所以有 s∈［-|t|，|t|］，使得‖x+tu‖ = ‖x‖ +s‖u‖，即对 φ(t)=t，‖·‖∈Fφ，X(X，R)。

例2 若(X，‖·‖)是半范空间，对任意连续线性算子T:X→Y定义连续的非线性映射为，则对

证明若 x∈X，u∈U，|t|≤1，则‖x+tu‖ =‖x‖ +s‖u‖，其中 s∈［-|t|，|t|］，所以 fT(x+tu)=而

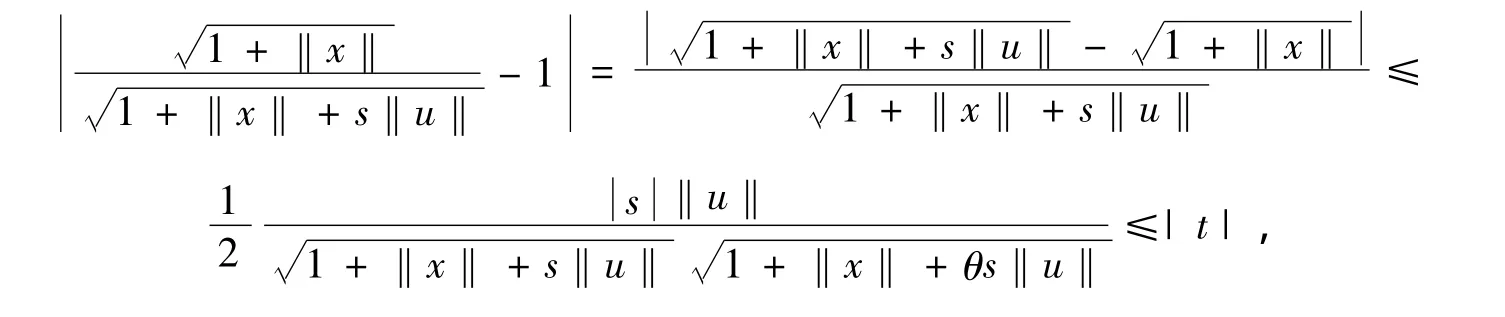
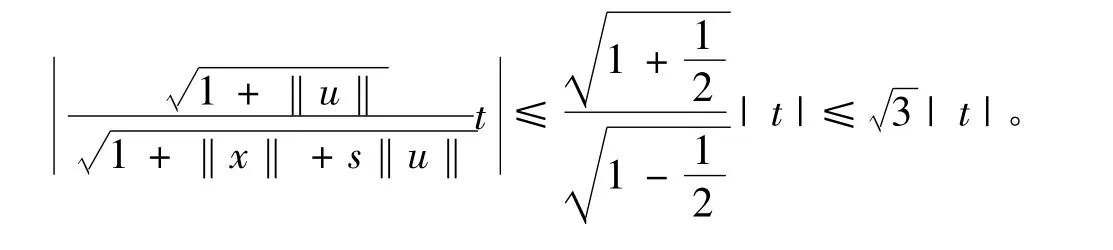
2 解剖算子的性质

(X，d)是可度量的拓扑线性空间，Fφ，U(X，Y)为由 φ∈C(0)及 U∈N(X)确定的解剖算子全体，记Bφ，U(X，Y)={f∈Fφ，U(X，Y):f(x)连续}，若 U={x∈X:d(X，0)＜ δ}，φ(t)=Ct，其中 C≥1，则记Fφ，U(X，Y)=FC，δ(X，Y)，Bφ，U(X，Y)=BC，δ(X，Y)，对 C≥1 及 δ＞ 0 记 EC，δ(X，Y)={f∈FC，δ(X，Y):对x，u∈X，d(u，0)≤δ及|t|≤1∃标量 s∈|s|≤C|t|，f(x+tu)=f(x)+sf(u)}

定理1 若 f∈Fφ，U(R，R)，则 f(x)连续，即 Bφ，U(R，R)=Fφ，U(R，R)。

证明有 δ＞0，使［-δ，δ］⊂U，设 x→x in R，∃N 当 n＞N 时

n，所以f(xn)→f(x)(n→∞)。

定理2 f∈Fφ，U(R，R)若 f≠0，则 f(u)≠0∀0≠u∈U。

证明假设0≠u∈U且f(u)=0任取0≠x∈R，取定n使得，存在 ri，si∈R(i=1，2，…，n)，使得，且

这与f≠0矛盾。定理2得证。

定理3 X为非平凡赋范线性空间，Y为非平凡线性空间，对于∀C＞1及δ＞0，集合{f∈FC，δ(X，Y):f是非线性的}为非可数集，其势不小于线性算子全体。

证明任取一个 η∈EC，δ(R，R)满足，则η定为非线性(因为线性的要么，要么

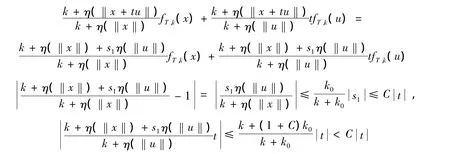
所以 fT，k∈FC，δ(X，Y)，定理 3 得证。

定理4 等度连续原理(Equicontinuity Principle)［6］X是第二纲的，Γ⊂Fφ，U(X，Y)是一族连续影射。若Γ在X上逐点有界即{f(x)|f∈Γ}有界，∀x∈X，则Γ在X上等度连续。

定理5 一致有界定理(Uniform Boundedness Principle)X是第二纲的，Γ⊂Fφ，U(X，Y)每一个f∈Γ连续，对{f(x)|f∈Γ}有界，∀x∈X，则 Γ 在有界集上一致有界，i.e.{f(x)|f∈Γ，x∈B}有界对每个有界集B⊂X。

证明设B⊂X有界，V∈N(Y)平衡，根据等度连续定理有平衡的U0∈N(X)使得U0⊂U，f(U0)⊂V，∀f∈Γ。取使，设

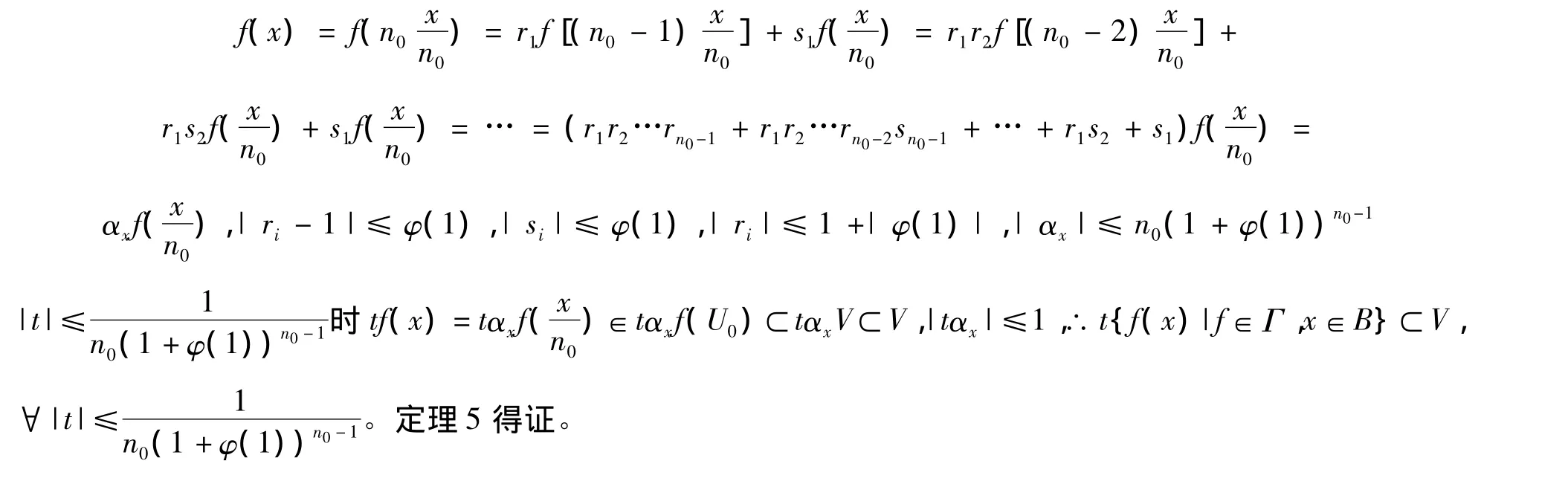
［1］Li Rong lu，Zhong Shuhui，Cui Chengri.New Basic Principles of Functional Analysis(Abstract)［J］.J of Yanbian Univ:Natural Science，2004，30(3):157-160.

［2］李容录，钟书慧，文松龙，等.泛线性广义函数(Ⅰ)［J］.延边大学学报:自然科学版，2007，33(3):157-159.

［3］Genlfand I M.Generalized Functions I［M］.New York:Academic Press，1964.

［4］Genlfand I M.Generalized Functions II［M］.New York:Academic Press，1964.

［5］Gelfand I M.Generalized Functions［M］.New York:Academic Press，1968.

［6］Li Rong lu.Equicontinuity in nonlinear analysis，to appear［Z］.