基于规范的高层建筑风与地震作用的简明对比

冷 元，范存新，唐和生

（1．苏州科技学院 江苏省结构工程重点实验室，江苏 苏州215011；2．同济大学 结构工程与防灾研究所，上海200092）

在高层建筑较多的地区，风载荷和地震作用都应在设计中重点考虑［1－2］，因此研究2种主要侧向载荷各在何时对结构的承载力起控制作用，使结构同时保证规范对抗震抗风设计要求就显得很有必要［3］，另外某些结构还须考虑人体舒适度问题［4－5］．洪小健等［6］对地震作用采用振型分解反应谱法计算，利用了载荷规范［7］给出的参考振型，计算较复杂，并且参考振型与实际有较大差别；余江滔等［8］的研究也只选择了某一类特定的结构形式；柯世堂等［9］对冷却塔进行了风振与地震作用比较研究．本文以苏南地区（苏州、无锡）为例，利用抗震规范［10］给出的底部剪力法计算由地震产生的结构基底剪力与基底弯矩，该方法忽略了高阶振型的影响，计算比较简便；给出了高层建筑顺风向振动与单向地震作用的比较方程，得到2种激励何时起控制作用的条件，使设计者无须对2种等效载荷同时在弹性范围内进行承载力验算，且未规定具体结构形式，因此具有普遍的参考价值．

1 风和地震等效载荷的计算

对于高层建筑，一般顺风向效应起着决定作用，因此本文在计算风对结构的作用时只考虑顺风向效应．我国规范常用平均风载荷乘上风振系数的方法计算在高度为z 处垂直于结构表面的顺风向单位面积上的总载荷：Wk＝βzμsμzW0，式中βz 为高度z 处的风振系数，μs 为风载荷体型系数，μz 为风压高度变化系数，W0为基本风压．根据载荷规范［7］42中的风振系数计算公式可以推导出高度为H 的结构顺风向等效载荷为

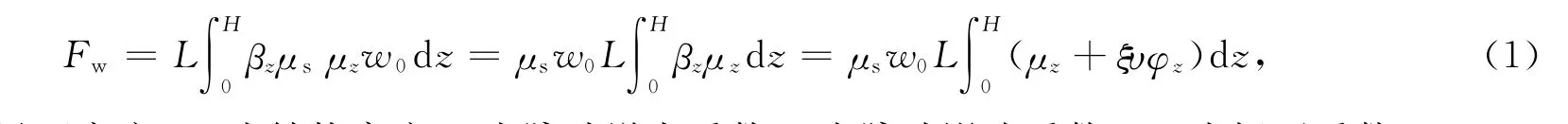
式中L 为迎风面宽度，H 为结构高度，ξ为脉动增大系数，υ为脉动影响系数，φz 为振型系数．

水平地震作用的计算主要有2种方法：①底部剪力法主要适用于高度不超过40m、以剪切变形为主且质量和刚度沿高度分布均匀的结构，只考虑第一振型的影响；②振型分解反应谱法则考虑了高阶振型的影响，实际上底部剪力法是振型分解法的一个简化，计算时采用集中质量法．振型分解反应谱法的计算精度高于底部剪力法，但须已知结构的自由度及各振型才能求解，本文研究的只是广义的建筑而非某一特定高层建筑，无法得知自由度的个数及振型，因此采用底部剪力法计算等效地震载荷．

按照抗震规范［10］35：FEk＝α1Geq，式中FEk为结构总水平地震作用标准值，α1为地震影响系数，Geq为结构等效总重力载荷，多质点可取总重力载荷代表值的85%．

2 比较方程的建立

风和地震都能使结构各截面产生剪力与弯矩，从力学上分析，基底截面又是结构剪力最大的截面，总作用载荷即为基底截面剪力，因此比较基底截面剪力与弯矩具有重要意义．本文主要建立基底截面在风和地震2种激励下剪力与弯矩的比较方程，并对方程中各参数的取值进行分析探讨．

结构基底截面剪力即为总作用载荷，可得比较方程

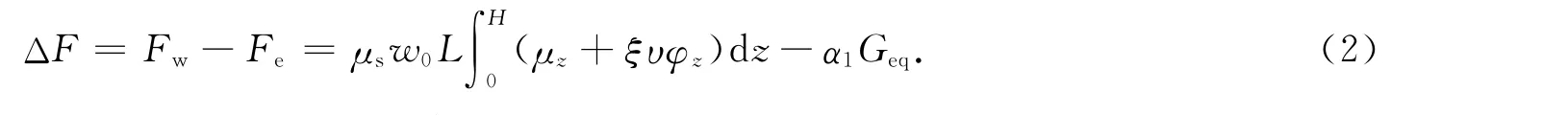
如果ΔF＞0，则表明风载荷占优；若ΔF＜0，则表明地震作用占优．结构顺风向风载荷作用下的等效基底弯矩为

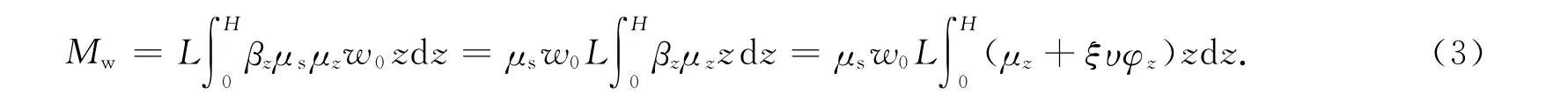
令Fi为质点i的水平地震标准值，则根据抗震规范［10］35：

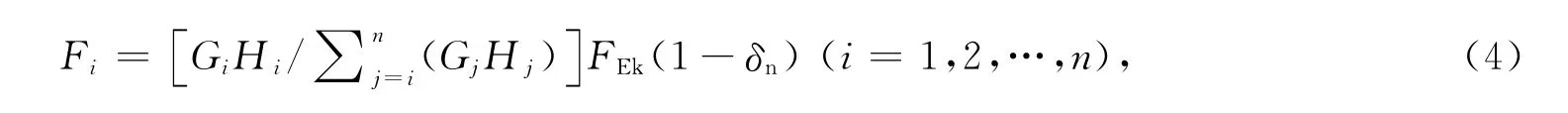
式中δn为顶部附加地震作用系数，本文研究的是高层建筑，可近似取0．根据式（4），用i质点所受的力乘上质点到基底的距离Hi然后求和，即可得到地震作用下结构的基底弯矩

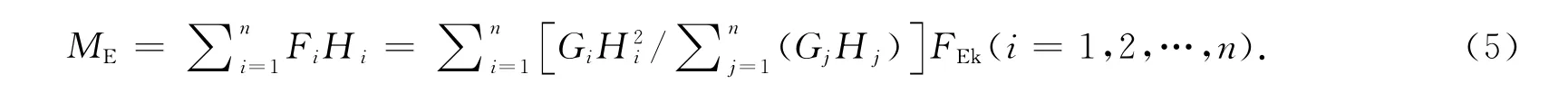
为了便于计算，现作如下简化与假定：每层层高相等，简化为1个自由度；根据相关规范规定：普通住宅层高宜为2．8m，办公楼的室内净高不得低于2．5m，而高层建筑主要为住宅、商务办公楼和酒店等，因此假定结构层高为3m；结构每层质量均匀分布，即计算时可假定每层质量相等．根据以上假定，｛Hj｝可视为公差为3、首项为3的等差数列，因此式（5）可进一步简化为

由式（3）和式（6）可得基底弯矩比较方程

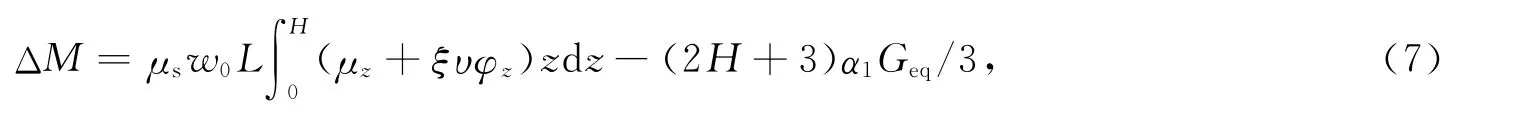
式中若ΔM＞0，则表明风载荷占优；若ΔM＜0，则表明地震作用占优．

3 比较方程中参数的取值与处理

3．1 结构参数取值

1）结构质量．本文主要研究的是矩形截面钢筋混凝土结构和钢结构，单位体积质量的钢筋混凝土结构取为400kg·m－3，钢结构取为300kg·m－3．

2）结构阻尼比．对于钢筋混凝土结构和组合结构，阻尼比通常为4%～6%，对于钢结构，阻尼比通常为3%～4%，因此阻尼比以钢筋混凝土结构为5%、钢结构为3．5%进行分析讨论是合理的．

许多国家都建议采用经验公式来估算结构自振周期［11－12］，本文采用的周期估算式为

3．2 基本风压与地面加速度峰值（地震影响系数最大值）

要比较风载荷和地震作用，必须首先确定2种载荷的最重要参数：风载荷的基本风压和地面加速度峰值．由于规范中给出某一地区的基本风压分别对应的重现期为10，50，100a，而通常采用重现期为50a的基本风压进行抗风设计，其年超越概率为2%．为了使比较有意义，必须使风载荷与地震作用的年超越概率大致相同．基本风压取值的年超越概率约为2%，而地面加速度峰值超越概率是50a内为10%．

地震危险性分析中各种地震发生概率模型应用最多的是泊松过程模型，其主要特点为平稳性、独立性和不重复性，因此可得到在使用期限［0，T］内发生n 次地震的概率为P（n）＝［（λT）k／n！］·exp（－λT），式中λ为地震的平均发生率．

假设某个时刻可能发生地震的地面加速度峰值为Ai，则地面加速度峰值A 全概率公式为P（A≤Ai）＝exp｛－［1－F（Ai）λT］｝，式中F 为某个时刻因发生地震而引起的地面加速度峰值所服从的分布函数．根据规范，以苏州为例，地面加速度0．05g的保证率为90%，则exp｛－［1－F（0．05g）50λ］｝＝0．90；因此，可以估算年保证率

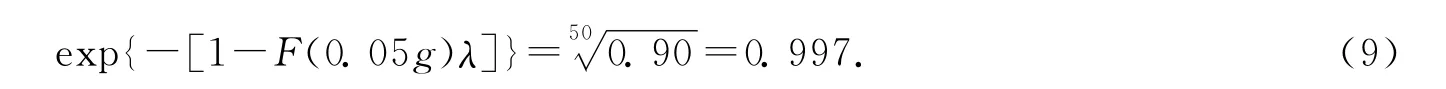
由式（9）可知超越概率为2．1%，另外地面加速度峰值A 与地震影响系数最大值αmax之间存在如下近似关系：A×0．775 2≈αmax．

由上述推导可以得知，苏南地区取规范给出的超越概率为2%的基本风压为0．45kN·m－2，地震影响系数最大值αmax取为0．04，即地面加速度峰值取为0．05g 进行对比分析是有意义的，这也再次证明了规范给定的基本风压和地面加速度峰值（地震影响系数最大值）是匹配的．

3．3 其他参数简化取值

矩形截面体型系数μs 取1．4．本文主要研究的是具有密集建筑群的大城市中的高层建筑，因此粗糙度类别为D，由载荷规范可知高度变化系数为μDz ＝0．318（z／10）0．60；脉动增大系数按照载荷规范相关规定线性插值后取值：钢筋混凝土结构取为1．252，钢结构取为1．950；脉动影响系数根据规范按表1取值．

表1 脉动影响系数取值Tab．1 The value of converting factor of gust wind

对于高层建筑，其振型系数计算近似公式为φz＝tan［4－1π（z／H）0．7］．利用Matlab软件绘制出φz 关于z／H的函数图像，如图1所示，可见其图像与直线y＝x的图像接近，因此可以近似认为φz 对z 的积分与z／H关于z 的积分相等．

特征周期Tg与所在地设计地震分组有关，本文研究城市的设计地震分组均为第1组，并且苏南地区地处长江中下游平原地区，场地土以Ⅱ，Ⅲ类土为主，另外Ⅳ类场地也不适合建大量高层建筑，因此本文主要研究Ⅱ，Ⅲ类场地，特征周期值分别为0．35，0．45s．

地震影响系数α1：由抗震规范给出的地震影响系数曲线可知，其函数表达式共分为4 段，而高层建筑高度最小为28 m，因此基本自振周期最小值由估算式可近似认为0．015 H ＝0．015×28＝0．42s＞0．1s，所以地震影响系数曲线只须考虑3段：

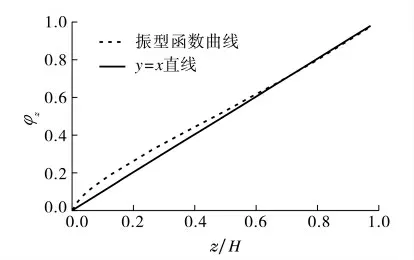
图1 振型系数曲线Fig．1 The curve of vibration mode

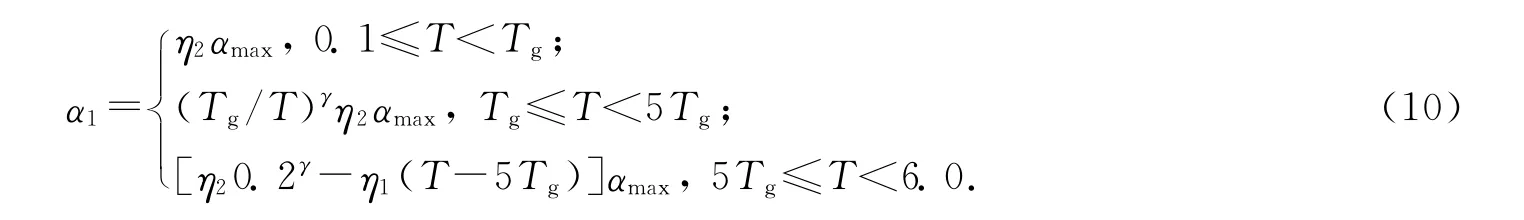
分别将ξ＝0．05，0．035代入式（10），可以得到钢筋混凝土结构与钢结构的地震影响系数．

4 计算结果

对式（2）或式（7），分别令ΔF＝0，ΔM＝0，则方程中只含H 与B 2个变量（脉动影响系数根据表1线性插值），对于给定H，则可求出相应的B 以及此时的高宽比（临界高宽比）．以Ⅱ类场地钢筋混凝土结构为例，将相关参数代入比较方程中可知剪力相等：B＝（0．009 25 H0．6＋0．116υ）／α1；弯矩相等：B＝（0．019 H1．6＋0．417υH）／［α1（2．27 H＋3．4）］．

同理可计算出对应于钢筋混凝土结构或钢结构在Ⅱ，Ⅲ类场地条件下2种载荷起控制作用的条件，如图2，3所示．

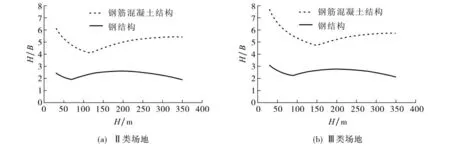
图2 结构基底剪力在风和地震作用下的H—H／B 关系曲线Fig．2 The curve of Hand H／Bto the base shear under the wind and earthquake action

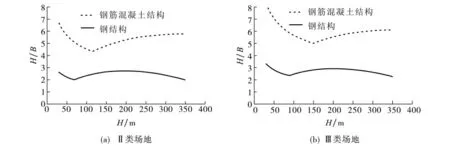
图3 结构基底弯矩在风和地震作用下的H—H／B 关系曲线Fig．3 The curve of Hand H／Bto the base moment under the wind and earthquake action

在图2，3中，若结构几何参数位于曲线上部，则基底剪力或弯矩由风载荷控制；若位于曲线下部，则由地震作用控制．

［1］ MAZZA F，VULCANO A．Control of the earthquake and wind dynamic response of steel－framed buildings by using additional braces and／or viscoelastic dampers［J］．Earthquake Eng Struct Dynam，2011，40（2）：155－174．

［2］ DUTHINH D，SIMIU E．Safety of structures in strong winds and earthquakes：multihazard considerations［J］．J Struct Eng，2010，136（3）：330－333．

［3］ ZHAO B，TAUCERA F，ROSSETTO T．Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China［J］．Eng Struct，2009，31（8）：1707－1723．

［4］ WILLEMSEN E，WISSE J A．Design for wind comfort in the netherlands：procedures，criteria and open research issues［J］．J Wind Eng Ind Aerodyn，2007，95（9／11）：1541－1550．

［5］ KWOK K C S，HITCHCOCK P A，BURTON M D．Perception of vibration and occupant comfort in wind－excited tall buildings［J］．J Wind Eng Ind Aerodyn，2009，97（7／8）：368－380．

［6］ 洪小健，顾明．基于规范的上海高层建筑风和地震作用的比较［J］．同济大学学报：自然科学版，2005，33（10）：1291－1296．

［7］ 中华人民共和国建设部．GB 50009—2001 建筑结构荷载规范［S］．北京：中国建筑工业出版社，2002．

［8］ 余江滔，陈统丹，陈建喜，等．设计中顺向风振与水平地震影响的比较［J］．四川建筑科学研究，2005，31（5）：94－98．

［9］ 柯世堂，赵林，葛耀君，等．烟塔合一冷却塔风振与地震作用比较研究［J］．武汉理工大学学报，2009，31（19）：70－72．

［10］ 中华人民共和国建设部．GB 50011—2010 建筑抗震设计规范［S］．北京：中国建筑工业出版社，2010．

［11］ KAUSHIK H B，RAI D C，EERI M，et al．Code approaches to seismic design of masonry－infilled reinforced concrete frames：a state－of－the－art review［J］．Earthquake Spectra，2006，22（4）：961－983．

［12］ AMANAT K M，HOQUE E．A rationale for determining the natural period of RC building frames having infill［J］．Eng Struct，2006，28（4）：495－502．