基于免疫—蚁群算法的应急物流配送网络优化研究

曹庆奎， 吴向儒， 车美林 （河北工程大学 经济管理学院，河北 邯郸 056038）

近几年来突发事件应急处理提升到一定的高度，应急物流系统开始得到学术界的重视。而配送问题是应急物流中的一个重要分支，所以应急物流配送网络优化问题的研究很有必要，其对提高应对突发事件能力和灾害应急管理水平有非常重要的意义。

对应急物流配送网络的优化问题，包括节点的优化及节点之间线路的优化，本文重点介绍应急物流配送路线的选择，实际上，将配送车辆的路径优化问题和应急物流结合起来研究有一定的难度，然而将二者统一的具体研究，更贴近目前物流系统复杂的实际特征，所以对它的研究很有价值。目前对于配送车辆路径优化的研究，多是以一般物流为基础，但是，应急物流与一般物流却存在着很多区别，例如：自然灾害等突发事件可能造成部分道路毁坏、信息不畅通、物资需求变动等，导致运输网络容量具有很大的不确定性；应急物流的配送车辆的路径优化问题主要是以时间效益最大化和损失最小化，而不是仅以成本最小化为目标，因此，应急物流配送车辆路径优化模型的目标、参数及约束条件与一般物流还是存在着一定区别的。国内外的相关文献大多分为关于运输时间最小化为目标的研究和关于运输成本最小化为目标的研究：Ae Young Choi研究了在路网情况不确定情况下如何分配有限的资源 （如救护车和其它应急救灾车辆）将受伤人员运输到医院，目标是使受伤人员存活数最大[1]。Gulay提出了一种分层多标准方法解决直升机在救灾中的调度问题，使派遣的直升机和飞行员数目在满足需求下成本最低[2]。国内的研究有计雷，池宏等研究员提出在突发事件中，物资运输的首要问题是研究尽快将物资运送到指定的灾害发生地，此时的运输问题变成了带时间约束的运输问题，目标函数不仅仅是成本最小化，更重要的是运送时间最小化。卢安文等人于2003研究了紧急情况下的物流配送的必要性，建立了考虑公路运输的紧急情况下的物流配送模型，并考虑多种运输方式，以时间、费用为目标建立了0-1整数规划模型及目标规划模型[3]。

目前研究中存在的问题：首先，以往研究较少涉及灾后沿街建筑倒塌、避难人群疏散及道路受损引起车辆运行时间的随机性等因素；多数文献中的模型参数大都是固定不变的，很少考虑到实际中车辆数、车场等这些随时变化的参数[4]；对应急物流配送网络的研究通常以一般物流为基础，这明显不符合实际：首先，在应急突发事件发生的情况下，配送中的车辆路线选择所考虑的影响因素明显不同于一般物流；其次，一般物流配送车辆的路径优化模型都是以成本最小化为单一目标，在重大突发事件发生的情况下，应急物流配送的目标是以较快的速度安全地将有限的物资送达需求地，是多目标问题。

1 模型的构建

1.1 模型的描述和符号说明

设有m个应急需求点集合，其在计划期内发生突发事故的概率为需求点j所要求的服务数量为Mj；n个备选的应急服务设施中心集合，其建设容量为从应急服务设施中心i到需求点j的应急时间为tij，由应急服务设施中心i到需求点j运送应急资源的单位运输费用为cij，应急服务设施中心i到需求点j应急资源的运输量为xij；需求点j一般要求的应急服务必须在时间ETj内到达；q为应急服务设施中心i所提供救援服务的需求点的数量；pjh为车辆在路径j,（）h 上的安全通过概率。已知应急服务中心i的开设费用为Si，灾害损失函数为dj（t），救援函数为时刻表示救援车辆到达需求点j的时间；为第c种物资每单位物资的重量；为第m种运输方式下，v种类型运输车辆的载重量；为第m种运输方式下，直接相邻的n1点，n2点关于v种类型运输车辆的道路容量；为t时段在第m种运输方式下，通过弧 （n1,n2）点n2接收到的c种物资的数量；为t时段在第m种运输方式下，经过弧 （n1,n2）到达点n2的v种类型运输车辆的数量。

1.2 建立多目标函数

本文应用免疫结合蚁群的混合算法对应急物流的配送路径进行安排。不仅从运输时间方面，更融入了安全通过概率和运输距离两个目标，对应急物流运输路线优化问题进行求解。

假设决策变量为：bjh=1，应急车辆经过；否则为0，应急车辆不经过。

（1） 时效性

设Ti为所有应急服务设施中心i到其提供救援服务的所有需求点的运输总时间，tjh为应急服务设施中心i的救援车辆在应急服务设施中心i所提供服务的需求点子类中的任意需求点j需求点h路径（j,h ）上的行驶时间 （1■j≠h■q ）。目标是对于应急服务设施中心i，其到所提供服务的所有需求点的运输时间为Ti，即，时效性的目标是让Ti最小。则对于应急服务设施中心i，基于时效属性的目标函数为：

（2） 安全性

pjh为车辆在路径上的安全通过概率，车辆安全通过有q个需求点的整条路L的概率为：即，

推动校企合作办学是此次课程考核评价改革的亮点之一。在实践环节的考核阶段，根据训方案的确定、实验操作和熟练程度等考核指标进行一一对照，尝试将学生和企业一线员工纳入考核评价团队，提高评价的客观性和公正性。

1

（3） 经济性

设Di为所有应急服务设施中心i到其所提供服务的q个需求点运输线路总距离，djh为车辆在任意路径j,（）h 上的行驶距离。

根据上述目标，可确定多目标函数如下：

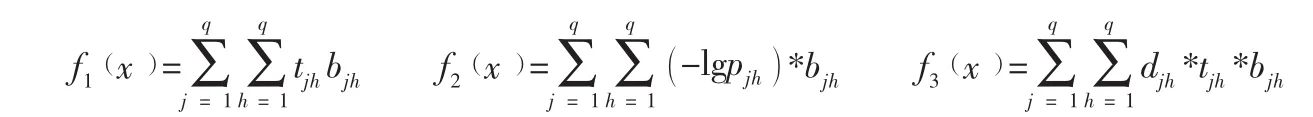
2 用免疫结合蚁群的混合算法求解

第一步，输入问题确认编码并设置启发信息[5]。

假设需求点j到需求点h所要花费时间是tjh，需求点j与需求点h之间的距离为djh，车辆通过路径j,（）h 的安全通过概率为lgpjh，则应急服务设施中心i对蚂蚁k的启发信息设置如下式所示。

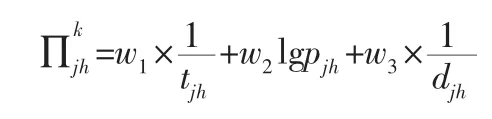
第二步，采用评价指标计算亲和力和排斥力。

考虑应急时间最早、通过路径的危险程度最小及运输距离最短三种优化目标时,蚂蚁k所取得的较优解与理想解的偏差ukr。寻找抗体和抗原的匹配程度，计算方法如下式。

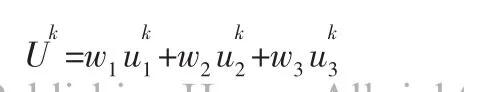
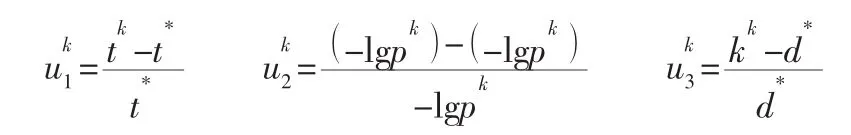
tk为蚂蚁k搜索到的最早应急时间，t*为在只考虑应急时间最早的情况下所取得的最早应急时间；-lgPk为蚂蚁k搜索到的通过路径的最小危险程度，-lgP*为在只考虑危险程度最小的情况下取得的最小危险程度；dk为蚂蚁k搜索到的最小运输距离，d*为在只考虑运输距离最短情况下取得的最小运输距离。

第三步，抗体选择，按照 “优胜略汰”的自然选择机制，在新产生的若干抗体中，选择与抗原匹配较好的抗体构成新的集合，转第二步。

第四步，更新信息素。

为更好地利用全局信息，同时避免算法陷入局部最优，本论文采用免疫算法，将各个物资供应点的信息素限定在之间。

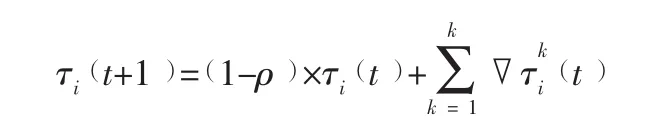
上式中，Q为常量，表示信素强度，它在一定程度上影响算法的收敛速度，共有K只蚂蚁，表示第k只蚂蚁在本次搜索中所得到的最小偏差值。τi（t）为t时刻节点i的信息素，为第k只蚂蚁在经搜索所得到的节点集合，ρ为信息素挥发因子。

应急资源运输路线安排方案调整考虑到灾害发生后各种随机因素的影响,车辆在途中应根据实时交通信息随时调整原始行驶路线。构造适当的免疫算子pi，处理获得的当前时段路段行程目标预测值,若计算得到的车辆最优路径比初始路线方案节省一定的程度 （如至少节省10%的行程目标值），那么新的行车路线可被接受，车辆按新路线行驶；否则，仍维持原路线不变。

第五步，进行迭代循环，知道满足算法的停止条件为止。

3 模型检验与分析

设 9个应急点为1,2,3,4,5,6,7,8,9。它们之间的距离表示如下：

4 结束语

本文综合考虑了应急救援物资调度在运输时效性、经济性和安全可靠性等要求，而不是把应急物资的调度的研究目的仅仅局限在运输成本最小或是应急时间最短；考虑多物资运输，多类型车辆，和道路受损引起车辆运行时间的随机性等因素；在求解模型时，运用人工免疫算法和蚁群算法的混合算法，快速求解实时应急求援物资运输问题，有效提高寻优精度和响应速度。并对其进行实证研究，通过不同算法的比较，验证本文模型和算法的可行性和有效性，为应急管理部门提供有效的辅助建议。

[1] Jae Young choi.Stochastic Scheduling Problems for Minimizing Tardy Jobs with Application to Emergency Vehicle Dispatchingon Unreliable Road Network[D].Unpublished Doctors Thesis,University of New York,2003:61-68.

[2] Gulay Barbarosoglu,Linet Ozdamar,Ahmet Cevik.An Interactive Approach for Hierarchical Analysis of Helicopter Logistics in Disaster Relief Operations[J].European Journal of Operational Research,2002,140(1):118-133.

[3] 卢安文.紧急情况下的物流配送模型[J].西南石油学院学报，2003,25(1):80-83.

[4] 陈雷雷，王海燕.大规模突发事件中基于满意度的应急物资优化调度模型[J].中国安全科学学报，2010(5):46-52.

[5] 马建华，房勇，袁杰.多车场多车型最快完成车辆路径问题的变异蚁群算法[J].系统工程理论与实践，2011,31(8):1508-1516.