多相异步电机电磁噪声研究

唐剑飞 王林

(中国舰船研究设计中心军事代表室，武汉 430064)

0 引言

相比普通三相电机，多相电机具有噪声小、能缺相运行等优点。但随着相数增多，电机的电磁场的有限元分析变得越发复杂。有限元法能较好地解决电磁场计算中的通用性与精确性的问题。通过设定电机的模型、材料属性、激励、初始状态等条件后，可以通过有限元方法计算出该电机任意时刻的运行参数，进而分析电机的噪声情况。由于所研究异步电机无通风道设计，使用二维（2D）有限元已经可以满足计算精度，故文中所涉及的异步电机的仿真是利用Ansoft软件[1]中的Maxwell 2D求解的。

1 空载条件下的电机电磁场分析

以某型双Y移30°六相电机为例，仿真时其外电路设置如图1所示。

通过处理稳定运行时电机电磁场，得到气隙磁密径向分量如图2所示。

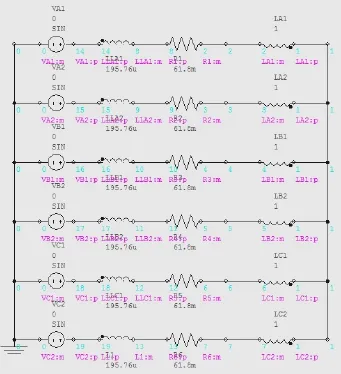
图1 外电路设置

通过仿真可以得到某型样机在绕成3相或6相，在不同短距比条件下空载气隙磁场的径向分量频谱，如图3至图6所示。

对比图3至图6可以看出，在定子结构相同，相数不同或节距不同时，谐波的主要成分相同。在三相电机的气隙磁密中含有明显的 5、7次等6k±1次谐波，而六相电机的气隙磁密中则含有明显的11与13次等12k±1次谐波。当短距比不同时，电机对应谐波的幅值不同。在所给出的四种短距比中，短距比为5/6对应的三相电机的5、7次谐波幅值最小，而短距比为 11/12对应的六相电机气隙磁场中的11与13次谐波幅值最小。通过对气隙磁场进行计算[2]，可以得到样机在不同条件下气隙磁密频谱与定子铁芯所受径向力频谱，见图7、图8。对比图7与图8可以看出，在定、转子槽数采用近槽设计后气隙电磁场以及径向力波的构成无明显变化。

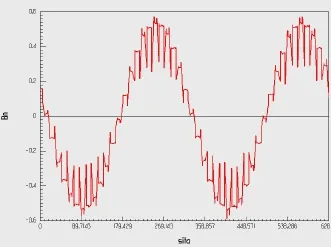
图2 气隙磁密的径向分量

图3 短距比为3/4时磁密频谱（a为三相，b为六相）

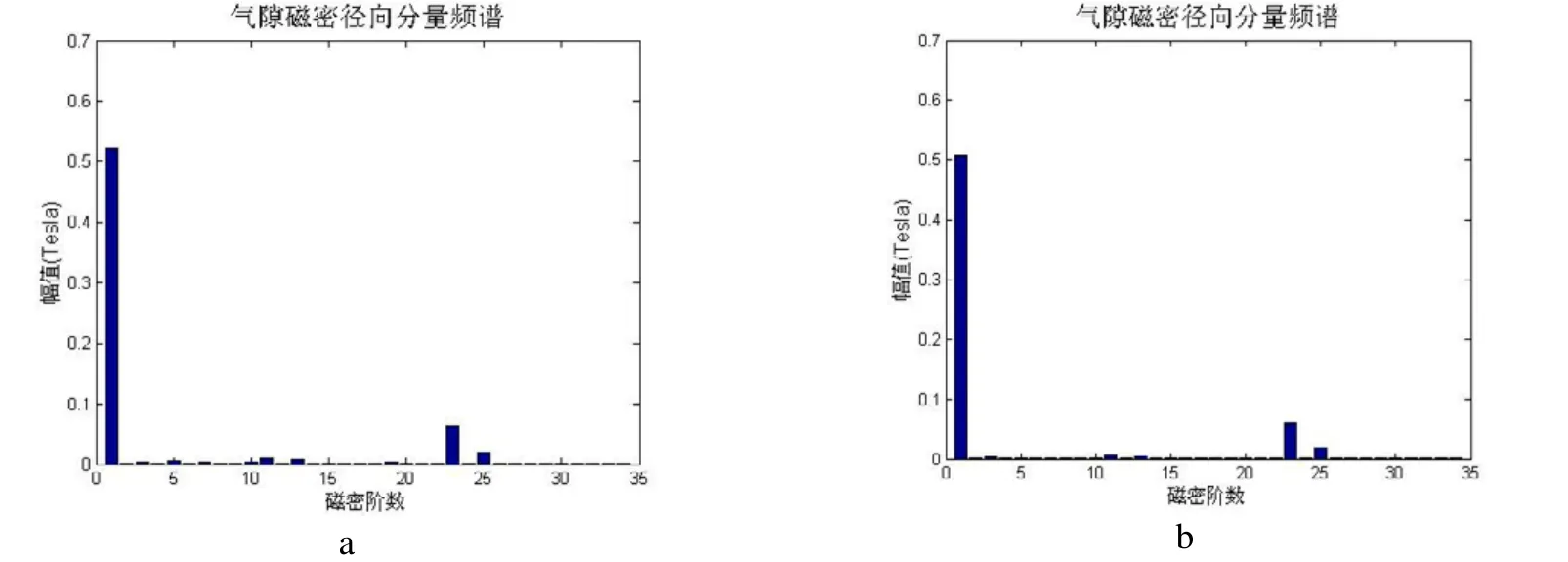
图4 短距比为5/6时磁密频谱（a为三相，b为六相）

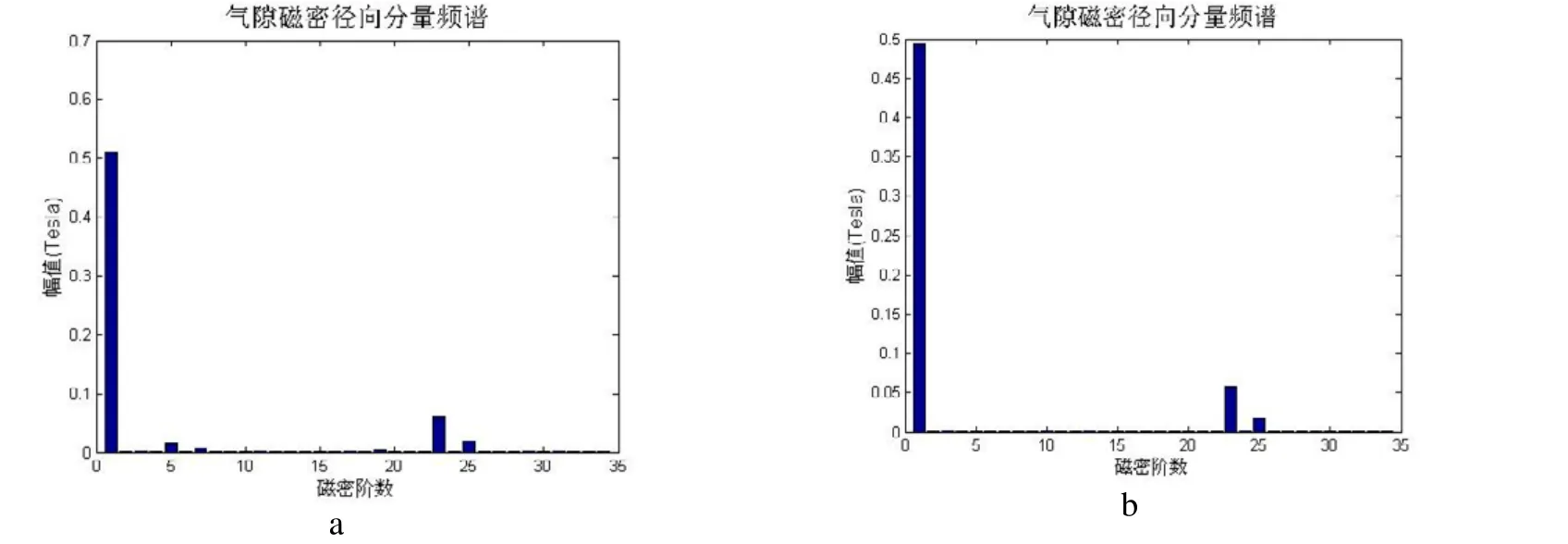
图5 短距比为11/12时磁密频谱（a为三相，b为六相）

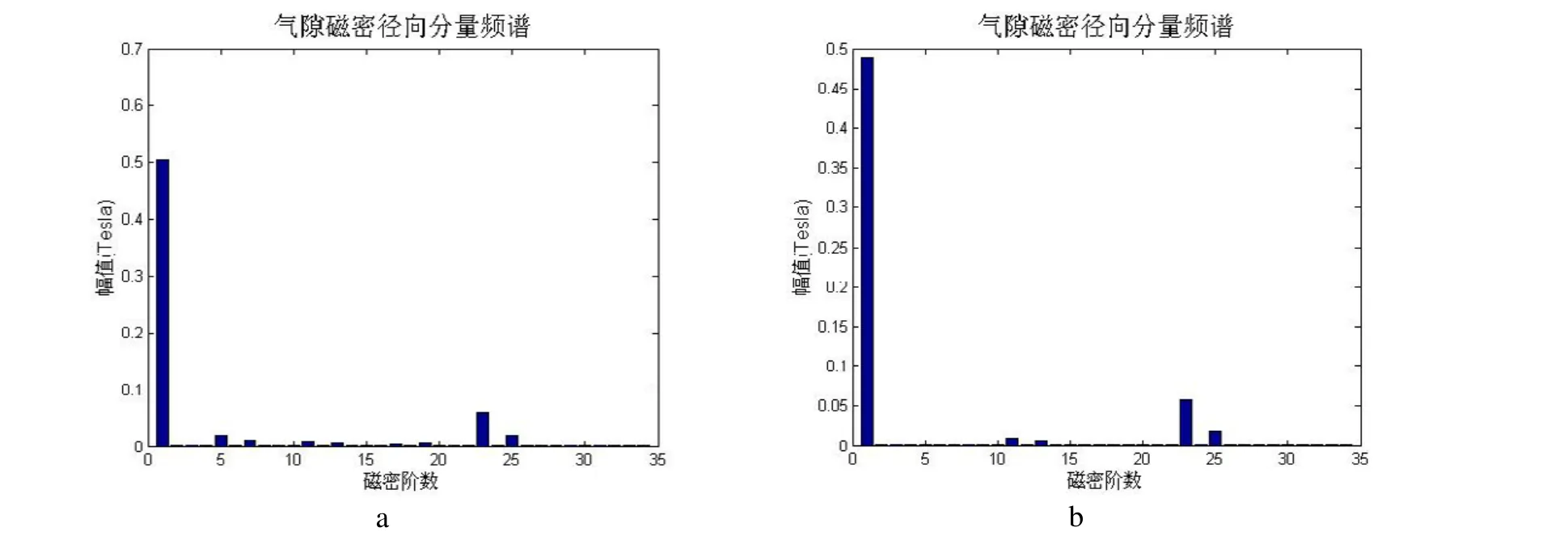
图6 短距比为1时磁密频谱（a为三相，b为六相）

图7 转子槽数为45时气隙磁密频谱与定子铁芯所受径向力频谱

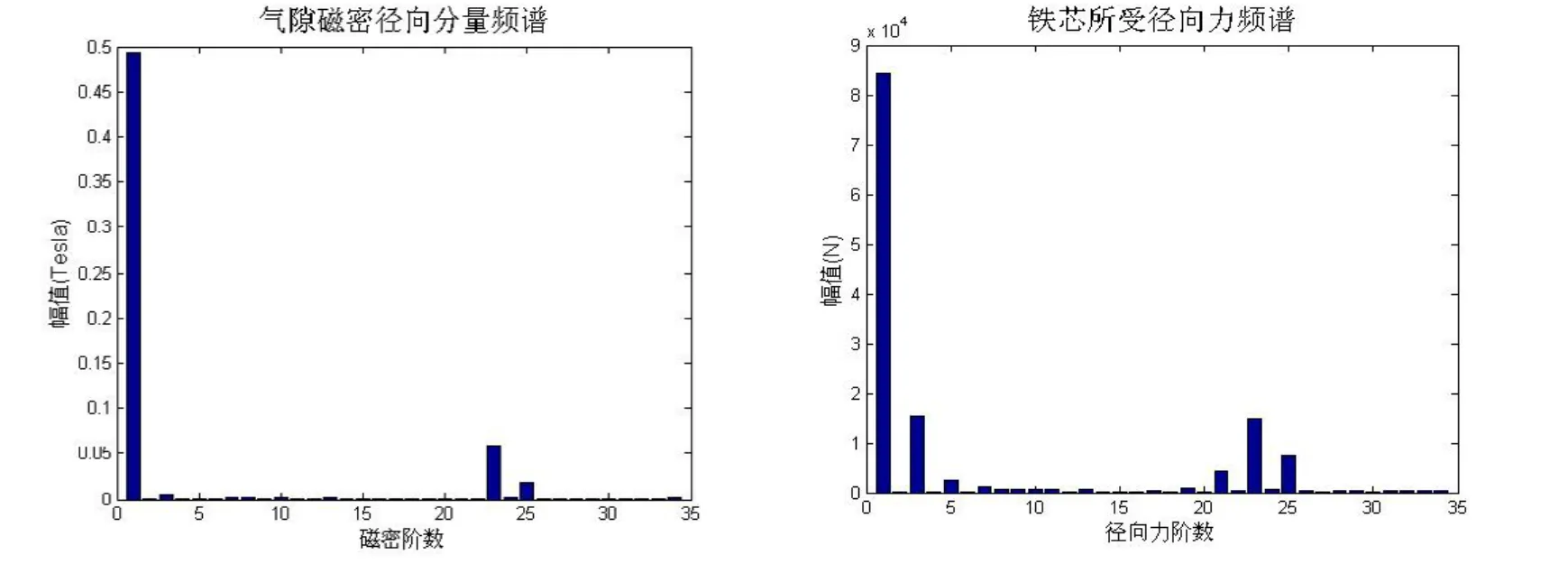
图8 转子槽数为47时气隙磁密频谱与定子铁芯所受径向力频谱

所受径向力频谱，在对不同条件下频谱图进行分析后可以得到与磁场分析大体相同的结论。因此，从减小谐波含量以减小电机噪声的角度考虑，当电机绕成三相时，短距比应取为 5/6，而电机绕成六相时，短距比应取为11/12。

利用相同方法得到定子绕组绕成六相、转子槽数为 45和47、短距比为 11/12时气隙磁密径向分量频谱与定子铁芯所受径向力及对应频谱如图7与图8。

2 负载对电机定子铁心所受力波的影响

当异步电机由空载过度到负载运行时，转子转速变化不大，但随着负载的变化，转子电流会发生较大变化，从而引起气隙磁场变化[3]，最后导致电机噪声相与空载时存在较大差别。另一方面，转子电流增加会使作用在定子上的作用力变大，导致定子振动位移加大，进而增加电机噪声[4]。图9为样机绕制成六相、短距比为 5/6时，不同的负载转矩条件下通过Ansoft分析得到的电机定子铁芯所受径向力频谱。其中 a、b、c、d分别对应负载转矩为0 N·m（空载）、20 N·m、40 N·m与54.2 N·m（满载）条件下的仿真结果。

图9 不同负载条件下定子铁心所受径向力频谱

通过对比可以看出，随着负载的增加，电机铁心受到的各次径向力幅值出现了不同程度的增长，因此负载条件下，电机所发出的电磁噪声将会高于空载下的噪声值。正常工作的电动机都是带载运行的，有必要研究电机的负载噪声抑制方法。

3 结束语

本文利用 Asoft软件，对不同短距系数与不同转子槽数条件下的空载及负载时的电机运行情况进行了仿真。利用仿真得到的电磁场数据计算了不同条件下气隙磁密径向分量频谱与定子所受径向力频谱，并对各频谱的构成进行了分析。

对比得出了为减小气隙磁场的谐波含量，三相电机的短距比应选择 5/6，而六相电机的短距比应选择 11/12的结论。根据电磁场数据计算出了不同条件下气隙磁场的径向分量频谱与定子所受径向力频谱，并对各频谱的构成进行了分析。通过分析空载与不同负载条件下的电机磁场数据，得出了负载会增加气隙磁场径向分量及定子铁芯所受电磁力中所含的谐波的幅值，进而会增加电机噪声。

[1]刘国强, 赵凌志, 蒋继娅. Ansoft工程电磁场有限元分析[M]. 北京, 电子工业出版社, 2005: 92-97.

[2]陈永校, 诸自强, 应善成. 电机噪声的分析和控制[J]. 山东科技大学学报, 2000, 19(3): 80-82.

[3]王益红. 异步电动机的负载噪声分析[J]. 山东科技大学学报, 2000, 19(3)：80-82.

[4]祝长生, 陈永校. 变频器供电的三相异步电机的噪声特性[J]. 中小型电机, 1997, 24(5): 9-12.