线性神经网络在舰船磁场推算模型中的应用
范世武
(海军北海舰队司令部装备处,山东青岛 266000)
0 引言
近年来,闭环消磁技术成为各国消磁研究热点,相较于目前的消磁系统控制方法,它可以实现固定磁场的实时补偿,是未来磁隐身技术发展的必然趋势。为了获取较多的舰船内部信息,传感器应该与船壳非常接近,测量所得的磁场是舰艇内部复杂的近场值。相对于目前较成熟的磁场深度推算问题,内外磁场推算属于不同的半空间,且存在磁屏蔽现象,很多深度换算中的成功模型(如:磁偶极子等)难以直接应用[1]。因此,寻找一种根据舰船内部磁场测量值能有效推算舰船外部某特定深度上磁场的方法成为实现闭环消磁技术的关键,也是闭环消磁技术亟待解决的问题。
本文从智能优化的角度出发,建立了内外磁场之间的线性神经网络(Linear neural network)预报模型。该方法避免了利用数值建模技术存在的诸多困难,即可实现舰艇内外磁场的换算,相较于其他数值建模方法其换算精度有所提高,并利用船模实验验证了所得网络的有效性和良好的泛化能力。
1 舰船磁场内外换算的数值建模技术
文献[2]中提到的校准矢量法具有原理简单、换算方便(不必网格剖分,不涉及复杂重积分计算)等优点,本文选取校准矢量法作为线性化建模的代表。该方法从虚拟磁源的理论出发,认为舰艇内外磁场均是由磁源产生的,如图1所示为内外磁场换算示意图。

图1 舰船磁场内外换算示意图
当磁场大小发生改变时,代表磁源的大小或方向发生改变,而内外传感器的位置相对于磁源位置是相对固定的,用矩阵表示如方程1所示:
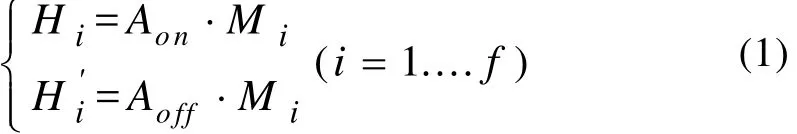
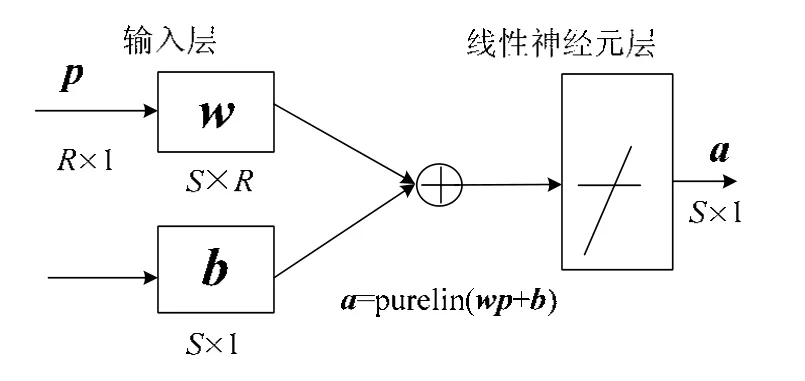
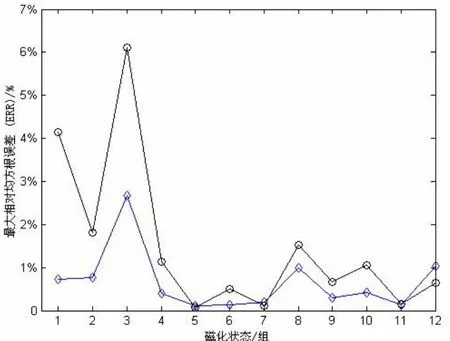
其中,iM代表磁源在第i种磁化状态下的磁矩列向量,iH、'iH分别代表舰船内、外部磁场强度值组成的列向量,onA、offA分别代表联系磁矩列向量与磁场强度的线性观测矩阵,矩阵中的每个元素由内外传感器布设位置与磁源布设位置决定。选取一部分磁化状态下的jH与j=1....m ,1 综上所述为目前国内外学者针对内外换算问题提出的较先进的线性建模方法,其误差主要来源于测量误差以及反演校准矢量SF时方程不定式造成的误差。与其它网络相比,线性神经网络[5-6]只能学习样本之间的线性关系,但其用于线性模型的预测时,具有收敛速度快、可达到零误差或很小的误差、误差曲线不存在局部极小点和平台问题的优点。本文讨论的内外磁场之间显然是一种线性关系,因此,选用结构最简单的线性神经网络来建立其线性关系。 线性神经网络可以由一个或者多个线性神经元组成。它采用Widrow-Hoff 学习规则即LMS(Least Mean Square)算法,主要用于函数逼近、信号处理滤波、预测、模式识别和控制等方面[1,4]。图2所示为一经典线性神经网络结构图,神经元传递函数为purelin;权值矩阵为w;阈值矩阵为b。利用舰船内外磁场分别作为输入、输出样本集对其进行训练,同时对网络的连接权值和阈值进行学习和调整,使网络有效辨识二者之间的线性关系。其中网络的重要参数,如输入向量维数R、隐层神经元数S、由内部磁场测量值以及补偿电流的维数确定。值得指出的是,不同于其它网络结构,如果输入与期望输出已知,线性神经网络可以直接设计,应用newlind()可以设计出特定的神经网络,其权值矩阵和阈值矩阵能够保证均方差最小。 图2 线性神经网络结构图 选取一两端封闭的空心圆筒作为潜艇模型(长2002 mm,厚6 mm),选用一可以自由推入推出圆筒的测量架,以便布设内部磁传感器,如图3所示。将7个传感器等间距布设在测量架中心线位置,将其推入空心圆筒内部,用以测量潜艇模型内部磁场,并在模型正下方0.594 m处,等间距布设7个传感器用以测量潜艇外部磁场,磁传感器具体布设如图4所示。 通过改变敷设在船模外部导线中的电流来模拟模型固定磁化状态的变化。在得到12组不同磁化状态下模型的内外测量数据后,任意选取其中11组内外测量数据作为A组,剩余1组内外测量数据作为B组。则BP神经网络的基本参数选取规则如下: 训练样本集:选取A组中的内部测量数据即文献[3]中的内部校准矢量jH作为训练网络的学习样本,A组中的外部测量数据即文献[3]中的外部校准矢量作为训练网络的期望输出; 测试样本集:选取B组中的内部测量数据即文献[3]中的Hk作为测试网络训练效果的输入样本,B组中的外部测量数据即文献[3]中的作为网络的理想输出,神经元个数:7。 图3 潜艇磁场内外换算的实物模型 图4 传感器布设示意图 图5 不同方法建模时,ERR比较图 本文从智能优化的角度出发,建立了内外磁场之间的线性神经网络预报模型,并通过船模实验验证了网络预测的准确性,相较于线性方法,换算精度有所提高,且有较高的稳定性,符合工程实际需求。 [1]X. Brunotte and G. Meunier. Line element for efficient computation of the magnetic field created by thin iron plates. IEEE Transaction on Magnetic, vol.26, 1990, pp. 2196-2198. [2]O. Chadebec, J.L. Coulomb, J.P. Bongirand, G.Cauffet and P.L.Thiec. Recent improvements for solving inverse magneto-static problem applied to shin shells. IEEE Transaction on Magnetic, vol. 38, 2002,pp. 1005-1008. [3]R M. Mack, R.A. Wingo. Ship degaussing system and algorithm. US Patent 6965505 B1 Nov.15,2005. [4]A. Salem and K. Ushijima. “Automatic detection of UXO from airborne magnetic data using a neural network”,Subsurface sensing technologies and applications, vol.2, no.3, 2001, pp. 191-213. [5]L.T. Lian, C.H. Xiao, S.D. Liu, G.H. Zhou and M.M.Yang. Magnetic field extrapolation based on improved back propagation neural network[C].Artificial intelligence and computational intelligence. Sanya,China: 2010, pp. 64-67. [6]吴莉莉, 曹晴, 李辉. ICA 和线性神经网络在带噪语音分离中的研究[J]. 计算机工程与应用, 2010,46(16): 143-146.
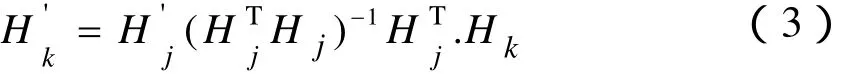
2 线性神经网络模型基本原理
3 潜艇内外换算神经网络预报模型的有效性验证
3.1 基于线性神经网络的潜艇磁场内外换算实验设计
3.2 线性网络基本参数的确定


3.3 网络训练以及网络评价
4 结语

