单相电力变压器高频传输特性研究

张元峰 孟进 张向明 赵治华

（海军工程大学电力电子技术研究所，武汉430033）

0 引言

大容量的电机驱动系统前端能量接口多为整流变压器，其主要功能是将电站高压电网降压成变频器所需的电压等级，同时合理的变压器方案可以有效地提高电网波形质量和运行功率因素。然而，这些基于 PWM技术的变频驱动装置在工作时会产生强的传导电磁干扰，这些干扰电流会通过变压器向电网或其它装置进行传播。因此，在研究包含变压器元件的电力系统的电磁干扰传播规律时，必须建立包括变压器高频模型的数学模型。

目前关于功率变流器传导电磁干扰传输特性的研究[1]，主要针对变流器本身电磁干扰的产生和传播机理进行研究，所得到的干扰传播途径没有包含变流器前端常用的配电变压器，因而不能真实反映干扰在电网接口的传播与耦合特性。要准确地描述变压器的高频传输特性，从电路上讲就是需要得到由电阻、电感和电容组成的电路网络。传统的电力电子分析考虑的是低频（50/60 Hz）的功率信号，建立的数学模型常常忽略高频寄生参数。实际测试结果表明，在高频下，变压器的电路特性主要取决于寄生分布参数，具体讲就是变压器漏感、绕组电阻和分布电容。文献[2]在研究含有变压器的PWM软开关变换器时，将变压器的高频模型用漏感和匝比来描述，没有考虑寄生电容对电压和电流波形的影响。文献[3]考虑了变压器绕组之间的容性耦合，建立了包含寄生电容在内的变压器模型，但是计算量大，不适合快速计算和分析。

基于传统的变压器三电容等效电路，考虑不同频段下寄生参数对变压器传输特性的影响，将变压器电路简化为只含主要寄生参数的谐振电路，导出谐振频率，用谐振频率法求取变压器寄生电容。依据二端口网络理论导出变压器原副边电流传输函数及空载电压传输函数，利用Matlab软件对高频传输特性进行了计算，最后通过实验结果验证了所提出的模型的正确性。

1 变压器三电容等效电路模型

建立能够准确描述变压器高频传输特性的电路模型有较好的工程应用价值。

研究表明[4]，在满足以下两个条件下，图1所示的三电容集总等效电路具有足够的精度。

1）原边和副边作为两个输入端，分别记为A，B和C，D。变压器始终为一个四端子网络，因此在整个测量过程中，只改变A、B、C和D四个端子的接线方式，变压器联接组、铁芯、屏蔽层等结构保持不变。

2）忽略导线及铁芯涡流损耗。

图1中，若将 CD看作次级，则次级的绕组电阻及寄生电容已折算到原边。rw1和 rw2分别为原边和副边绕组电阻，LSC为漏感，Lm为激磁电感，R0为激磁电阻，C1和 C2分别为原边和副边绕组自电容，C12为绕组互电容。虚线框表示理想变压器，η为理想变压器的电压比。

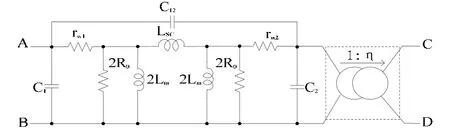
图1 变压器三电容集总等效电路

2 变压器高频信号的传输方程

对图 1所示等效电路进行变换，可得到图2所示的二端口网络模型，其中，用Zeq来等效理想变压器的输入阻抗。

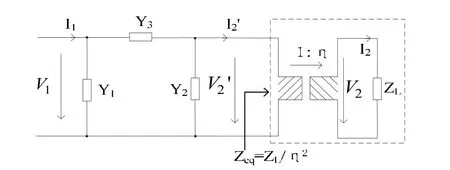
图2 变压器等效电路模型的变换

图2中,导纳 Y1～Y3表达式如下：

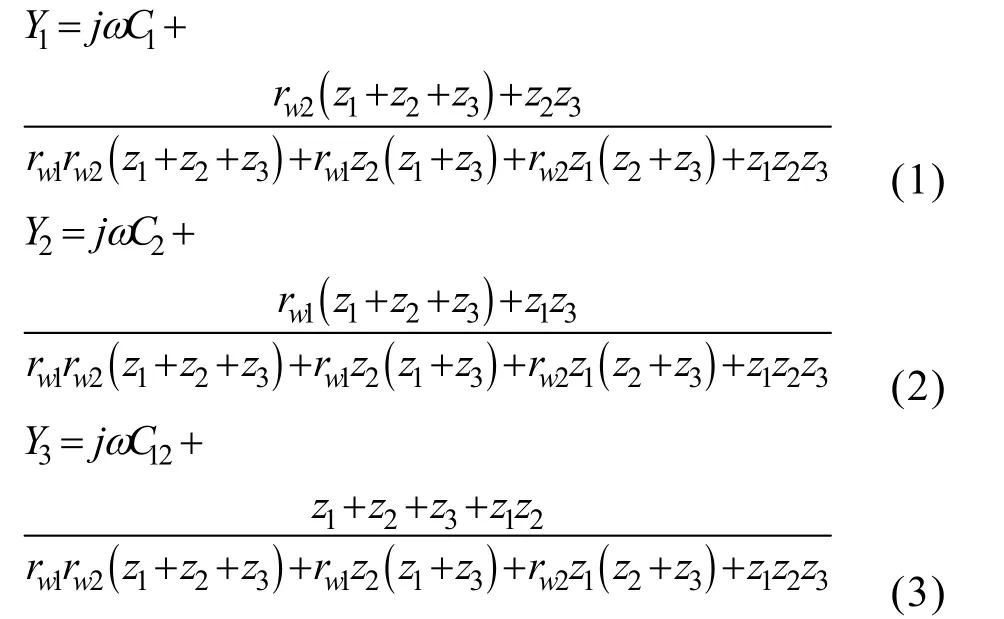
式中，

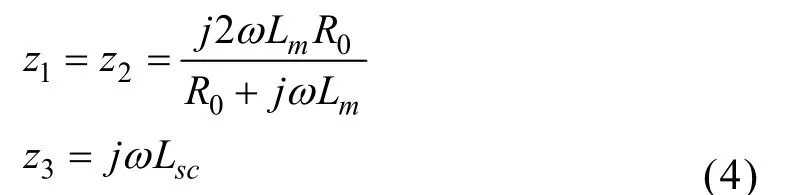
图2折算到原边的π型电路二端口T参数方程：

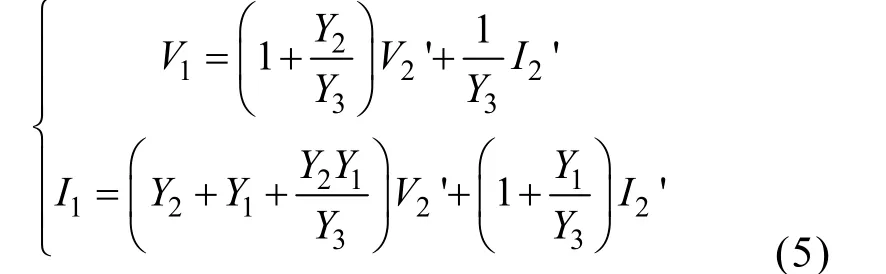
虚线框理想变压器二端口T参数矩阵：

从而得到，带载时变压器副边电流与原边电流的比值关系：

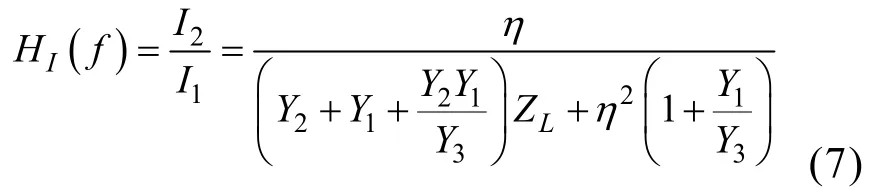
空载时，变压器输出电压与输入电压的比值关系为：

当分析包含变压器的电力系统网络时，若得到变压器负载（电力电子变流设备）端口的干扰电压或干扰电流，就很容易求出电网接口处的干扰电压和电流。

3 变压器高频模型参数提取方法

3.1 磁性耦合参数Lm，Lsc及η的实验提取方法

磁性耦合部分的参数主要指漏感及激磁电感。将从原边看进去的开路阻抗及短路阻抗的虚部对应的电感分量分别记为L0和Ls，从副边看进去的开路阻抗的虚部对应的电感分量记为L0'，则对较强耦合的变压器而言，Lm和LSC分别与 L0和 Ls相等，且 η2=L0'/ L0。通过观察短路阻抗的串联电感分量可确定漏感的值。

3.2 绕组电阻rw1和rw2及磁芯损耗电阻R0的实验提取方法

在低频下，从某一边看进去的开路阻抗的模近似为一常数，该常数即为该边的绕组电阻，如果该常数的截止频率低于设备的测量频率，则可以通过直接测量阻抗的电阻分量读出绕组的阻值。开路阻抗第一个谐振频率处的阻抗模值即为磁芯损耗电阻值。

3.3 基于谐振频率法提取寄生电容

由图 2可知，在每个频率点处，二端口网络模型可由三个独立阻抗参数来确定。在实际测量中，可以直接得到变压器的四个阻抗参数，即副边开路时，原边输入阻抗Z0；副边短路时，原边输入阻抗ZS；原边开路时，副边输入阻抗Z0'；原边短路时，副边输入阻抗ZS'。只需选择三个阻抗的测试值进行分析，就可以得到三个寄生电容的数值。

图3 阻抗模值和相角渐进线

图3为变压器四个阻抗的幅值和相角渐进线图，粗实线表示Z0的相位曲线。f1和f2分别为 Z0的第一个并联谐振频率和串联谐振频率,f3为ZS的第一个并联谐振频率。若不考虑等效电路中的电阻，可分别求解出f1、f2、f3的计算公式：

根据上述主导谐振点的频率计算公式及实际测量得到的阻抗曲线谐振频率，就可提取图1所示变压器三电容等效电路模型中三个电容参数。

4 实验验证

测试用变压器的铭牌参数：容量500 VA，电压比：12 V/220 V，频率：50－60 Hz。测量仪器为Agilent4294A精确阻抗分析仪，扫频范围40 Hz～50 MHz。首先，测量得到的Z0和的串联电阻和电感曲线电感低频值分别为4.95 mH和1602.9 mH，则激磁电感Lm=4.95 mH，推算变比与标定电压比18.33很接近。rw1=0.134 Ω，η2rw2=41.16 Ω，R0=237.48 Ω，则 rw2=0.124 Ω；其次，通过测量Zs串联电阻和电感测量曲线，得到漏感值LSC=16.79 µH；最后，根据从原边看进去的开路阻抗及短路阻抗曲线及前面求取的主导谐振频率公式，计算得到C1、C2、C12如表1所示。

表1 寄生电容C1、C2、C12的求解结果

从结果看到，C1为负电容。负集总电容表面上是减小了总的静电能量[5]，为满足由集总耦合电容参数表示的静电能量与由分布电容描述的静电能量相等这一前提条件，在电路仿真软件中（例如MATLAB等）能够处理包含负电容的电路。

为验证以上分析及模型的正确性，对实际变压器宽频带范围内的传输特性进行测量，测量仪器为 NF5096频率特性分析仪（附带 1 Ω精密电阻）。变压器作为一个二端口，将信号源接到变压器输入端，负载电压信号及1 Ω精密电阻上的电压信号分别接到分析仪的两个通道，传输特性计算公式分别如式（12）（13）所示：

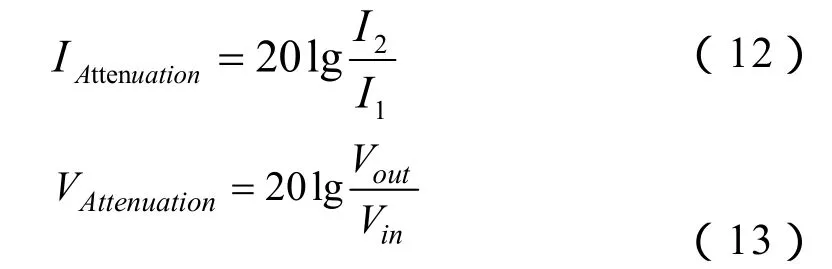
根据参数提取结果，变压器模型参数如下：rw1=0.134 Ω，rw2=0.124 Ω，LSC=16.79 µH，Lm=4.95 mH， η=18.22， R0=237.48 Ω ，C1=-5.7665 nF， C2=65.9960 nF，C12=5.8045 nF，ZL=10 Ω。利用MATLAB软件，分别得到式（12）（13）对应的原副边电流传输特性及空载时原副边电压传输特性计算结果，与测量值的比较如图4和图5。

图4 电流传输特性计算值和测量值比较

图5 电压传输特性计算值和测量值比较

图4及图5表明，在50 Hz～500 kHz频段，计算值与测量值吻合得较好，该频段内的最大误差为0.1 dB。另外，比较宽频段范围内的计算值和测量值看出，在不同的频率段，信号具有不同的传输特性。在50 Hz～10 kHz较低频段，原副边传输信号的传输比例不变；在 100 kHz～1 MHz左右，信号急剧衰减，而在1 MHz以上频段，电流比呈现被放大趋势。这一方面表明变压器高频信号传输特性的复杂性，另一方面表明有必要分频段建立包含低频参数和高频参数的变压器网络模型，研究分布电容等参数对变压器高频信号传输规律的影响。

5 结论

本文对变压器高频信号传输特性进行研究，考虑了变压器高频下不可忽略的寄生参数影响，基于变压器三电容缩减模型，用谐振频率法求取变压器寄生电容，并提出了谐振频率公式的计算模型。计算与直接测量结果表明，在50 Hz～500 kHz频率段，缩减后得到的三电容等效电路模型能很好的描述变压器高频信号传输特性。

比较宽频段范围内的计算值和测量值看出，在不同的频率段，信号具有不同的传输特性，为下一步分频段建立包含低频参数和高频参数的变压器网络模型，研究分布电容及η等参数对变压器高频信号传输规律的影响提供了参考。本文对进一步研究分布参数对高频信号的传输作用规律及实现EMI抑制的最优效果具有一定指导意义。

[1]钱照明, 陈恒林. 电力电子装置电磁兼容研究最新进展[J]. 电工技术学报, 2007, 22(7)： 1-11.

[2]Claudio Y. Inaba, et al. High frequency transformer - assisted passive soft switching PWM DC-DC converter with energy recovery for compact Auxiliary power supply in rolling stock transportation[C]. IEEE IAS, Salt Lake City, Utah,USA, 2003.

[3]Hai Yan Lu , Jian Guo Zhu, et al. Experimental determination of stray capacitances in high frequency transformers[J]. IEEE Trans. on Power Electronics, 18(5), 2003：1105-1112.

[4]Cogitore B, Keradec J.-P. The two-winding transformer： an experimental method to obtain a wide frequency range equivalent circuit[J]. IEEE Trans. on Instrumentation and Measurement,43(2). 1994： 364-371.

[5]Blache F, Keradec J.-P. Stray capacitances of two winding transformer： equivalent circuit, measurements, calculation and lowering[C]. IEEE IAS Conf. Rec., 1994： 1211-1217.