基于Matlab的轮式悬架移动平台动力学建模与仿真

张建华，刘宇鹏，张明路

（河北工业大学 机械工程学院，天津 300130）

0 引言

随着科技的发展，移动机器人已普遍应用于工业、农业、军事侦察、空间探索等领域，其中，移动机器人的行进方式仍然以轮式应用最为广泛[1]。通常情况下，多数轮式移动机器人没有安装悬架系统或安装悬架系统后模型中未考虑其对整体机构影响，而只考虑执行机构，将移动载体的自由度加到执行机构上，使其变为冗余机构，单独对轮式悬架移动载体进行研究较少[2]。对于非结构环境下的轮式悬架移动平台而言，悬架的运动学以及动力学分析是轮式悬架移动平台设计、运动校核的重要内容之一[3]。悬架的重要评价指标[4,5]有悬架的动挠度、轮胎的动载荷和车身加速度，这些参数对悬架的设计起到重要作用[6,7]。此外，车身俯仰角及侧倾角的变化规律关系到车体的控制策略。

本文针对轮式悬架移动平台，对非结构路面情况进行了分析并建立模型[8]，之后对轮式悬架移动平台悬架系统的动挠度、轮胎动载荷、车身垂向加速度、车身俯仰角及车身侧倾角等重要指标参数建立数学模型，进行模拟仿真。

1 路面激励模型

由于轮式悬架移动平台所处工作环境路面情况未知，即非结构环境，为此必须建立一个合适的路面激励模型。在对线性悬架系统进行动力学分析研究时，通常要在时域里进行。产生随机路面不平度时间轮廓通常有两种方法，即由一白噪声通过积分器产生或由一白噪声通过成形滤波器产生，本文将采用第一种方法生成路面输入：

路面功率谱密度函数表达式如下：

将其转化为时间频率下路面不平度垂直速度功率谱密度：

当车速u为定值时，密度谱为常数。故路面轮廓即可由谱密度为白噪声加随机数通过积分器产生，表达式为：

当移动平台速度u=1.2m/s,路面为C级时：

图1 路面Simulink模型

根据以上分析，在Matlab/Simulink中建立仿真路面模型，如图1所示，左（A、C轮）右（B、D轮）两侧车轮采用不同路面输入。

2 轮式悬架移动平台建模与仿真

2.1 轮式悬架移动平台建模

2.1.1 轮式移动平台整车模型

本文忽略轮式悬架移动平台所承载的执行机构，建立的轮式悬架移动平台物理模型如图2所示。

图3为七自由度整车振动模型图，该模型主要考虑车体垂直、俯仰、侧倾3个自由度以及4个车轮质量的4个垂直自由度，共7自由度。

图2 轮式悬架移动平台物理模型简图

图3 轮式悬架移动平台七自由度整车模型

其中A、C分别为左前、左后轮；B、D分别为右前、右后轮；mb为车身质量；Ip为车体俯仰转动惯量；Ir为车体侧倾转动惯量；m1为车轮质量；k2为悬架刚度；c2为悬架阻尼系数；k1为轮胎刚度；a、b为前后轮距质心的距离；tf、tr为汽车左右轮到质心的垂直距离；xb为车身质心的垂向位移；θ为车身的俯仰角；φ为车身的侧倾角。

根据车体的受力情况建立如下车体运动微分方程。

车身质心处的垂向运动微分方程：

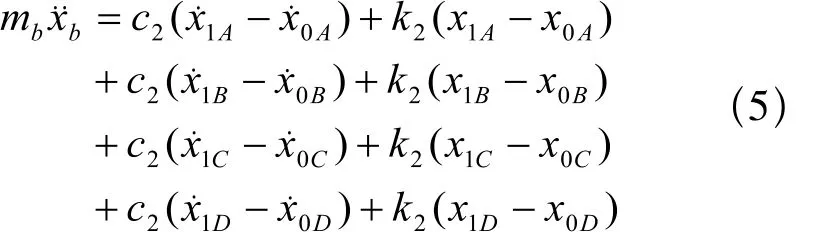
车身俯仰运动微分方程：

车身侧倾运动微分方程：

四个车轮的运动微分方程：

根据方程(5)～(11)在Matlab/Simulink中建立整车仿真模型如图4，仿真参数如下：

mb=48kg；m1=1kg；k1=8937N/m；k2=4115N/m；c2=412N/m；a=0.26m；b=0.27m；tf=0.21m；tr=0.21m；Ip=3.372kg·m2；Ir=2.117kg·m2。

图4中，xb表示车体质心垂向位移，Theta表示车体俯仰角，Fi表示车体侧倾角（前面加字母D表示对其微分）。其中路面子系统为路面激励模型，左（A、C）右（B、D）两侧轮子采用不同的随机路面激励；反馈子系统表示了三个输出变量xb、Theta、Fi的反馈信号；函数模块编辑函数与输入输出变量间的数学关系；时钟模块为了把时间t导入到Matlab的workspace中方便后续绘图工作，设置Simulink仿真时间为10s。

2.1.2 四分之一车悬架模型

为了研究轮式悬架移动平台的悬架动挠度、轮胎动载荷等悬架关键量化指标对移动平台的影响，在随机路面激励下，对于四组不同的悬架参数的时域变化趋势进行简要分析，从而选取适合移动平台的悬架系统的刚度、阻尼系数。

建立四分之一车体被动悬架模型，如图5所示（由于轮胎阻尼系数影响相对较小，故忽略不计）。

图5 四分之一车模型

m2为四分之一车体质量，m1为轮胎质量，k2、c2分别为悬架刚度和阻尼系数，k1为简化轮胎刚度，x0为路面随机激励，x1，x2分别为轮胎和车体的垂向位移。

根据牛顿第二定律以及相关的振动理论，列出线性被动悬架移动载体车身与车轮两自由度车辆振动模型的振动微分方程：

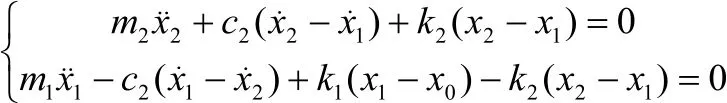
其输入为路面随机信号，输出为悬架动挠度x2-x1和轮胎动载荷k1(x1-x0)。

在轮胎刚度不变的情况下选取的四组悬架刚度阻尼值实验参数，如表1所示。

表1 刚度阻尼样本

其他参数m1=1kg；mb=48kg（车身总质量）。

2.2 仿真结果及分析

2.2.1 整车仿真结果分析

车身质心在C、D级路面状况下的垂向加速度时域仿真曲线，如图6所示，随着时间的增加，车身垂向质心加速度在C级路面上变化范围大概在-0.1m/s2～0.3m/s2之间（D级路面在-0.2m/s2～0.5m/s2之间），C级路面7秒（D级在5秒8秒）左右，仿真曲线发生一次突变，分析认为该突变是由于地面随机输入信号在某些时刻变化过大而造成。总体来说波动较为平稳，速度变化量不大，车体较为稳定。

车身俯仰角在C、D级路面状况下的时域仿真曲线如图7所示，随着时间的变化车身俯仰角在C级路面-0.1rad～0.15rad之间（D级路面在-0.25rad～0.35rad之间）波动变化、变化角度相对比较小，且基本围绕着0上下轻微浮动，这样保证了移动平台不会剧烈俯仰，在可控范围之内。

图6 车身垂向质心加速度

车身侧倾角在C、D级路面状况下的时域仿真曲线如图8所示，随着时间的变化车身侧倾角变化范围在C级路面-0.01rad～0.1rad之间（D级路面在-0.02rad～0.23rad之间）波动变化，基本角度变化范围不大，围绕着0轻微浮动，这样保证了移动平台不会剧烈侧倾，仍在可控范围之内。

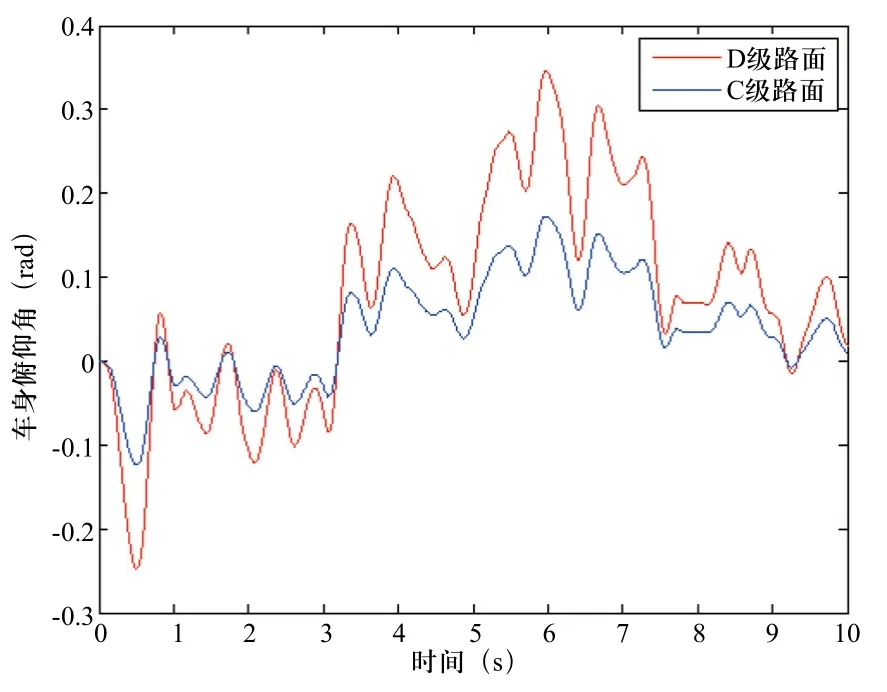
图7 车身俯仰角

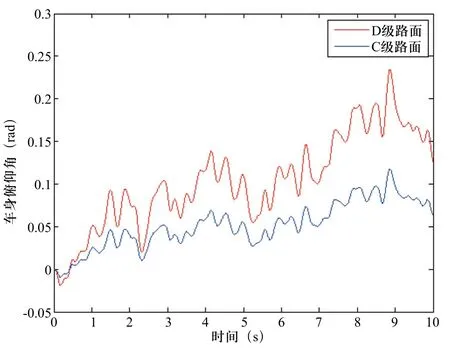
图8 车身侧倾角

路面等级由C至D（即由好变坏），这三个输出变量波动变大，与实际情况相符。仿真结果印证了悬架系统对轮式移动载体在非结构环境下平稳行驶有很大的作用，为轮式悬架移动载体的控制器设计奠定了基础。

2.2.2 四分之一车仿真结果分析

以下为悬架动挠度（图9 (a)-(d)）、及轮胎动载荷（图10 (a)-(d)）的时域仿真曲线。

不同刚度、阻尼系数下的悬架动挠度时域仿真曲线，如图9所示，随着时间和悬架刚度、阻尼系数的变大，悬架动挠度时域仿真曲线波动幅度由-0.06m～0.04m之间到-0.045m～0.04m之间，当轮式悬架移动平台行驶在不平路面时，可根据实际需要选择合适的刚度阻尼，以满足有足够动挠度来保障悬架不被“击穿”。

不同刚度、阻尼系数下的轮胎动载荷时域仿真曲线，如图10所示，随着时间和悬架刚度、阻尼系数的变大，轮胎动载荷时域仿真曲线波动幅度由-140N～120N之间到-230N～200N之间，轮胎动载荷略有增大，当轮式悬架移动平台行驶在不平路面时，若需要轮胎产生横向力时会对轮胎附着力产生影响，故对轮胎的选择又提出了挑战。

图9 悬架动挠度

3 结论

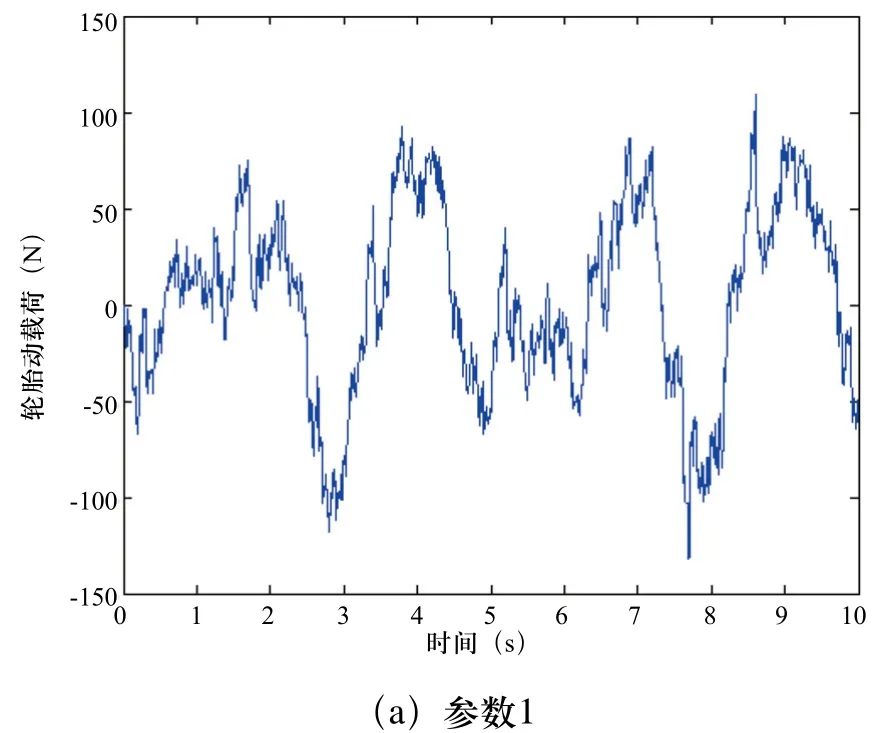
图10 轮胎动载荷

1）利用Matlab/Simulink对轮式悬架移动平台进行动力学仿真，能够通过其运动微分方程，很方便地建立计算机动态仿真模型，而且易于修改，省去了繁琐的程序编制，可以对车身垂直加速度、悬架动挠度、轮胎动载荷、俯仰角及侧倾角等变量进行跟踪。

2）仿真结果为轮式悬架移动平台在非结构环境下选择合适的悬架系统提供了帮助，对其在非结构环境下行进保持稳定性有着非常重要的作用，也有助于评价移动平台有关的结构参数，能够帮助选择最优调节器的控制方法及控制器的设计。

[1] 张效祖.工业机器人的现状与发展趋势[J].世界制造技术与装备市场, 2004,(5): 1-3.

[2] 杨玉维, 张明路.6自由度轮式悬架柔性单杆移动机械手动力学研究与仿真[J].机械设计, 2009(10): 26-10.

[3] 余志生.汽车理论[M].北京: 机械工业出版社, 2009.3.

[4] 向 博, 高丙团.非连续系统的Simulink仿真方法研究[J].系统仿真学报, 2006, 18(7): 1750-1754.

[5] 王延娟, 杨雪.JTG B01-2003与JTG B01-1997 公路工程技术标准的车型换算方法研究[J].交通标准化, 2006(10):31-34.

[6] Mohamed Bouazara, Marc J.Richard, An optimization method designed to improve 3-D vehicle comfort and road holding capability through the use of active and semi-active suspensions, Eur.J.Mech.A/Solids, 2001(20): 509-520.

[7] Keum-Shik Hong, Dong-Seop Jeon and Wan-Suk Yoo, A new model and an optimal pole-placement control of the Macpherson suspension system, SaeTechnical Paper Series,1999-01-1331.

[8] 周长锋.铰链式自卸车悬架系统动力学建模与仿真[J].汽车技术, 2004(9): 15-18.

[9] 林茂成, 赵济海.GB7031-1987车辆振动输入—路面不平度表示方法[Z].北京: 中国标准出版社, 1987.