基于Adams的传动轴的柔性分析

赵高飞，孙小进，裴云天

（中国科学院 上海技术物理研究所，上海 200083）

0 引言

近几十年来，伴随着微电子技术和计算机技术的飞速发展，伺服系统得到了越来越广泛的应用。如今它的应用已经几乎遍及了社会的各个领域。一般的伺服系统，都是由电子学系统和机械系统构成。电子学系统用于检测、处理和放大信号，最后通过执行机构如直流或交流电机带动机械负载，实现给定的速度、位置和运动轨迹等的控制。在普通的应用场合，对电气系统进行设计时，一般都将机械系统视为刚性系统，即认为机械系统的刚性无限大，可以精确实现电子学系统指定的任何运动。然而实际上任何机械系统，其刚度都是有限的。在一般对系统精度和响应速度要求不高的应用情况，对机械系统的这种近似处理是可行且合理的，对系统影响很小且可以大大简化实际的工程问题。然而在一些高性能的应用场合如航天仪器扫描系统的运动控制，由于系统的控制精度以及快速响应等要求，机械系统的柔性不能忽略。为此，本文对简化的电机-负载系统进行了研究，分析了机械系统柔性对伺服系统性能的影响。并针对实际问题，使用广泛使用的多体分析软件Adams对航天仪器扫描系统中的一根转轴进行了刚柔混合分析，研究了其柔性所造成的影响。

1 抽象的简化模型

为研究机械系统柔性的影响，考虑一个抽象的简化模型，如图1所示，电机通过一个扭簧带动负载进行运动。电机的转动惯量为JM，负载的转动惯量为JL。扭簧的扭转刚度为Ks，模拟了电机和负载之间机械系统的刚度，Ks越大，刚度越好；扭簧阻尼为Bs，用于模拟机械系统的阻尼，即电机和负载发生相对运动时所产生的正比于相对速度的粘滞力的作用。

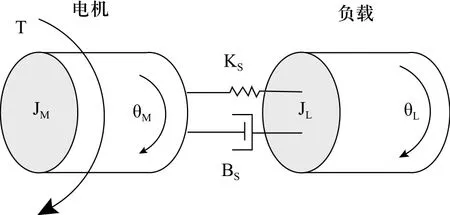
图1 抽象的简化模型示意图

使用控制领域广泛应用的方框图对该系统进行建模，得到其系统框图如图2所示[1]。

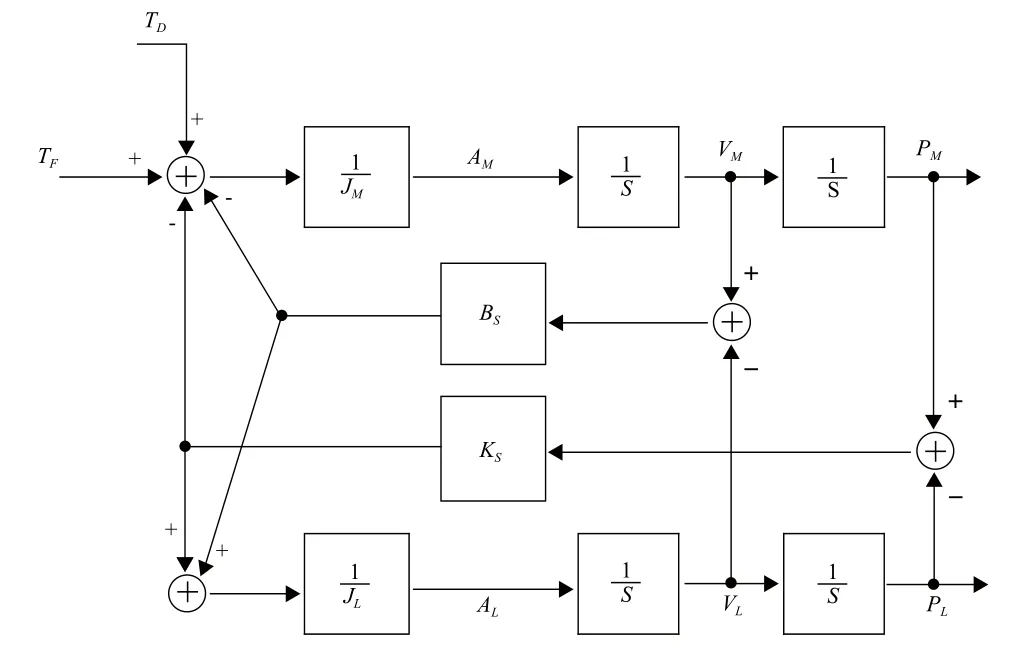
图2 简化模型的系统框图

图中AM，VM，PM分别代表电机的角加速度、角速度和角位移，AL，VL，PL分别代表负载的角加速度、角速度和角位移，TF为输入力矩，TD为干扰力矩，S是频域内的复变量。

由此可计算出负载角位移输出相对于电机输入力矩的传递函数为[1,2]：

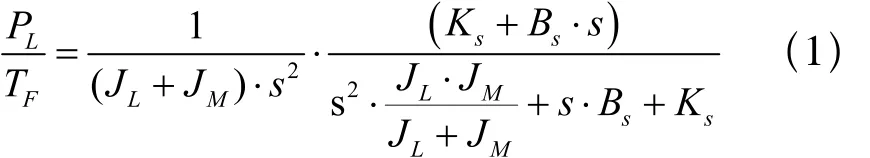
对于刚性系统，刚度Ks和阻尼Bs无限大，则(1)式的第二项为1，剩下的第一项即为刚性耦合项。由此，第二项为柔性耦合项，是因为机械系统具有有限的刚度和阻尼而引起的。

同样，电机的角位移输出相对于电机输入力矩的传递函数为：

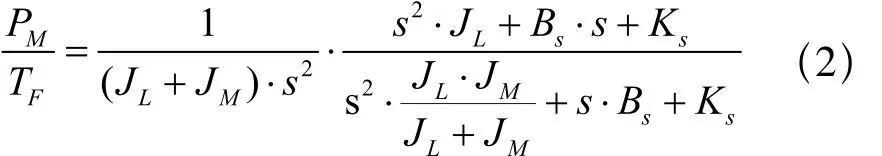
(2)式的第一项与(1)式的第一项相同，为刚性耦合项，第二项为柔性耦合项。

对式(1)、(2)两式的第二项进行分析可以发现，当s--＞0即低频状态下，两项均趋近于1，系统表现出刚性耦合的特点。因此对于响应性能要求不高即驱动频率很低的应用场合，将机械系统简化为刚性系统影响不大。

一般的二阶系统，其传递函数(输出C比输入R)的标准形式为[3]：

将(1)式按(3)式的格式改写为：

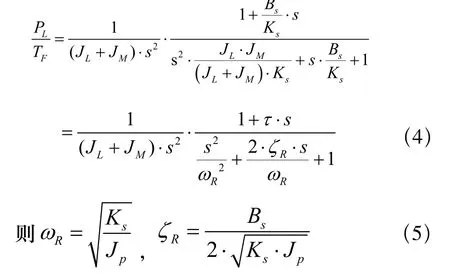
同样可以将(2)式按(3)式的格式改写为：

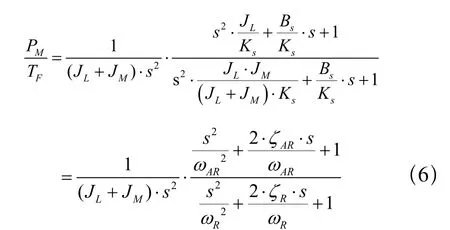
在Adams中可以很容易地对这个系统进行仿真。如图3所示建立这个简化问题的多体动力学模型，其中右边的小圆柱体代表电机，其转动惯量取为10kg·mm2，左边的大圆柱体代表负载，其转动惯量取为100kg·mm2。电机通过一根扭簧驱动负载运动，扭簧的扭转刚度为1000N·mm/rad，阻尼为1N·mm·sec/rad。根据(7)式，反共振频率为100rad/s，即15.9Hz。共振频率为331.7rad/s，即52.8Hz。

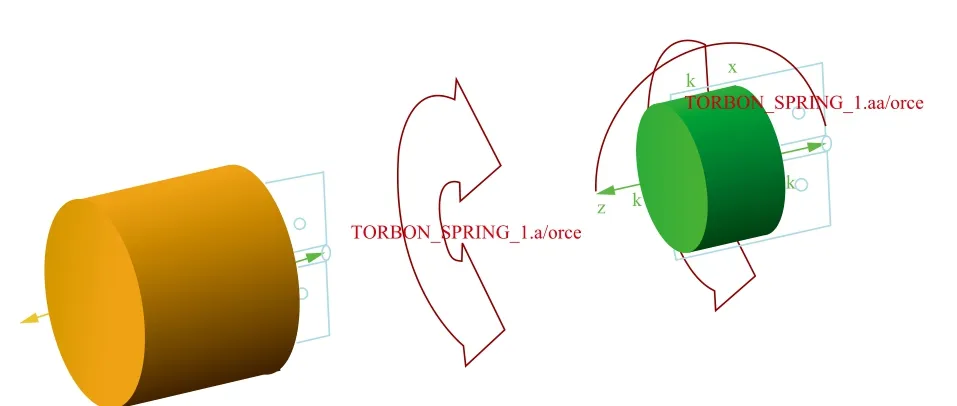
图3 简化问题的多体动力学模型

利用Adams的Vibration模块进行仿真，在电机位置施加1～1000Hz的扫频力矩激励，并在电机和负载位置建立输出通道，测量电机和负载的角位移的幅值和相位，得到传递函数曲线如图4所示，在图中可以测量出系统的反共振频率为15.9Hz，共振频率为52Hz，与理论计算值是非常一致的。

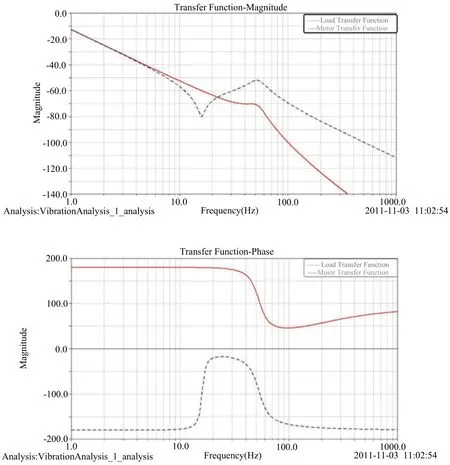
图4 电机和负载的角位移相对于力矩输入的传递函数

理论上如果机械系统是刚性的，则无论电机还是负载，其角位移输出相对于力矩输入的幅频特性曲线都应该是一条以-40dB下降的曲线。但由于机械系统的柔性，由图4的分析结果可以看到对于电机而言，在反共振频率附近电机转角开始明显偏离-40dB直线，直到共振频率之后才恢复正常。对负载而言在共振频率附近负载转角开始偏离-40dB直线，而在共振频率点之后的很长一段频率范围，负载都与刚性连接的情形有较大的偏差，振动幅值下降并且存在一个相位延迟。

2 实际的机械系统

考虑一个更实际的模型，在某航天仪器中电机通过一根轴带动扫描镜进行转动。由于仪器对扫描镜的控制精度以及响应性能等要求很高，需要将转轴的柔性考虑进去。为此，需要对轴进行柔性化处理。

在Adams中，复杂部件的柔性化一般是通过在其他有限元软件(如Ansys，Nastran等)生成模态中性文件(MNF，Modal Neutral File)再导入到Adams软件，通过模态叠加法来计算部件与其他部件作用时所产生的变形[4,5]。图5是指向系统中的水平电机轴在Adams中的前几阶模态振形，由于在Natran中取了10阶模态，而轴与其他部件作用的外节点有三个，因此在Adams中总共有34(6+10+3×6)阶模态。

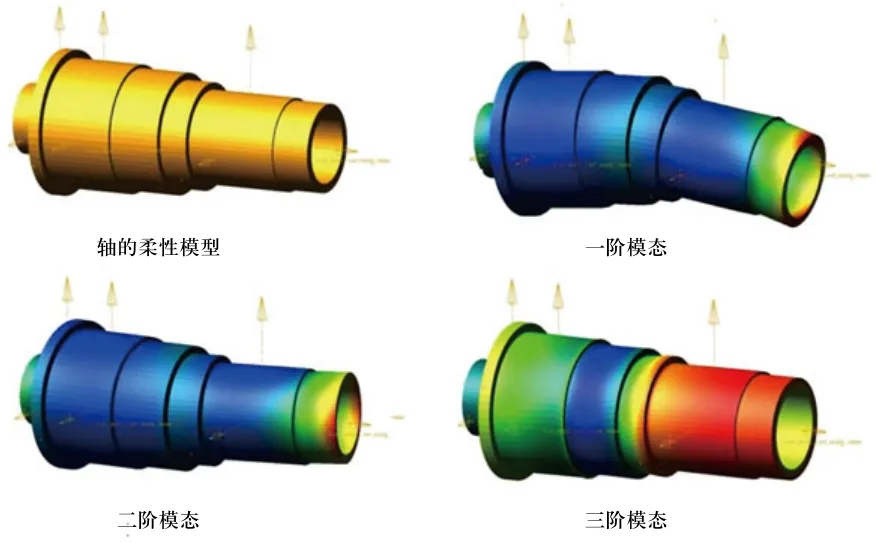
图5 电机轴的模态图

轴的柔性模型建立好之后，在Adams中加入电机和负载，并施加必要的约束，建立系统的刚柔混合动力学模型，如图6所示。

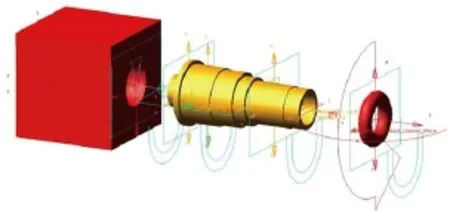
图6 实际轴传动的多柔体动力学模型

图中大的方块代表负载，根据实际系统，其转动惯量为1.48X106kg·mm2。负载通过固定铰链固接到电机轴上；圆环代表电机转子，其转动惯量为140kg·mm2，也通过固定铰链连接到电机轴上。整个电机轴在安装轴承的位置通过一个转动副连接到支架上。因此整个系统只有绕电机轴转动的一个刚体自由度。在Adams中，利用Vibration模块进行仿真，在电机位置施加10～20000Hz的扫频驱动力矩。同时，在电机和负载位置，分别建立输出通道，测量电机和负载位置的角位移幅值和相位，研究其随驱动频率的变化情况，得到传递函数的幅频和相频曲线如图7所示。

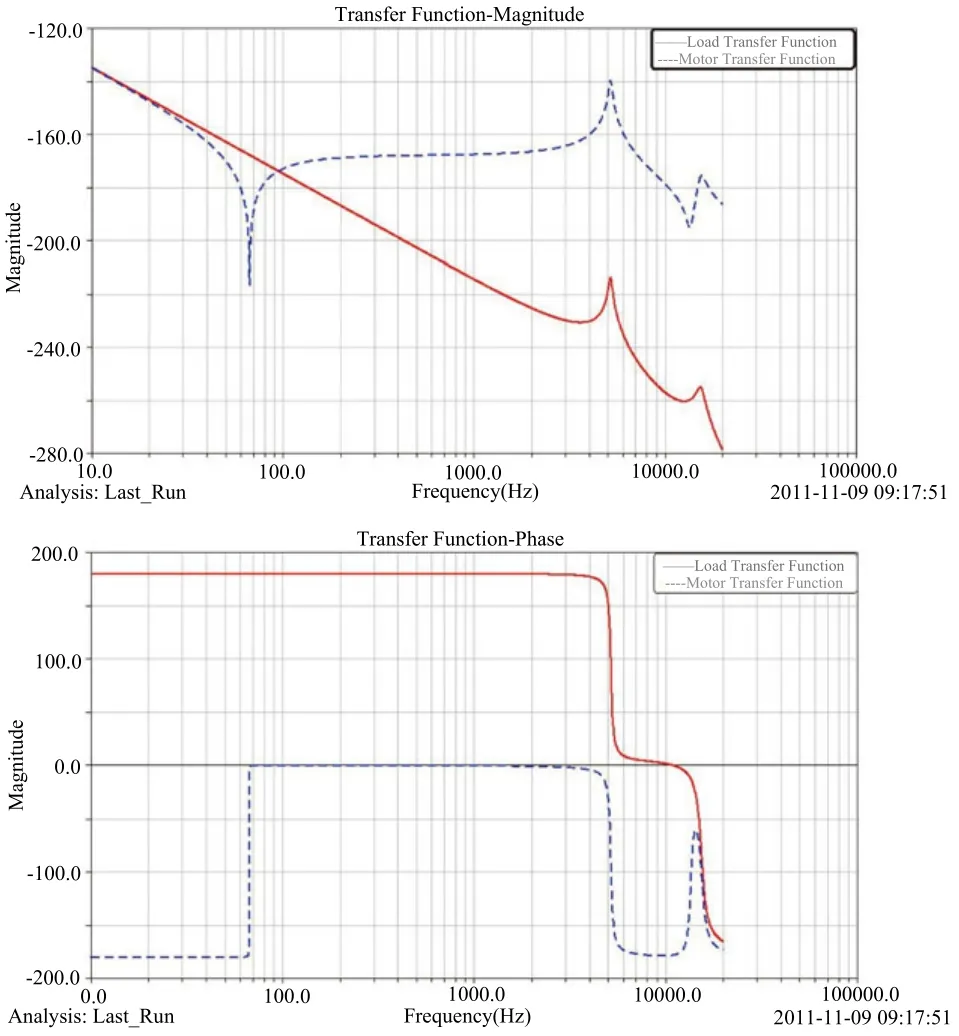
图7 10～20000Hz实际系统的传递函数

仔细研究图7中实际模型的幅频和相频曲线，可以发现在83Hz左右存在一个反共振频率，电机的角位移传递函数明显偏离-40dB直线，出现一个向下的尖峰；在5169.5Hz左右存在一个共振频率，负载和电机的角位移传递函数幅值都出现一个向上的峰值。与图4中简化的抽象模型进行对比，可以发现图7实际模型负载和电机的角位移传递函数曲线与抽象模型是非常类似的。这充分说明了抽象化的模型概括出了实际机械系统的本质。实际的机械系统，在控制环节上表现出来的就是一定的刚度和阻尼，从这个角度看它和一根具有一定刚度和阻尼的扭簧没有本质上的区别。实际上，由于电机轴有很多模态，相当于其等效的“扭转刚度”并非只有一个，如果继续将扫频的范围扩大，我们可以发现，电机和负载的传递函数曲线上还将出现反共振和共振的峰值，如图8所示。

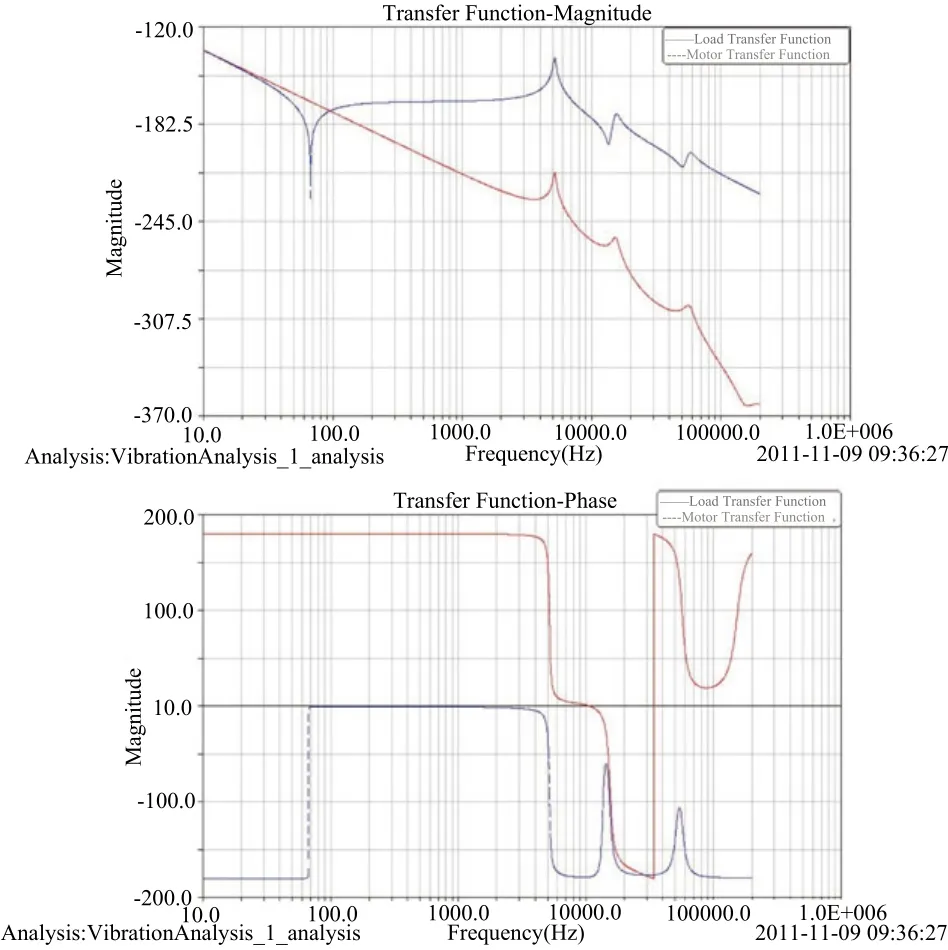
图8 10～200000Hz频率范围内实际系统的传递函数

3 反共振频率的本质

由上面的分析我们可以看出，由于相对于负载的转动惯量，电机自身的转动惯量一般都很小，因此由(5)式和(7)式我们可以看出共振频率一般都很高，远远高于反共振频率，在低频段，限制系统带宽的主要是反共振频率。

反共振频率的产生实际上可以从系统内部的能量交换的角度来理解。当我们保持驱动力矩的大小不变，只是改变驱动力矩的频率时，我们发现在低频段，即力矩方向非常缓慢时，电机还能非常精确而稳定地通过传动轴带动负载进行运动。当频率慢慢升高，电机的相位将慢慢滞后，振动的幅度也慢慢下降。到了反共振频率段，电机角位移的相位从-180°变成了0°，几乎与原来的相位完全相反了，振动幅度也达到最小。此时，驱动力矩的频率处于这样一个状态，即虽然它实际是作用在电机上，但由于其频率与机械系统的反共振频率一致，它的能量转换成电机动能的部分很少，大部分能量被柔性的传动轴吸收并传递给了负载。

图9 角位移激励时负载和电机处的传递函数

反共振频率的产生实际上也跟控制的输入有关。如果控制的输入量是电机处的力矩，则在反共振频率点，会出现上述电机不动而负载运动的情况。如果控制的输入量是电机的角位移，即控制电机的转角按给定频率做简谐振动，则系统呈现的规律将截然不同。在Adams中将输入激励换成1～1000Hz的角位移激励，同样地测量负载处的角位移传递函数，如图9所示。

由图9的传递函数曲线可以看出，在低频段负载还能与电机做同步运动。而到了在图7的反共振频率点(83Hz)，负载的角位移出现了一个峰值，产生了激振。负载转角相对于电机的转角放大了几十倍，具体的放大倍数与电机轴的阻尼有关，阻尼越小，转角放大得越厉害。由此可见，反共振频率就是开环控制时的共振频率。对于开环系统，在没有使用传感器测量负载的角度进而通过负载角度对电机进行负反馈控制时，共振的情况是有可能发生的，这是设计系统时需要注意和考虑的。

4 结论

本文先分析了一个简化的抽象模型，通过建立框图进行理论分析并在多体分析软件Adams中进行建模，研究了机械系统存在柔性时传递函数的特性，得到了力矩激励时共振和反共振频率的表达式。然后通过在Adams中对实际航天仪器中的一根传动轴进行多柔体动力学分析，研究了实际机械系统的柔性对输入输出的影响，得到了其共振和反共振频率，证明理论分析的正确性。通过改变输入的激励方式，分析指出了力矩输入时的反共振频率就是开环控制系统的共振频率。对于开环系统，在该共振频率点，负载将产生激振，失去控制。在实际的伺服系统设计时，需要充分考虑机械系统的柔性所带来的影响。

[1] George Ellis, Robert D.Lorenz.Resonant Load Control Methods for Industrial Servo Drives[J].IEEE Industry Applications Society Annual Meeting.2000.10.

[2] 吴恒.基于SOPC的高精度扫描控制技术研究[D].中科院上海技术物理研究所.2009: 46-50

[3] 竺长安, 张屹.控制理论与机械系统控制[M].高等教育出版社.2003: 36-40

[4] 李增刚.Adams入门详解与实例[M].国防工业出版社.2006: 125-154

[5] Adams-Online Help & Adams-Release Notes