论风力发电双馈机组的变速仿真研究

史 毅

（江西现代职业技术学院 机械学院，南昌 330029）

0 引言

纵观世界范围，能源形势不容乐观，煤炭资源日渐匮乏，石油价格的不断攀升，一方面可以看出全球对于能源的竞争日益激烈，另一个方面也看出能源在人们大范围的使用中在不断地减少，如何在不破坏地球原有的生态环境又能满足人们日益增长的物质要求已经摆在人们的面前，是一个非常普遍又现实的存在，而风能能很好地解决上述的两个矛盾点，不仅资源存储丰富，又能循环利用，同时在各国科学家的努力之下，风能生电的技术应势而生，在全球范围内得到了很好的应用，性价比也非常的高，可以采用很少的资源满足全球范围内人们的日常用电量，避免了对环境的污染，保护了生态，是一种非常实用的技术。

风能发电就是利用风轮收集风能，将其转变为旋转的机械能，通过发电机将风轮收集的机械能转变成电能，利用电网远距离输送。风力发电是由太阳能转化而来，地球表面温差引起空气流动，具有一定动能，是清洁的、无污染的、取之不尽用之不竭的可再生能源。由于能源和环境等诸多问题的影响，风力发电的发展受到全球性的广泛关注和高度重视。但是自然界的风，方向和速度经常变化，使得风力发电具有间歇性，可控性不如常规性能源。

1 双馈发电机组原理

风力发电就是利用风力带动风车叶片进行旋转，再通过齿轮箱将旋转的速度进行进一步地提升，故而带动发电机达到发电的目的。风力发电系统主要由叶轮，机舱，偏航系统，传动链，主轴，发电机，制动系统和桨距调节装置等硬件设备组成，每一个部分都很重要。其中，叶片是具有空气动力学外形，在气流推动下产生力矩使风轮绕其轴转动的主要原件，获取风能并转化为机械能。齿轮箱是将风轮转速在高速轴侧提高到满足发电机需要的转速。而发电机组在风力发电系统中至关重要，目前在风力发电领域广泛应用的风力发电机组主要有三种类型，即固定转速的异步发电机组、可调速的双馈异步发电机组和永磁直驱同步发电机组。

双馈电机发电的主要原理就是利用变频器调节转子，然后通过励磁电流来达到控制变速时候的频率，使之保持在一定的频率上。在这个过程中，转子电路的功率只相当于流励磁电机发电中的转差功率，而转差功率在整个过程中只占到很小的一部分，所以双馈电机在进行运转时消耗功率较小，降低了成本，同时不限制变频器容量，故采用双馈电机。在进行发电时，不但可以减低能耗，保证工作，同时在工作中创造效率，实现恒频控制，且同时实现一对一的控制，起到了分担电网工作量，稳定电压的效果。风力机的运行特性如图1所示。第一个运行区域是启动阶段，此时电机增速，但没有连接并网，故没有功率输出。第二个运行区域是风力发电机并入电网并运行在额定风速以下的区域。这一阶段又可分为两个区域：变速运行区和恒速运行区。第三个运行区域为功率恒定区。当风速增加时，通过变桨控制，从而保持功率不变。

图 1 风力机的运行特性图

2 双馈电动机变速仿真

影响风能发电的因素有很多，其中风能的输入功率，叶片的叶尖线速度都与之有着千丝万缕的关系，如何更好地捕获风能，提高风能的效率，同时减小机械应力，是目前迫切需要解决低问题。

根据上述风力发电的基本原理，加上风力机的空气动力学知，可以得出风力机的输入功率为：

由于通过风轮旋转面的风能不能全部都能被风轮吸收利用，其风能利用系数：

其中，v为风速，ρ为空气密度，R为叶片半径。

风能利用系数是表征风力机效率的重要参数，它与风速、叶片转速、叶片直径、桨叶节距角均有关系。为了便于讨论，定义风力机的另一个重要参数叶尖速比，即叶片的叶尖线速度与风速之比：

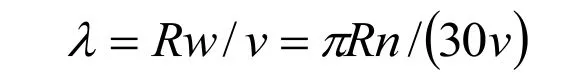
由不同风速下风力机输出功率和转速的关系，可以看到不同风速下风力机的功率转速曲线组成了曲线簇，每条曲线上最大功率点成为风力机的最佳功率曲线。风力机运行在Popt曲线上将会输出最大功率Pmax其值为：

同时以双馈风力发电机组的电机模型建模，以转速ωee旋转的同步坐标系下的等效电路如图2所示。

图2 等效电路图

根据原理对双馈风力发电机组的电机模型进行建模，得到磁链和电压的数学模型如下：

式中，ψ、V、I分别为磁链、电压、电流矢量，R、L为电阻及电感，下标s、r分别表示定、转子侧分量，ωr为转子角速度，Lm为激磁电感。

同时当采用定子磁链定向（即同步坐标系的d轴定向在定子磁链矢量上）时，定子侧的有功和无功可表示为：

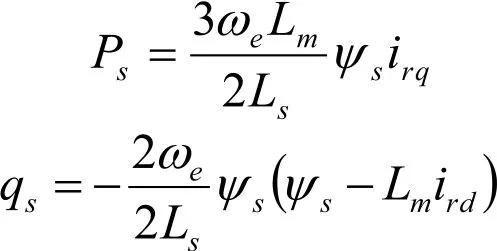
且此时的电磁功率和电磁转矩可以表示为：

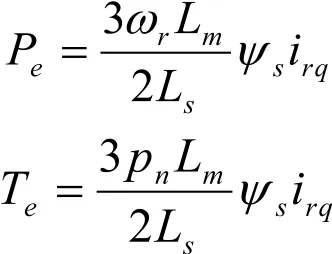
由上面的几个公式中可以看出双馈电机的定子侧有功（或电磁转矩）、定子侧无功分别由转子电流的q、d轴分量决定。

以16m/s风速条件下风机模型为被控对象进行仿真。由于风轮为一大惯性体，控制延时大，因此要求在控制超调量条件下响应时间越短越好。风机模型中发电机额定转速为1500rpm，最高转速为1800rpm，其最大超调量为20%，为减少干扰信号带来的误差，本文设定最大超调量为10%。根据MATLAB中SIMULINK仿真模块，建立如图3所示的仿真模型图。

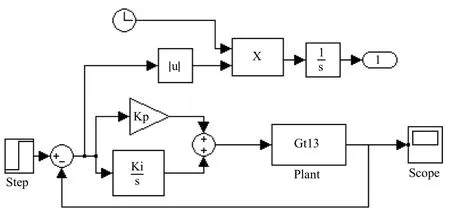
图3 实验仿真图

在本文中选取参数相同的规格的一组电动机进行仿真比较，在使用过程中，通过改变某些特定参数来进行比较，得到了结果如表1所示的实验数据。

表1 仿真比较数值结果

如表1所示，电机组2的电动机最大超调量虽然比最优控制提高3%，但响应时间多了40.1%，在风力发电机组，电机组1这样大惯性系统中起到更好控制效果。电机组2的电动机的转子电流的q轴值值比较偏高，故相对于无功的需要量比较大，而电机组1相对于偏低，故整个动态过去需要量比较小，是可以控制的

同时从上面的分析也可以得到，在某一固定的风速v下，随着风力机转速的变化，风能利用高，从而使风力机输出的机械功率也越大，因此转速的变化会导致风力机捕获风能的能力却强，故电机组1的相应时间小于电机组2的电动机，确实是提高了风能转换效率。

3 结束语

随着二十一世纪的到来，各国对于资源的争夺越来越激烈，而风能作为一种存储丰富，对于环境的破坏相对较小的能源，成为了各国争先研究的对象。现在在全球范围内正形成一股应用风能进行发电的研究热潮，可靠风能不仅能降低污染，还不必担心资源的枯竭，是一种可以循环利用的能源，当然在发展过程中也存在着不可以忽视的缺点，造成一些不必要的浪费，针对上述的情况，本文对于风能发电的双馈电动机进行了研究，阐述其原理，且通过选取几个有针对性的对比实验参数，更从数值证明了本文提出的合理控制双馈发电机组的变速的参数确实有比较高的实用价值。

[1] 迟永宁, 刘燕华, 王伟胜, 等.风电接入对电力系统的影响[J].电网技术, 2007, (2).

[2] 赵洪杰, 马春宁.风力发电的发展状况与发展趋势[J].水利科技与经济, 2006, (9).

[3] 孙涛, 王伟胜, 戴慧珠, 等.风力发电引起的电压波动和闪变[J].电网技术, 2003, (12).

[4] 范伟, 赵书强.风电场接入电网强迫功率振荡研究[J].东北电力技术, 2009, (1).

[5] 张步涵, 曾杰, 毛承雄, 等.电池储能系统在改善并网风电场电能质量和稳定性中的应用[J].电网技术, 2006, (8).